基于APOS理论的初中数学概念教学的设计初探

张衡

【摘 要】  为探究APOS理论的教学设计在数学教育中的应用，本文以"一次函数"单元为例，从行动、过程、对象、图式四个阶段的进行数学概念的教学设计，帮助提高初中学生对数学概念的理解和掌握程度.

【关键词】  APOS理论；一次函数；数学概念；教学设计

数学教学一直以来都是一个需要不断创新和改进的领域[1].随着教育理论的不断发展，越来越多的教学方法和原理被提出和运用到实际教学中.其中，APOS理论作为一种理论框架，为教学设计提供了新的思路和方法[2].APOS是指 Action，Process，Object，Schema（行动、过程、对象、图式）四个阶段，描述了学习数学概念的过程.本文以初中数学中的"一次函数"单元为例，探讨了基于APOS理论的概念教学设计，旨在帮助学生深入理解和掌握一次函数的概念、性质和应用.

1  “一次函数”概念的教学设计

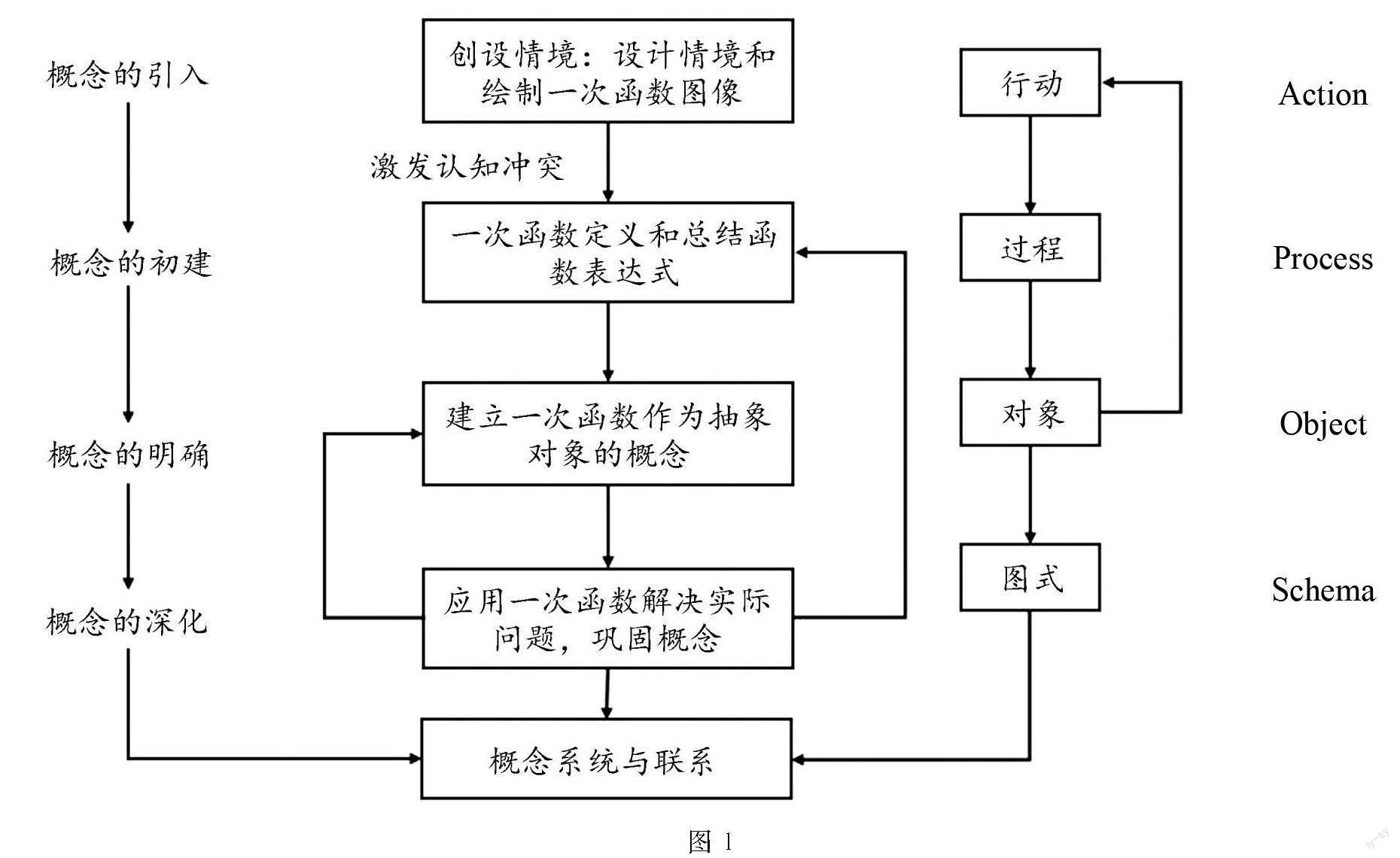
基于APOS理论对该单元进行概念教学设计的探究流程如下图1所示.

图1

2.1  行动阶段-创设情境感知概念

在第一个阶段可以通过引导学生通过直观的操作和实际的例子，感知一次函数的特征和性质，引发学生对一次函数的兴趣和思考.

情境引入  如图2，如果我们知道一个物体A从一个位置出发，以一定的速度匀速向右运动，我们能否根据时间来确定物体的位置呢？

图2

教师：在上述情境中，哪个量是固定不变的？哪个量是变化的？

学生1：因为是匀速行动，则速度是不变的.

学生2：变量是时间，时间在变化.

教师：行驶的距离和时间构建函数为，当这里的速度=80m/min，你能求出=10min，t2=20min时物体运动的距离吗？请分别列出他们的表达式.

学生3：S1=·=8010=800m，S2=·=8020=1600m.

教师：引入一次函数的概念，一次函数表示了两个变量之间的线性关系.其中，t是自变量，s是因变量.当t增加或减少时，s的值也按照一定的比例增加或减少.

实际操作  将学生分为几个小组，让他们按照图3将木板垫起来至不同高度，观察小球的运动速度，小球到达底端的时间.

图3

学生4：模板越高越斜，小球运动得越快，到达木板底部的距离越短.

教师：一次函数的代数表示形式是y=mx+b，其中m是斜率，b是截距.通过这个实验我们可以知道斜坡倾斜程度和小球下滑速度之间的关系，可以很好的理解斜率这个特性.那么对于截距该如何理解？

学生5：表示当自变量为0的时候，起始的情况.

教师：设计一个人走的距离实验.学生可以使用不同的起始位置开始行走，并测量记录每个位置对应的步数和距离.教师：展示一次函数图像如图4.让学生思考一次函数图像特性以及一次函数的基本概念.

图4

设计意图：通过直观的操作和实际的例子，学生可以更好地感知一次函数的特征和性质，从而对其有更深刻的理解.

2.2  过程阶段-解决问题初建概念

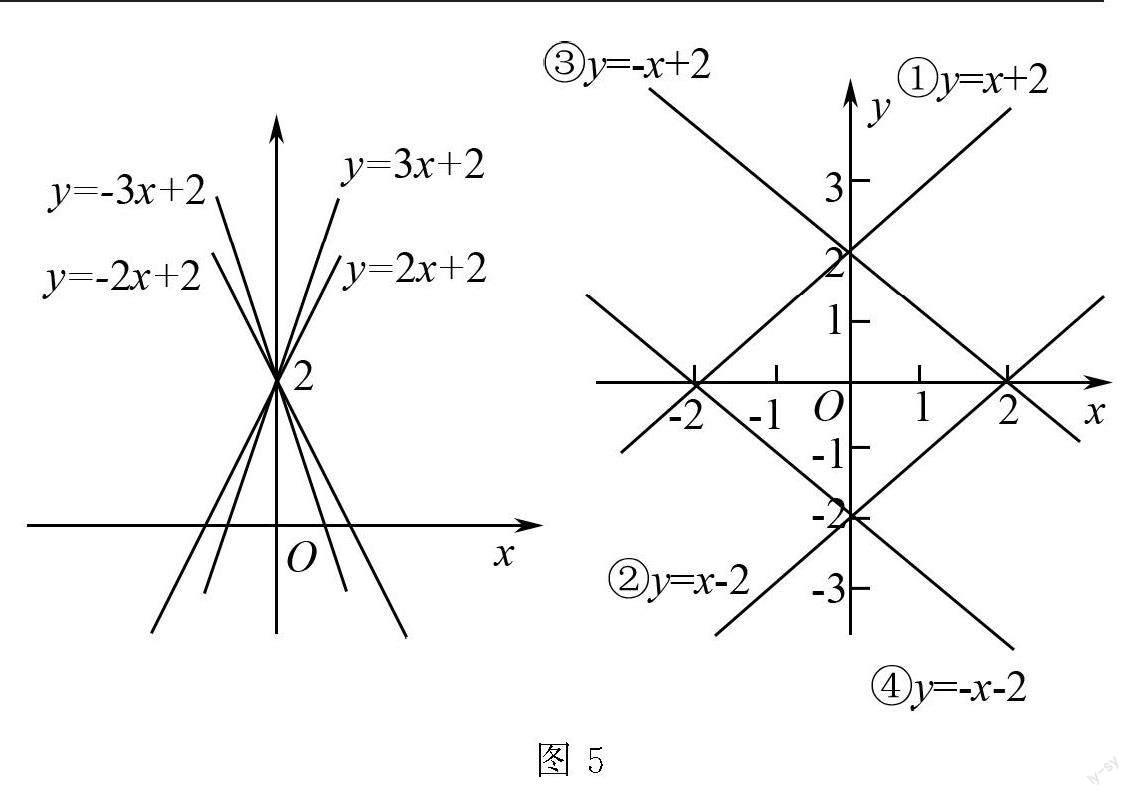
探究过程  教师向学生展示不同斜率和截距的直线函数如图5.

图5

教师：对图像对应的直线进行讲解，让学生观察和分析一次函数的图像特征，引导他们发现斜率、截距和图像形状之间的关系.

学生6：斜率表示直线的倾斜程度或者斜率的大小.

学生7：当斜率为正数时，直线向上倾斜.这表示随着自变量x的增加，因变量y的值也会增加.斜率越大，变化越陡峭.

学生8：当斜率为负数时，直线向下倾斜.这表示随着自变量x的增加，因变量y的值会减少.斜率越小（即绝对值越大），变化越陡峭.

教师：斜率和截距是直线性质中重要的参数，它们决定了直线的斜率、倾斜方向、位置和平移.

解决问题  玛丽买了一些苹果，她每天吃掉的苹果数量和剩余的苹果数量之间存在一种线性关系.已知第一天剩下10个苹果，经过5天后，剩下2个苹果.利用一次函数来解决经过6天后，预计还剩下几个苹果？

学生9：假设函数的自变量为天数（x），因变量为剩余苹果数量（y）.通过题意可以得到两对坐标点：（1，10）和（5，2），得一次函数为

学生10：将x=6，代入一次函数中，y=0，则预计剩下0个苹果.

教师：根据这个实例，学生将一次函数运用其中，对一次函数的概念、性质以及应用更加理解.

3  反思感悟

在这个教学设计中，需要注重设计了各种互动和探究活动，通过让学生积极参与掌握知识，可以激发他们的兴趣和动力.并强调将新的数学概念与学生已有的知识和经验进行连接，可以帮助学生更容易地理解和接受新的概念.使用图表、方程、實例等来表达和解决一次函数的问题学生灵活地在不同的表征形式中转换和应用知识，可以促进他们对概念的深入理解.

参考文献：

[1]彭小烜.基于APOS理论的初中数学概念教学优质课的特征研究[D].重庆三峡学院，2023.

[2]王悦，马旭.APOS理论指导下的初中数学概念课教学——以“直线、射线和线段”为例[J].数学教学通讯，2023（14）：10-13.