深研细究 实现教学至简

于淼红

摘 要：好的试题往往具有良好的教学导向作用，教师应挖掘典型好题的育人功能，盘活好题资源，开发试题的教学功效，拓宽学生的思考视角，提高教学效能，使学生将知识融会贯通，轻松地学数学，实现教学至简.

关键词：至简教学；转化思想；解题教学

1 深研课标，细品教材

数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构，是实现数学课程目标、实施数学教学的重要资源.在教学设计之前，教师应该认真研读课程标准，深入研读教材，揣摩教材编写意图，体会教材如何承载课程目标，过程中不仅要关注數学知识本身，而且要思考知识背后蕴含的数学本质，包括数学知识的内在联系、数学规律的形成过程、数学思想方法的提炼和数学理性精神的体验.在此基础上，灵活地、创造性地使用教材.本节课意图在深入理解教材的基础上用教材进行教学.

例题：（人教版八上62页习题） 在△ABC中，AD为角平分线，∠ABC＝2∠ACB，求证：AB+BD=AC.

2 在情境引学中将思维由浅表引向深入

数学是一门训练思维，提升能力的学科.“解法开放”是全国各地历年中考数学压轴题的特色之一.但只要认真探索这些数学试题，均能发现隐藏其中的“共性”，即试题大都回归数学本源，注重通性通法，凸显数学能力的考察.

方法探究一（核心思想一：转换，造等角——出等腰）

在平面几何中，相等的角有着重要价值，相等的角可以联想到等腰三角形，可以联想到角平分线，可以构造全等，可以构造相似等.二倍角问题又是平面几何中的一个常见问题，也是一个难点问题，所以当二倍角出现时我们可以把二倍角转化成相等的角，利用相等的角去解决问题.

已知条件∠ABC＝2∠ACB是解题的关键.现在我们来研究一下，如何处理二倍角问题.

方法1：延等腰：延长CB至D，使得BD＝AB，可以得到∠D＝∠C＝∠BAD，通过这组等角我们得到两个等腰三角形和一个斜A相似.

方法2：截等腰：在BC边上取点D，连接AD，使得AD＝CD，得到∠C＝∠CAD，∠B＝∠ADB，这样通过这组等角我们可以得到两个等腰三角形.

方法3：作角平分线：做△ABC的角平分线BD，得到∠CBD＝∠C＝∠ABD，通过这组等角我们得到一个等腰三角形，一个角平分线，一个斜A相似.

方法4：翻折：把直线CB沿AC翻折得到直线CD，设CD交BA延长线于D，得到∠B＝∠BCD，∠ACB＝∠ACD，这样通过这组等角我们可以得到一个等腰三角形和一个角平分线.

总结：关于二倍角问题，上面介绍了四种添加辅助线的方法，主要目的都是为了构造相等的角，进而推出角平分线、等腰三角形等，然后再利用相关的性质探求解题途径.由于种种原因，学生的思维往往处于沉睡状态.数学教学中，教师要努力寻求问题之间的连接点、生长点，循序渐进，形成自然联系的整体，为思考铺路，为探究引航，不断唤醒和激活思维，引导学生进行深度学习，让学生建立“属于自己”的知识结构、思维方式和学习经验.

例题赏析

例1 在△ABC中，AD为角平分线，∠ABC＝2∠ACB，求证：AB+BD=AC.

方法1：延等腰：如图7，延长AB至E，BE＝BD，连接DE，△ADE≌△ADC，AE＝AC，所以AC＝AB +BD.

方法2：截等腰：在AC边上截取AE＝AB，则△ABD≌△AED，易得BD＝DE＝CE，所以AC＝AB + BD.

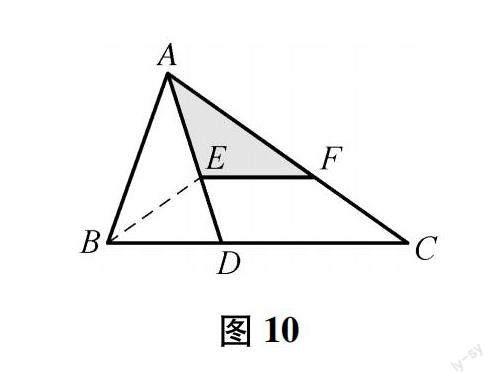
方法3：作角平分线：过B做BE平分∠ABC交AD于E，EF平行BC交AC于F，导角得BD＝BE，易证△ABE≌△AFE，所以AB＝AF，易得CF＝BE，所以AC＝AB+BD.

方法4：翻折：把直线CB沿AC翻折得到直线CE，AE∥BC，得到∠ABC＝∠BCE，∠ACB＝∠ACE，易得AB＝CE＝AE，在AC上取点F，在AD上取点G，使得AF＝AE、BG＝BD，△BGA≌△CFE，所以BD＝BG＝CF，所以AC＝AB+BD.

通过这一道教材习题，聚焦基本图形，深入引导学生挖掘基本图形中隐含的数学知识.这一过程在学生数学现实的基础上，利用问题引导学生感受发现数学知识的过程，通过从特殊到一般、从具体到抽象的引导过程激发学生深度思考，促进高阶思维的发生.

3 探究研学，激发思维

专题探究课应注重层层深入、揭示问题的本质，促进学生思维深入发展.苏联教育家霍姆林斯基说：“只有让学生在认知过程中感受自己的智力，体会到创造的愉快，才能激发学生高昂持久的兴趣.”本节课通过有效设置问题变化情境，精心设计探究过程，有效组织探究活动，引导学生科学有序地对模型本质进行探究.

例2 如图12，在△ABC中，∠B＝2∠C，求线段AB、BD与CD的数量关系.

方法1：延等腰：延长CB至E，使得BE＝AB，得到∠E＝∠C＝∠BAE，易得DE＝CD，所以AB+BD＝CD.

方法2：截等腰：在BC边上取点E，连接AE，使得AE＝CE，得到∠C＝∠CAE，∠B＝∠AEB，所以BD＝DE，AB＝AE＝CE，所以AB+BD＝CD.

方法3：作角平分线：过B做BE平分∠ABD交AD于E，EF∥BC交AC于F，在线段AF上取点G，AE＝EG，可证△BDE≌△CHF，△ABE≌△EFG，所以BD＝CH，AB＝EF＝DH，所以CD＝AB+BD.

方法4：翻折：把直线CB沿AC翻折得到直线CE，AE∥BC，得到∠B＝∠BCE， ∠ACB＝∠ACE，易得BD＝CF，AB＝DF，所以CD＝AB+BD.

高阶思维的发生需要问题的驱动.如何从学生的数学现实出发设置问题，开展有效的思维活动？如何通过问题引导，让学生在解决问题的过程中感悟数学思想方法？如何让学生体会到习题课中的思维升华，通过类比、拓展实现思维创造，生成数学知识，积累基本经验，基于以上思考，本节课的问题引导从特殊到一般，从方法类比到图形构造.在问题引导中溯源问题本质，在思想方法的感悟中探求新知，让学生经历知识的形成、巩固和深化的过程.

方法探究二：（核心思想二：导特殊）

有一些二倍角的问题中往往隐藏了某种特殊，可以是隐藏特殊三角形，特殊角，特殊关系，需要我们导角把特殊找到，然后根据特殊解决问题.

例题赏析

例3 如图17，在△ABC中，AD为高线，BD＝2，CD＝3，∠BAD＝2∠C，求线段AD的长度.

解析：如图，设∠ACB＝x，则∠BAD＝2x，∠CAD＝90°-x，∠BAC＝90°+x，导出AC为△ABD的外角平分线，所以过C做CE⊥AB于E，所以CE＝CD＝3，勾股定理得BE＝4，得到∠B的正切值，所以AD＝1.5.

总结：本题就是通过导角得到一个特殊条件：AC为角平分线，然后利用角平分线的相关性质解决问题.

例4 如图19，在△ABC中，D、E分别在AB、AC边上，AD＝CD，∠CDE＝60°，∠ADE＝2∠BCD，BD＝3，DE＝5，求线段CE的长度.

解析：如图设∠BCD＝x，则∠ADE＝2x，∠ACD＝60°-x，∠ABC＝60°+x，所以∠ACB＝60°，得到特殊角∠ACB，延长DE至F，使得DF＝CD，连接CF，在BC边上截取DG＝DB，可证△CFE≌ △CDG，所以BD＝DG＝EF＝3，DE＝5，∠F＝60°，△CEF可得CE＝7.

综上所述，处理二倍角问题的思想主要是：一是造相等，构造出相等的角，利用等角处理问题;二是导特殊，导出特殊关系，利用特殊关系解决问题.

4 培养迁移能力，训练数学思维

学习迁移是指学生在学习过程中把之前学习的知识或解决问题的能力自觉地应用到新知识的学习和实际问题的解决中.通过学习迁移能力的培养，可以有效提升学生的学习效率，优化思维品质，为学生终身发展打好能力基础.

例5 在△ABC中∠C=60°，D、E分别在BC、AC上，AD=AB，AE=EB.

（1） 求证∠ADE=30°.

（2） 点M在CB的延长线上，DM=AE，AM=c，AD=b，DE=a，试确定a、b、c的数量关系.

解析：（1） ［对称法］α，α+60°，60°-2α.

［法1］中垂线GEF，［369△AGF］，两个α，AF＝2AG＝AB＝AD，△AED和△AEF全等［SAS］，两个30°.

［法2］F、B关于AC对称，正△ADF，△ADE和△FDE全等［SSS］，两个30°.

（2） ［等边转换与角度转换］

［法1］∠EBA＝∠EAB＝60°-α，∠ABD＝∠ADB＝60°+α，∠DBE＝2α ∠EDC＝90°-α，作BN＝BE，则DE＝EN＝α，DN＝MB＝n ［美人鱼相似］△NDE∽△NEB［AA］，a²＝n（n+2m）.

［双勾股］c²-b²＝（n+m）²-m²＝n（n+2m），故a²＝c²-b².

［法2］正△AMN，［对顶点O］两个θ，两个黄色三角形全［SAS］正△DNE，Rt△ADN，c²＝a²+b².

5 深度反思，内化思想

反思1：通过本节课可以看出，活动内容只是探究的一个载体，经过探究活动，学生能发现其中的数学本质、找出其中的数学规律，从而带动思维能力的发展.笔者通过对课堂探究教学的尝试与反思，意识到探究教学不是对数学内容的机械重复，而是对数学内容的重置与延伸.

反思2：熟练解题模型，提炼解题规律.解体模型是指教师在解题教学中发现并总结出一些结论性认识，具体指一般化程度较高的结论或图形.G·波利亚认为，解决一个问题之后，要善于去总结一个模型，并井然有序地储备起来，以后才可以随时支取它去解决类似的问题，进而提高自己的解题能力.如本题解决二倍角问题用到的几个基本模型.教师不仅要熟悉一些常见的解题模型，还要在解题教学中指导学生总结提炼解题规律，培养学生良好的解题直觉，启迪学生思考方向，进而顺利解决问题.

反思3： 著名数学教育家弗赖登塔尔曾说过：“与其说让学生学习数学，不如说让学生学习数学化.”意思是学生学习数学的终极目标应该是形成自己的数学思想和方法，学会用数学的眼光去看待事物，学会用数学的方法解决问题.因此我们的教学，不应该仅仅是一节课做完这一题及其变式就了结.我们还应做好梳理总结工作，反思本节课中问题的解决路径、运用的数学知识和思想方法.除了课后反思这一重要环节，教师还需要引导学生在问题解决的核心处深度思考、深切体验数学思想方法的渗透.这便是学生从数学的知识学习走向数学思维化学习的必经之路.

反思4：好的试题往往具有良好的教学导向作用，深研细究试题的内涵并盤活类似的学习资源，能开发试题的教学功效，拓宽学生的思考视角，提高教学效能，使学生将知识融会贯通，轻松地学数学，实现教学至简.

参考文献：

［1］ 王眉燕.渗透数学思想方法，培养数学核心素养［J］.数学教学通讯，2017（13）：55-56.