四点共圆角关联 截长补短线转换

许婧

摘 要：对一道为“a+b=c型”八年级奥林匹克几何问题，从三种思路入手，进行解法探究.抓住图形结构特征，厘清图形几何性质，是探索已知条件与所求结论之间的逻辑关系的基础，是寻找解决这类几何问题突破口的关键.

关键词：几何性质；解法；变式；反思

1 问题呈现

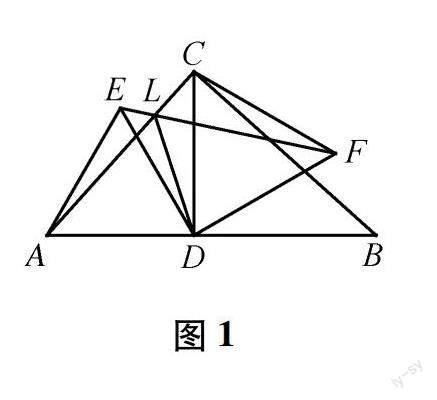
（第18届沙雷金几何奥林匹克通讯赛八年级组第3题）如图1，在直角△ABC中，∠ACB=90°，CD为AB边上的高，作正△AED和正△CFD，其中E，C在AB同侧，F，B在CD同侧，直线EF和AC交于点L.求证：FL=CL+LD.

2 几何性质

抓住图形结构特征，厘清图形几何性质，是建立已知条件与所求结论之间的逻辑关系的基础，也是解决几何问题的基本策略.如图2，根据已知条件，易知△ABC是直角三角形，△AED和△CFD是两个具有公共顶点D的正三角形，

这是图2的基本结构特征，由此易联想到“手拉手”几何模型.从所证结论来看，本题需要证明三条线段之间的和差关系，不妨称之为“a+b=c型”几何问题.

基本性质1 AC=EF.

根据已知，易知AD=DE，DC=DF，∠ADE=∠CDF=60°，所以∠ADC=∠EDF，从而可得△ADC≌△EDF，AC=EF.

基本性质2 ∠ALD=∠ALE=60°.

因为△ADC≌△EDF，所以∠CAD=∠FED，从而易知A，D，L，E四点共圆.根据圆的性质，易知∠ALD=∠AED=60°，∠ALE=∠ADE=60°，所以∠ALD=∠ALE=60°.

根据基本性质2，易得基本性质3.

基本性质3 ∠DLF=∠CLF=60°.

由此易知C，F，D，L四点共圆.

显然，通过A，D，L，E四点共圆，沟通了∠ALD与∠AED、∠ALE与∠ADE之间的数量关系，即∠ALD=∠AED=60°，∠ALE=∠ADE=60°，所以∠ALD=∠ALE=60°.由此也得到了∠DLF=∠CLF=60°.这些性质是解决本题的关键条件，借助60°的角可构造等边三角形，从而能够实现有关线段之间的相互转换，为利用“截长补短法”解决问题创造有利条件.

3 解法探究

思路1：利用“截长法”证明

证法1：如图3，在线段FL上取一点G，使LG=CL.

由基本性质3，得∠CLF=60°.

∴△CLG是等边三角形，

∴CL=CG，∠LCG=∠DCF=60°.

∴∠LCD=∠GCF.

又∵CD=CF，

∴△CLD≌△CGF，

∴LD=GF.

从而可得FL=LG+GF=CL+LD.

证法2：如图4，在线段FL上取一点G，使LG=LD.

由基本性质3，得∠DLF=60°.

∴△DLG是等边三角形，

∴LD=GD，∠LDG=∠CDF=60°.

∴∠CDL=∠FDG.

又∵CD=FD，

∴△CLD≌△FGD，

∴CL=FG.

从而可得FL=LG+FG=LD+CL.

点评：证法1～2都是“截长法”，证法1是在线段FL上截取与线段CL相等的线段，然后证明截剩部分与线段LD相等.证法2是在线段FL上截取与线段LD相等的线段，然后证明截剩部分与线段CL相等.这两种证法的本质都是在较长线段上截取一段等于欲证的两条较短线段中的一条，然后证明截剩部分等于另一条较短线段.对于“a+b=c型”几何问题，都可考虑利用“截长法”解决问题.

思路2：利用“补短法”证明

证法3：如图5，在线段AL上取一点G，使LG=LD.

由基本性质2，得∠ALD=60°.

∴△LDG是等边三角形，

∴DL=DG，∠LDG=∠ADE=60°.

∴∠ADG=∠EDL.

又∵∠ADC=∠EDF=90°，

∴∠CDG=∠FDL.

又∵CD=FD，

∴△CDG≌△FDL，

∴CG=FL.

从而可得FL=CL+LG=CL+LD.

点评：这种证法不唯一，也可以通过△ADG≌△EDL证明AG=EL.根据基本性质1，得AC=EF，从而可得CG=FL.

证法4：如图6，延长DL到點G，使LG=CL，连接CG.

由基本性质2，得∠ALD=60°.

∴∠CLG=60°.

∴△CLG是等边三角形，

∴CL=CG，∠GCL=∠DCF=60°.

∴∠DCG=∠FCL.

又∵CD=CF，

∴△DCG≌△FCL，

∴DG=FL.

从而可得FL=LG+LD=CL+LD.

证法5：如图7，延长LD到点G，使LG=FL，连接FG.

由基本性质2，得∠ALE=60°.

∴△LFG是等边三角形，

∴FG=FL，∠GFL=∠DFC=60°.

∴∠DFG=∠CFL.

又∵DF=CF，

∴△DFG≌△CFL，

∴DG=CL.

从而可得FL=LD+DG=LD+CL.

证法6：如图8，延长LC到点G，使LG=FL，连接FG.

由基本性质2，得∠ALE=60°.

∴∠FLG=60°，

∴△LFG是等边三角形，

∴FG=FL，∠GFL=∠DFC=60°.

∴∠CFG=∠DFL.

又∵FC=FD，

∴△CFG≌△DFL，

∴GC=LD.

从而可得FL=CL+GC=CL+LD.

点评：证法3～6都是“补短法”，这种证法有两种基本思路，一是将较短线段a（或线段b）进行延长，使得延长部分等于另一条较短线段b（或线段a），然后利用全等三角形的性质证明a+b=c；二是将较短线段a（或线段b）进行延长，延长部分的长度为d，使a+d=c，然后利用全等三角形的性质证明b=d即可.对于“a+b=c型”几何问题，都可考虑利用“补短法”解决问题.

思路3：利用特殊图形的性质证明

證法7：（利用角平分线的性质证明）如图9，过点F作FG⊥LD，FH⊥LC，垂足分别为G，H.

由基本性质3，得∠DLF=∠CLF=60°，

∴LF平分∠CLD，

∴FG=FH.又∵FL=FL，

∴△FGL≌△FHL，∴LG=LH.

又∵∠HFL=30°，

∴FL=2LH=LG+LH.

易知△FGD≌△FHC，∴DG=CH.

∴FL=LG+CL+CH=LG+CL+DG=LD+CL.

点评：根据图形的基本结构特征，∠DLF=∠CLF=60°，即LF是∠CLD的平分线，故可考虑利用角平分线的性质解决问题.由此可以看出，角平分线的性质也是证明线段相等的常用方法.

证法8：（利用托勒密定理证明）如图10，由基本性质3，得∠DLF=60°.

又∵∠DCF=60°，

∴∠DLF=∠DCF，

∴L，D，F，C四点共圆.

由托勒密定理，得FL·CD=CL·DF+LD·CF.

又∵CD=DF=CF，

∴FL=CL+LD.

点评：根据图形的基本结构特征，易得到L，D，F，C四点共圆，从而可考虑利用托勒密定理解决问题.这种证法反映了问题的本质特征和命题背景，证明过程非常简洁，是本题的一种最优证法.由此可以看出，托勒密定理是解决与圆内接四边形有关的线段长度问题的基本工具.

4 问题变式

如图11，在直角△ABC中，∠ACB=90°，CD为AB边上的高，作正△AED和正△CFD，其中E，C在AB同侧，F，B在CD同侧，直线EF和AC交于点L，直线EF和BC交于点G.

求证：FG=|LD-CL|.

限于篇幅，证明从略，请读者自行证明.

5 解题反思

5.1 抓住图形结构特征，突破问题解决瓶颈

抓住图形结构特征，厘清图形几何性质，是探索已知条件与所求结论之间的逻辑关系的基础，是寻找解决几何问题突破口的关键.当已知条件与所求结论之间的逻辑关系不明显时，需构造辅助线，使已知条件与所求结论之间的逻辑关系外显化，从而突破问题解决瓶颈.在解决本题的过程中，借助“四点共圆”实现了已知角与未知角的关联，为理清图形几何性质奠定了基础，为“截长补短”实现线段转换找到了突破口.

5.2 夯实“四基”“四能”，培养创新素养

2022版新的《义务教育数学课程标准》提出的初中阶段的数学核心素养有：运算能力、抽象能力、空间观念、几何直观、推理能力、数据观念、模型观念、应用意识、创新意识.上述赛题的解法探究中，“截长补短法”是解决“a+b=c型”几何问题的最基本的思想与方法，是学生应该掌握的基本技能，也是学生在数学学习中积累的数学基本活动经验.只有这样，学生才能从多角度思考问题，创新解决问题思路，从不同视角给出问题的创新解法，从而培养学生的数学核心素养.

参考文献：

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［2］ 赖卓君.四点共圆在几何问题中的应用分析［J］.数理天地（初中版）.2023（11）：4-5.

［3］ 王洪学.“四点共圆”模型［J］.初中生辅导，2023（15）：48-49.

［4］ 周国强，周运柳.解析几何中“四点共圆”问题的转化求解［J］.中学生数学，2023（5）：20-22.

［5］ 闵文彬.辅助线法解几何问题中的“截长补短”思想［J］.数理天地（初中版），2023（5）：26-27.

［6］ 彭阳.截长补短法在初中几何教学中的应用策略［J］.考试与评价，2019（12）：61.

［7］ 陈柳.“截长补短”法应用中所蕴含的“旋转”思想［J］.中学数学研究（华南师范大学版），2017（19）：42-43.

［8］ 单墫.解题研究［M］.上海：上海教育出版社，2016.

［9］ 罗晓棠.追本溯源，拓展思维——对“截长补”法的再探究［J］.初中数学教与学，2020（21）：15-17.

［10］ 李景芝.神奇的“截长补短”——谈截长补短法的应用［J］.中学生数理化（八年级数学）（配合人教社教材），2017（10）：10-11.