以简驭繁,初中数学几何模型教学的探索
李嘉敏
【摘要】几何教学是初中数学教学的重点和难点,在几何教学中逐步归纳出来的几何模型是帮助学生解决几何难题的有效工具.从复杂的图形中抽离出简洁的几何模型,便能直观形象地得到图形性质,从而解决问题.文章中,笔者结合一道广州中考原题,针对其隐含的几何模型进行了分析和梳理,并提出几点反思意见,旨在为广大教育工作者提供教学参考.
【关键词】几何模型教学;数学建模;核心素养
数学教育的目标可分为显性目标与隐性目标两种,显性目标一般指具体的数学知识内容,《义务教育数学课程标准(2022年版)》中的数学学科核心素养属于隐性目标.数学教学除了传授知识外,还要促使学生的理性思维得到良好发展.教师在教学中要引导学生在复杂的几何图形中抓住解题的关键要素,抓住问题的主要特征,忽略次要因素,找出清晰简洁的解题模型,化繁为简、以简驭繁.以下是笔者对一道广州中考原题隐含的几何模型的分析,以及利用该题进行专题复习的教学设计.
一、对“共顶点、等线段”旋转模型的分析
“共顶点、等线段”旋转模型(也称“手拉手模型”)是指已知条件中出现两条线段有公共端点,且它们的长度相等,此时用图形变换的眼光去看,可以理解为其中一条线段绕着它们的公共端点旋转可以得到另一条线段.那么如果把其中的一条线段放在一个封闭图形(如三角形)中考虑,可看作把该线段所在封闭图形绕着线段的公共端点旋转得到另一个与之全等的封闭图形,通过旋转,既可改变线段之间相对的位置关系,也可得到新的图形性质.
二、基于“共顶点、等线段”旋转模型的教学设计
(一)题目呈现

(3)若點M,N分别在线段CA,CB上运动(不含端点),经过探究发现,点D运动到每一个确定的位置,△DMN的周长有最小值t,随着点D的运动,t的值会发生变化,求所有t值中的最大值.
(二)教学分析
1.考题来源
考题的基本图形源于人教版九年级上册教材90页第14题,原题如下:如图2,A,P,B,C是☉O上的四个点,∠APC=∠CPB=60°,判断△ABC的形状,并证明你的结论.
对比分析可知,中考题的第(1)问把教材中题目的题设和结论调换了位置,把已知“角平分线”得出“等边三角形”,改成了已知“等边三角形”求证“角平分线”,考查层次并未明显加深.
2.考点和学情分析
本题考查了圆周角定理、等边三角形性质、圆内接四边形性质、旋转的应用、轴对称的应用、解直角三角形等知识,是一道对数学综合能力要求较高的题目.
初三的学生已经系统完成了初中阶段所有新课学习,掌握了初中平面几何中常用的图形定义、性质和判定知识,也对常见模型有一定了解,但对几何模型的应用还不够灵活,遇到综合题时不能迅速地根据条件联想构建几何模型来解决问题.
(三)教学过程
1.问题展示,揭示课题
课件展示本文“题目呈现”中的题目.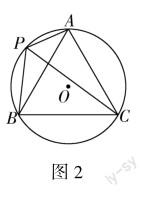
设计意图:让学生关注中考考题动向,并认识到几何模型在解题中的作用.
2.合作探究,解决问题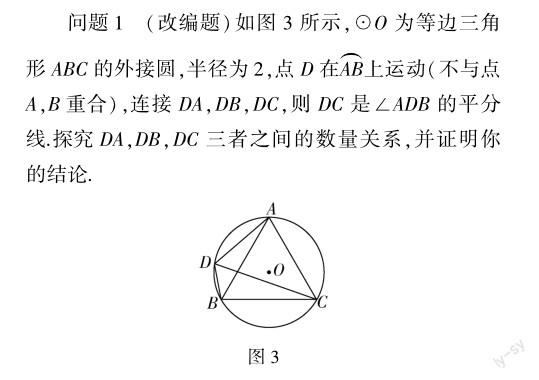
思维流程图(如图4、图5):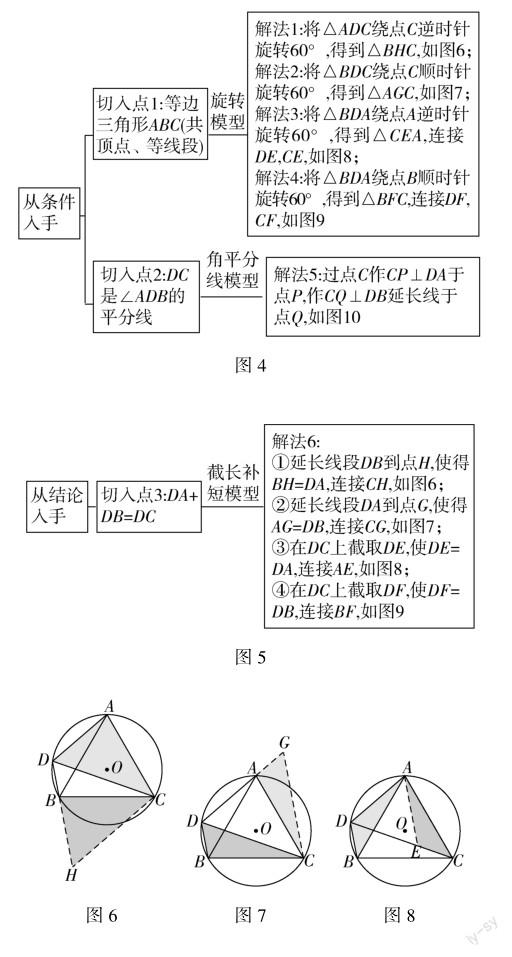
解法分析:从题目条件分析,条件中给出等边三角形ABC,则有等边三角形的三条边相等,所以有“共顶点、等线段”条件出现,例如线段CB和线段CA就有公共端点C,且它们长度相等,可以认为线段CB能由线段CA绕点C逆时针旋转60°得到,这给解题提供了相对明显的提示,通过构造旋转模型来转换目标线段DA与DB的相对位置,从而在新图形中得到更多的几何关系来解决问题.
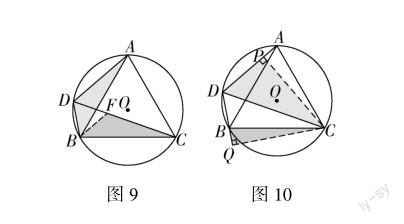
如解法1,将△ADC绕点C逆时针旋转60°,得到△BHC.由圆内接四边形ADBC可得∠DAC与∠DBC互补,再由旋转前后图形全等可得∠HBC与∠DBC互补,证得D,B,H三点共线,进而得出等边三角形DCH,最后通过线段间的等量代换得出结论.解法2~4的解题思路与解法1大致相同,但值得注意的是,解法3和解法4中图形旋转后点D的对应点在线段DC上,需要推理证明.
从另一个角度分析,本题还有一个重要条件是“DC是∠ADB的平分线”,可联想构造角平分线模型来解决.解法5中,易证得△DPC≌△DQC和Rt△APC≌Rt△BQC,DA+DB=DP+DQ=2DP,再通过含30°角的Rt△DPC可得斜边DC=2DP=DA+DB.
本题还可从结论入手分析.题目要求先猜想线段长度关系再求证结论,通过有目的性地测量可以猜想本题目标是求证“DA+DB=DC”,此外显然指向了截长补短模型,解法6的四种构造方法,均是解决线段和差关系的常用方法.
设计意图:启发学生突破解题难点,合理猜想,构造几何模型形成解题思路,通过师生合作探究,让学生学会辨析条件与结论.与此同时,利用问题1为解决中考原题做好铺垫.
3.回归考题,突破难点
问题2 问题1中,四边形ADBC的面积S是线段DC的长x的函数吗?如果是,求出函数解析式;如果不是,请说明理由.
思维流程图(见图11):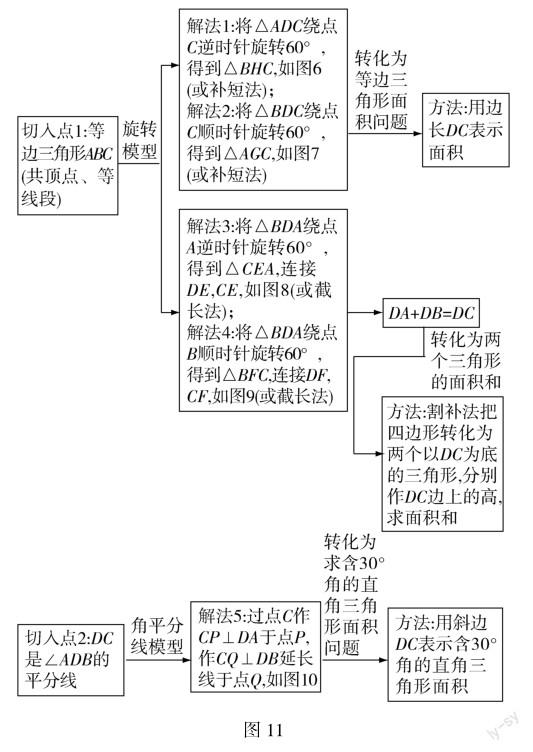

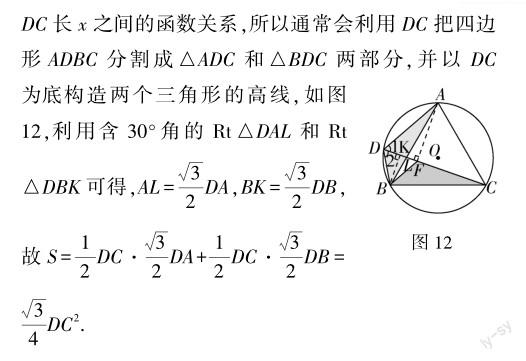
与问题1的分析角度类似,本题也可利用DC是角平分线作为解题切入点,构造角平分线模型(如图10),将四边形ADBC的面积转换成两个全等的含30°角的直角三角形的面积和.
设计意图:在问题1的基础上进一步引发思考,回归中考原题,引导学生从不同角度思考条件和结论,利用一题多解让学生明白题目背后隐藏的深层次问题和结论,培养学生从复杂图形中分离不同几何模型的能力,提升学生逻辑推理、数学建模、直观想象等核心素养.
4.变式应用,突破自我
结合上述问题解析过程中的几何模型,改变题目条件和结论,引导学生对比分析題目异同,帮助学生灵活应用.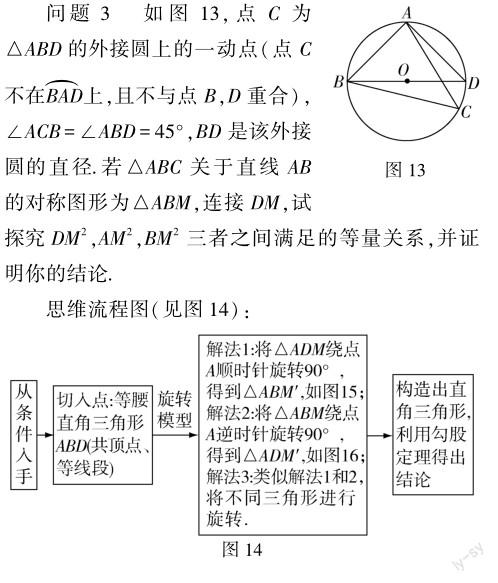
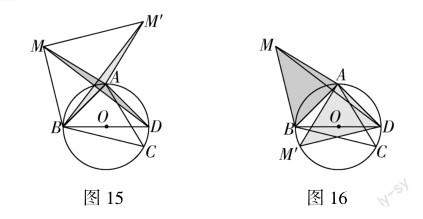
设计意图:紧扣中考热点压轴题,从45°和直径联想到等腰直角三角形,再联想到旋转模型,进行拓展训练,培养学生的审题能力,让其辨析题目中的条件和结论的特点,从而找出对应的几何模型,解决问题.
5.模型总结,能力提高
梳理本节课重点应用的模型以及涉及的模型(见表1):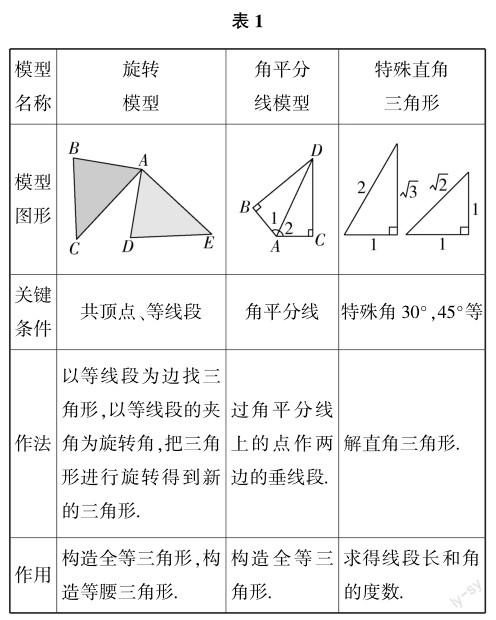
三、初中几何模型教学反思
(一)要注重基本几何图形的积累,运用几何模型化繁为简
图形是最直观的了解知识点之间联系的中介,教师在教学过程中通过画草图、逐步分解,可以强化数学视觉意象之间的关联性.学生掌握几何模型越熟练,他们在解决几何问题时就越容易快速筛选关键信息.对于几何难题,教师在教学过程中可把抽离出的模型单独板书呈现,要注意从复杂图形中抽离出基础几何模型,逐个击破.
(二)要关注几何模型内在数学逻辑,以简驭繁
几何模型可在一定程度上帮助学生便捷地构造出关键图形来解决问题,但教师在教学过程中不能简单地套用模型,必须揭示几何模型中蕴含的图形关系,以及解决数学问题的思维过程.教师可利用几何模型串联起多道难题,实现一“解”多题,统整知识网络,以简驭繁.另外,教师还可以通过变式教学来加强知识之间的渗透和迁移,激发学生的发散性思维,培养学生的思维灵活度.
(三)几何教学要开放探究,培养多角度几何模型思维
在问题情境不变的条件下,几何模型的思维定式能帮助学生应用已掌握的方法迅速解决问题,但在情境发生变化时,这种定式反而会妨碍学生寻找新的方法解决问题.要想消除思维定式的负面影响,教师在教学中就要注重发散学生思维,放大学生的想象空间,利用不同几何模型对题目进行剖析,培养学生多角度的几何模型思维.
(四)提高学生画图、用图的能力
“数形结合”是数学解题中重要的思想之一,图形可以给予人们丰富的信息,对于解题往往可以起到事半功倍的效果.引导学生用图形展示解题思路,能把解题过程中复杂而繁多的条件直观地表示成已知条件和待求解结论,还能加深学生对几何模型的认识,培养学生的直观想象能力.
【参考文献】
[1]原晓萍.视觉思维理论在高中数学教学中的应用研究[D].济南:山东师范大学,2012.
[2]周伟萍.基于APOS理论的初中数学几何模型教学的题组设计———以长方形模型为例[J].中学数学,2021(06):17-18,21.
[3]马小飞.基于几何模型的初中数学教学设计与反思———以一道中考题复习教学为例[J].中学数学研究(华南师范大学版),2020(16):31-34.
[4]徐春凌.分析模型教学对于初中几何数学教学的意义[J].数理化解题研究,2021(02):25-26.
[5]李强.初中几何证明教学要注重“三个关注”[J].数学通报,2021,60(03):29-32.

