基于数学建模思想的贝叶斯公式教学方法研讨

马德宜 柳福祥 崔盛

【摘要】《概率论与数理统计》是几乎所有大学生都需要学的一门课程，贝叶斯公式是《概率论与数理统计》中的重要公式之一.文章由贝叶斯公式的实际应用题出发，首先，基于贝叶斯理论给出解答过程；其次，基于数学建模的思想，对题目进行拓展，分析贝叶斯公式与次品率之间的关系，得到该次品来自甲车间生产的可能性随着甲车间的次品率的增大而增大的结论，分析贝叶斯公式与占有率之间的关系，得到当甲车间的产品占全厂的比例在区间[0.2，0. 5]时该次品来自丙车间生产的可能性最小的结论；最后，通过源码和图形仿真验证结论.

【关键词】贝叶斯公式；数学建模；仿真验证

【基金项目】高等学校大学数学教学研究与发展中心2021年教学改革项目（CMC20210504）

国内外已有许多学者从不同角度对与贝叶斯公式相关的教学进行了研究，比如在线课程设计、课程思政、数学建模、后验分布、统计推断等.虽然贝叶斯的相关知识在教材上有许多例题，但是大部分都是以贝叶斯公式为基础进行求解的.文章将以贝叶斯公式为基础，对应用问题进行拓展，考虑各种极值情况，最后再用Matlab进行仿真，并以图形可视化形式展现最后结果，让贝叶斯公式更加通俗易懂.

一、贝叶斯公式

由此可见，该产品由甲车间生产的可能性最大.

三、贝叶斯公式与次品率之间的关系

对于上述例1，基于数学建模的思想进一步讨论下面这个问题.在其他条件不变的情况下，甲车间的次品率下降到多少时该次品来自甲车间生产的可能性不是最大？

以0.001为步长，将甲车间的次品率从0逐步递增到0.5，绘制该次品来自甲、乙和丙车间生产的可能性与甲车间次品率之间的关系.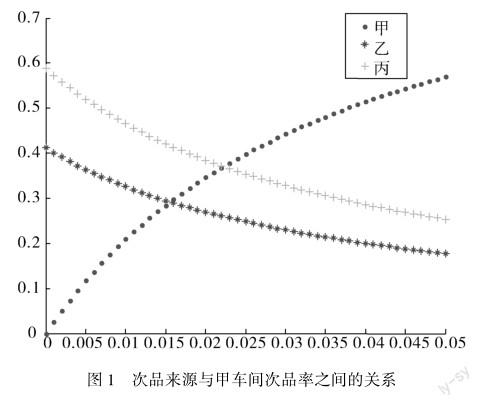

数学建模仿真结果和数学公式分析结果相一致，从两种不同角度分析贝叶斯公式，让学生更加清晰地认识贝叶斯公式.

四、贝叶斯公式与占有率之间的关系

（一）丙占有率为20%

对于例1，基于数学建模的思想进一步讨论下面这个问题.在其他条件不变的情况下，甲车间的产量占全厂多少时该次品来自甲车间生产的可能性不是最大？

以0.01为步长，固定丙车间的产量占比为20%，将甲车间的产量占比从0.05逐步递增到0.75，绘制该次品来自甲、乙和丙车间生产的可能性与甲车间产品占比之间的关系.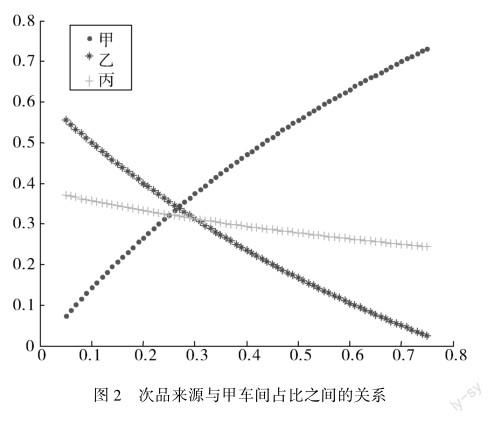

可以发现，当甲车间的产品占全厂的比例大于0.267时该次品来自甲车间生产的可能性最大；当甲车间的产品占全厂的比例小于0.267时该次品来自乙车间生产的可能性最大；当甲车间的产品占全厂的比例在[0.25，0.30]之间时该次品来自丙车间生产的可能性最小.

数学建模仿真结果和数学公式分析结果相一致.数学建模给出了直观图形，数学公式给出了理论推理，让学生从多角度思考贝叶斯公式.

（二）丙占有率为40%

对于例1，基于数学建模的思想进一步讨论下面这个问题.在其他条件不变的情况下，甲车间的产量占全厂多少时该次品来自甲车间生产的可能性不是最大？

以0.01为步长，固定丙车间的产量占比为40%，将甲车间的产量占比从0.05逐步递增到0.55，绘制该次品来自甲、乙和丙车间生产的可能性与甲车间产品占比之间的关系.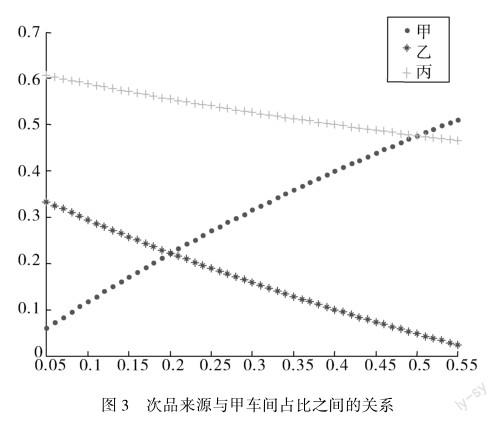

可以发现，当甲车间的产品占全厂的比例大于0.5时该次品来自甲车间生产的可能性最大；当甲车间的产品占全厂的比例小于0.2时该次品来自甲车间生产的可能性最小；当甲车间的产品占全厂的比例在[0.2，0.5]之间时该次品来自乙车间生产的可能性最小.

五、小 结

基于贝叶斯求解的应用题有许多，比如：

例2 已知5%的男人和0.25%的女人是色盲，现随机地挑选一人，此人恰为色盲，问此人是男人的概率（假设男人和女人各占人数的一半）？

例3 按以往概率论考试结果分析，努力学习的学生有90%的可能考试及格，不努力学习的学生有90%的可能考试不及格.据调查，学生中有80%的人是努力学习的，问考试及格的学生是不努力学习的人的概率？

这种类似例题，都可以仿照本文方法进行拓展，然后进行仿真，让学生更加生动形象地理解贝叶斯公式的含义.

【参考文献】

[1]韩云娜，张静.概率论与数理统计在线课程教学设计与创新：以“全概率公式与贝叶斯公式”为例[J].电脑知识与技术，2021（13）：115-116，140.

[2]李广玉，田研.“課程思政”理念指导下的贝叶斯公式教学[J].惠州学院学报，2020（06）：126-128.

[3]曹建美，冯晨娇，王凤翔.将数学建模思想引入“贝叶斯公式”教学中的案例实施[J].江苏科技信息，2020（34）：57-59.

[4]程伟丽，李晓霞.后验分布在贝叶斯统计课堂教学的延伸[J].高等数学研究，2018（01）：74-78.

[5]胡顺奇，公维丽.贝叶斯统计推断的经典教学实例解析[J].中国统计，2018（10）：41-43.