数学建模过程中的模型优化算法

楚晓媛

【摘要】随着我国社会主义现代化建设的不断发展，我国的科学技术水平实现了前所未有的提升，其对数学思维的应用也更加广泛，对于解决实际问题有着重要的意义与价值.本文将引入历届数学建模竞赛优秀的论文，着重对数学建模过程中的模型优化算法进行深入探讨，通过对模型优化算法策略的研究，为解决实际问题提供一个参考与借鉴.

【关键词】数学建模；模型优化；算法；转化模型

改革开放以来，我国对教育给予了高度的重视.数学建模作为高等院校数学专业极为重要的组成部分，其不仅能够促进数学与现实世界的联系，而且能够在一定程度上提升学生的逻辑思维能力与解决实际问题的能力，然而在数学建模过程中也普遍存在着优化模型求解的难题，因此，对数学建模过程中模型优化计算的探究有着重要的实用价值与研究意义.

一、数学建模相关概述

所谓数学建模，就是通过一系列的科学计算得出相应的结果，进而用来解决现实生活中的实际问题，并能够接受相关检验而建立起来的数学模型.当对某一个特定问题或实际问题进行分析的过程中，人们需要对与该问题相关的各项信息进行有效的调查，并在掌握基本信息的基础上，做出科学假设，对其内在规律进行有效分析，并能够通过数学符号语言进行相应的描述，进而建立完整的数学模型.改革开放以来，我国的计算机信息技术取得了前所未有的发展，数学建模在工程技术、自然科学等行业得到了充分的应用，且正朝着经济、金融、环境等各个领域渗透，已经成为现代社会一种新型的高新技术产品，在社会生产与生活中发挥着不可替代的作用.数学模型的建立需要对现实问题进行深入剖析，并强调对数学知识的灵活运用，其与计算机技术共同成为知识经济时代的重要工具.

二、数学建模过程中的模型优化算法

（一）对特殊关系式的巧妙处理

通过以往的数学建模可以发现，部分数学优化模型不能够直接通过软件技术进行结果输出，这很大程度上是由于模型目标函数中含有特殊的关系式，如不等式等，这些关系式无法采用软件直接求解，基于这一现象，可以充分利用0-1变量，并通过合成技术对这类问题进行计算.如原油的采购与加工类问题：

其模型目标函数出现了多个分段函数：

c（x）=10x，0≤x≤500，1000+80x，500≤x≤1000，3000+6x，1000≤x≤1500.

对于该模型，可以直接对其各个分段函数做出相应的处理，可以将x三个区间设由（0-1变量）进行控制，其函数值可以通过对三个区间的有效整合，对函数值进行合成，可以对函数图像进行探究，并结合函数值，引入变量yk和非负变量zk.基于特殊关系式模型，需要对以下问题进行深度分析：（1）有甲必不能有乙的排斥关系；（2）在m约束中共有k个有实际作用；（3）建模中含有绝对值的式子.

（二）降低可行域

在进行数学优化模型构建时，需要加强身体，能够充分利用题目中给出的各项信息，做出大胆的猜想与假设，也可以通过直接信息元素得出相关信息，增加约束条件，这不仅能够在一定程度上降低模型求解的难度系数，而且能够对问题的求解起到决定性作用.以某年生产车辆的安排为例，要想能够降低运输成本，必须保障使总运量以及出动卡车的数量达到最低，需要满足铲点与卸点在平均时间内完成目标，便可以称之为无冲突，并以此建立相关的数学模型.在这个过程中很容易将约束条件局限于电铲能力、产量任务等方面.因此，可引入变量0-1，并通过fi描述确定i号铲点的使用情况，实现对电铲数量的有效约束∑10i-1fi≤7，fi∈{0，1}，除此之外，还可以适当增加对卡车数的相关约束：xij≤AijBij，分别采用xij，Aij，Bij代表铲点i到卸点j的发车次数、同行运行卡车数以及最多可运行次数等，然后通过卸点运行一周期所用的平均时间可以得出相应的结果.

（三）对模型的有效转化

通常，对于一些计算起来比较困难的数学模型，可以通过转化的方法，使模型的难度得到大大降低，然后再进行相应的求解计算，常用的转化方法有离散问题连续化、连续问题离散化等，以易拉罐下料问题为例，其决策变量采用的是整数形式，再加上生产数量的巨大，可以将其看作实数，进而转化为线性规划.再如飞行管理相关问题，可以进行非线性规划，通过已知条件：飞机速度等同，可以将这一距离约束问题转化成角度约束问题，便于计算.这些例子都在一定程度上体现了数学建模中模型转化的优越性.

（四）优化计算方法的灵活选用

1.三大非经典算法

在数学建模过程中，通常会遇到对非线性关系复杂数据进行拟合的参数，在这种条件下，可充分引入人工神经网络，这种方法不仅无需对相关函数关系进行假定，而且能够对复杂的非线性函数进行有效的模拟，能够对题目中的各

项数据进行充分有效的利用.另外，对于优化组合类问题，则可以采用遗传算法与模拟退火算法，如某年的钢管订购与运输问题，采用的是非线性规划模型，传统的算法很难顺利实现求解，而采用遗传算法则能够实现很快求得最优结果.

2.蒙特卡罗算法

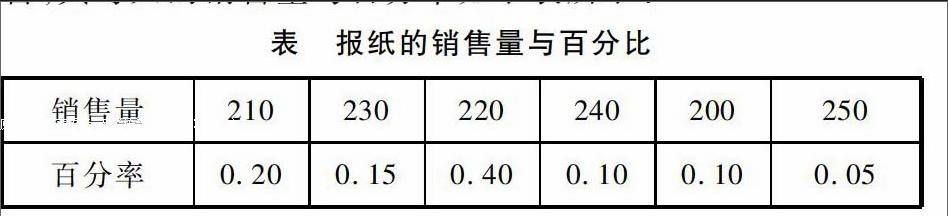
数学建模中难免会遇到随机规划模型问题，对于此类问题可采用蒙特卡罗计算方法，例如：每份报纸价格为0.02元，某报童以该价格买进报纸，并以0.05元/份的价格出售，其每天的销售量与百分率如下表所示：

从题面上可以得知未销售的报纸以0.02元/份退还报社，所求的是报童每天买进多少份报纸才能保证其平均收益达到最大.对于这一问题，可采用模拟方法，做出相对合理的预测，然后通过数学建模对猜想进行验证，另外还可以对随机优化模型进行求解，这些都能够应用到实际生活中，实现对现实问题的有效解决.

3.支持向量机算法

支持向量机算法能够有效弥补神经网络在局部极值问题方面的缺陷，其在预测以及综合评价领域应用较为广泛，如1989年数学建模大赛中蠓的分类问题，已知两种不同类型蠓虫的触角长度与翅膀长度，要求对15只蠓虫进行分类鉴别，采用支持向量机的计算方法，通过二次规划模型的建立，可以求得一个分类函数，然后将相关数据带入便可求得结果，该计算方法快捷、有效.

结束语

近年来，社会各个行业对数学建模的应用日趋广泛，数学建模与优化方法的联系更加密切，在社会生产与生活中得到了前所未有的应用，在数学建模中，都不同程度地包含了最优计算思想，而这些最优理论又是通过具体的数学建模形成的，因此，必须加强对数学建模的重视，准确把握当前数学建模过程中存在的各项问题，实施科学的优化计算策略，提升其在社会实际问题中的作用与价值.

【参考文献】

[1]董文瑾.大学数学教学过程中数学建模意识与方法的培养[J].大科技，2014，24（2）：28-29.

[2]李冬梅，陈东彦，宋显华.基于创新人才培养的数学建模考核方法探析[J].黑龙江教育：高教研究与评估版，2014，15（7）：52-53.

[3]李晓玲，杨慧贤.浅谈独立学院数学建模教学的探索与研究[J].价值工程，2014，24（15）：259-260.

[4]张建忠.关于高职院校数学课程开展数学建模实践教学的思考[J].机械职业教育，2015，10（12）：142-144.

[5]BenTal A，Shamailov S S，Paton J F R.Central regulation of heart rate and the appearance of respiratory sinus arrhythmia：New insights from mathematical modeling[J].Mathematical Biosciences，2014，255（3）：71-82.