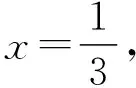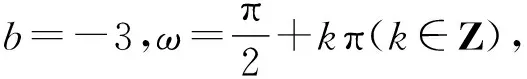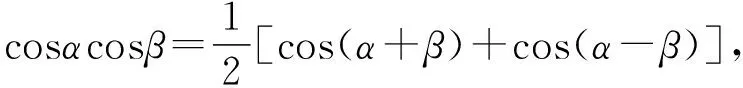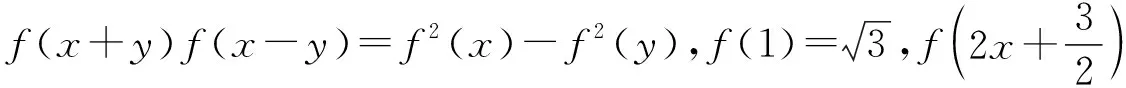函数性质扑朔迷离 三角模型拨云见日
——谈构造三角函数模型解决抽象函数问题
唐 洵
(福建省福清第三中学)
新高考以来,以抽象函数性质为背景的问题屡见不鲜,此类问题大体上有两种解法:一种是通过变换函数性质的表达式配合赋值法得到相应的结论,此方法虽为通法,但过程较为复杂,有时令人难以琢磨;另一种是根据题设的性质条件或所给表达式的结构特征构造相应的三角函数模型进行求解.那么如何选择合适的三角函数模型?当题目中有多个函数时应当如何选择?在构造的过程中有什么注意点?下面笔者结合此类问题的几种题型进行讲解.
1.预备知识,磨刀不误砍柴工
1.1 奇偶性结论
(1)若f(ωx+φ)为奇函数,则f(x)的图象关于点(φ,0)中心对称.
(2)若f(ωx+φ)为偶函数,则f(x)的图象关于直线x=φ对称.
1.2 对称性结论
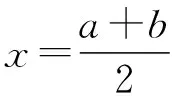

1.3 周期性结论
(1)若f(x+a)=f(x+b),a≠b,则f(x)为周期函数,且T=|b-a|;若f(x+a)+f(x+b)=c,a≠b,则f(x)为周期函数,且T=2|b-a|.
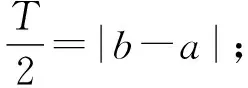
1.4 导函数结论
(1)若函数f(x)可导且图象关于直线x=a对称,则其导函数图象关于点(a,0)中心对称;若函数f(x)可导且图象关于点(a,0)中心对称,则其导函数图象关于直线x=a对称.特别地,若偶函数可导,则其导函数是奇函数;若奇函数可导,则其导函数是偶函数.
(2)若某函数的导函数为奇函数,则该函数为偶函数;若某函数的导函数为偶函数,则该函数不一定是奇函数,但其图象一定有对称中心.
(3)若周期函数可导,则其导函数仍是周期函数(周期不变),反之不成立.
1.5 三角函数和、差与积的关系式
(1)积化和差:
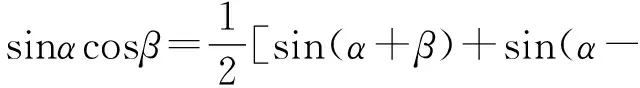
(2)和差化积:
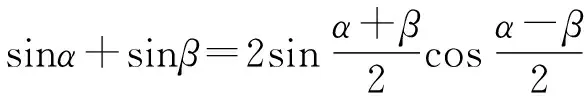
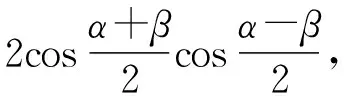
2.题型剖析,吾将上下而求索
2.1 基于单函数性质的构造
【例1】(2021·全国新高考Ⅱ卷·8)已知函数f(x)的定义域为R,f(x+2)为偶函数,f(2x+1)为奇函数,则( )
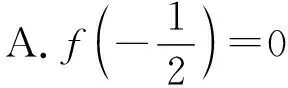
C.f(2)=0 D.f(4)=0
【答案】B
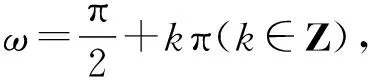
【点睛】若题设条件给出的是f(ax+b)的奇偶性(对称性)、周期性、特殊值等相关性质时,可以此为契机,将f(ax+b)构造成满足题设条件的三角函数;若选择将f(x)构造成三角函数,则需先将f(ax+b)的性质还原为f(x)的性质后再构造,相对复杂,非必要时不采用.
【例2】(多选)(2023厦门二模)定义在R上的函数f(x)满足f(2-x)=f(2+x)+4x,函数f(2x+1)的图象关于点(0,2)对称,则( )
A.f(x)的图象关于点(1,2)对称
B.4为f(x)的一个周期
C.f(2)=4
D.f(2 023)=-4 042
【答案】AD
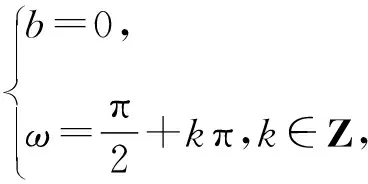
【点睛】为了增加题目的难度,命题者有时会刻意隐藏函数的奇偶性或对称性的信息,仅通过给出某个表达式让该性质若隐若现,如本题中给出“f(2-x)=f(2+x)+4x”,此时需要通过认真观察、正确书写、充分挖掘、适度联想,找出奇偶性或对称性后,构造合适的三角函数模型.
2.2 基于单函数及其导函数性质的构造


C.f(-1)=f(4) D.g(-1)=g(2)
【答案】BC
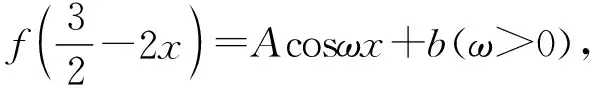

【例4】(多选)(2023池州二模)已知函数f(x)及其导函数f′(x)的定义域均为R,且f(x)在R上单调递增,记g(x)=f′(x),若f(3x-2)+f(4-3x)=f(3),g(x)+g(4-x)=4,则( )
A.f(-1)=0
B.f(f(1))>f(0)
C.g(f(-1)) 【答案】ABD 【点睛】构造三角函数模型研究抽象函数,目的是将抽象的性质形象化,但在多选题中,对于一些简单的选项,可以通过直接赋值或者简单的代数变换得到,如本题中的A,B选项,并且本题在构造出g(x)后,由于还原为原函数的未知量较多,还需借助f(-1)=0进行辅助,因此有时需要双管齐下进行解题. 2.3 基于双函数性质的构造 【例5】(多选)(2023安徽模拟)已知函数f(x),g(x)的定义域均为R,f(x+1)-1是奇函数,g(x+2)是偶函数,f(x)-g(x+2)=4,g(2)=3,则( ) A.f(x)为奇函数 B.4为f(x)的一个周期 C.f(2 023)=-1 【答案】BD 【点睛】双抽象函数的问题特征是两个函数时而分离,时而聚集,如本题中“f(x+1)-1是奇函数,g(x+2)是偶函数,g(2)=3”体现了两个函数各自的性质,而“f(x)-g(2+x)=4”体现了两个函数之间的联系,因此只要能够确定一个函数的模型,另外一个自然迎刃而解.由于本题中g(x+2)同时出现在“分离”与“聚集”中,因此对g(x+2)进行构造. A.-21 B.-22 C.-23 D.-24 【答案】D 【点睛】由于题设给出的函数性质均涉及g(x),因此本题选择g(x)构造三角函数.值得注意的是,在构造的过程中,可以先由g(x)图象的对称性得到g(x+2)为偶函数,再利用待定系数法确定相应的数据,最后通过f(x)+g(2-x)=5得出f(x). 2.4 基于双函数及其导函数性质的构造 【例7】(多选)(2023枣庄一模)已知函数f(x)和g(x)及其导函数f′(x)与g′(x)的定义域均为R,若f(x+2)-g(1-x)=2,f′(x)=g′(1+x),且g(x+1)为奇函数,则( ) A.函数y=g(x)的图象关于直线x=2对称 C.函数y=g′(x)的图象关于点(2,0)对称 【答案】ACD 【点睛】在求解本题时,也可以根据g′(x+1)是偶函数,构造g′(x+1)=Acosωx+b(ω>0)进行求解,要注意导函数为偶函数,原函数未必为奇函数;此外,此构造在还原为原函数时所带系数相对复杂一些,但也能正确解题. 【例8】(多选)(2023湖北八市3月联考)设定义在R上的函数f(x)与g(x)的导函数分别为f′(x) 和g′(x),若g(x)=f(2x-1)-2x,且f(x) 与g(x+1)均为偶函数,则下列说法一定正确的是( ) A.f′(1)=1 B.f′(2 023)=2 023 【答案】ABD 【点睛】本题若直接根据f(x)与g(x+1)均为偶函数或者f′(x)与g′(x+1)均为奇函数进行构造,容易陷入构造误区,无法使得题设条件同时成立;此时应当对题设条件先分析,再构造;另外本题的函数并非单纯的三角型函数,在构造时应当结合题设数据作出分析. 2.5 基于联想公式的构造 A.-3 B.-2 C.0 D.1 【答案】A 【点睛】本题解题的难点在于需要通过题设表达式的结构特征,联想出对应的三角函数公式,进而得到相关的三角函数后,再利用待定系数法进行求解;考虑到问题为求值,还可以使用赋值法进行求解,具体如下:令x=1,y=0,得f(0)=2,令x=1,y=1,得f(2)=-1,令x=2,y=1,得f(3)=-2,令x=3,y=1,得f(4)=-1,令x=4,y=1,得f(5)=1,令x=5,y=1,得f(6)=2=f(0);令x=6,y=1,得f(7)=1=f(1),以此得到一个周期的值,进而得到答案. 则( ) A.f(0)=0 B.f(x)为偶函数 C.f(3+x)=-f(3-x) 【答案】ACD 3.归纳小结,为有源头活水来 【问题1】构造三角函数模型求解问题的题目特征是什么? 【答案】当题设条件呈现函数的奇偶性、对称性、周期性等性质,或是给出一个类似于三角函数公式的表达式时,考虑构造三角函数求解,常见的设问为求值或者研究函数的对称性与周期性. 【问题2】如何合理地构造三角函数模型? 【答案】若题设给出的是函数的相关性质,则需在分析性质的基础上进行构造,最好能够基于一个奇函数或者偶函数进行构造;若题设给出的是某个三角函数的公式,需要结合公式中的三角函数进行构造. 【问题3】在确定大致的三角函数模型后,仍然有很多未知的参数,此时应当如何进一步得到更加精确的三角函数? 【答案】在确定大致的三角函数模型后,需进一步根据题设中的条件,利用待定系数法得到其他的系数,但并不能保证所有的系数都能被求出. 【问题4】当题设中既有原函数又有导函数的性质时,应当如何作出选择? 【答案】当二者同时出现时,应优先选择原函数构造三角函数模型,此时要注意将导函数的性质还原成原函数性质时的一些易错点,如导函数为偶函数时,原函数不一定是奇函数. 【问题5】当题设和问题比较简单时,应当如何作出选择? 【答案】直接利用函数的性质进行变换处理或者直接构造简单的三角函数进行求解即可.