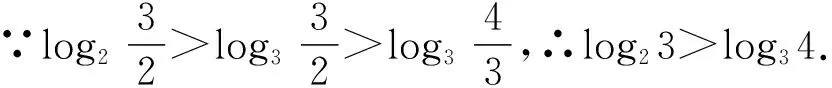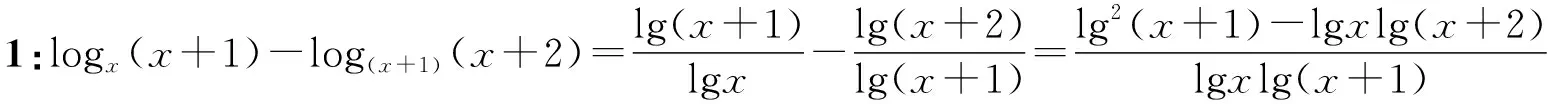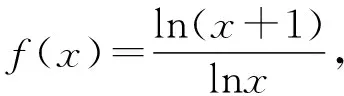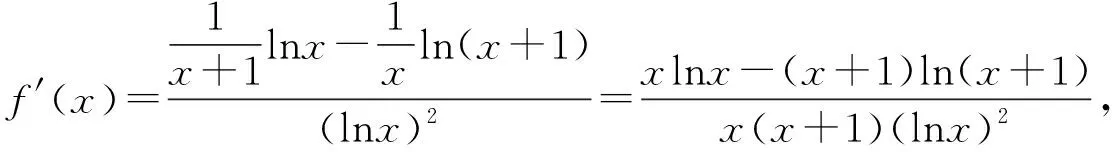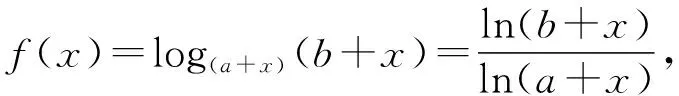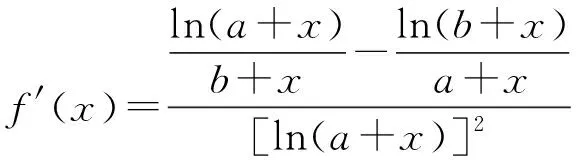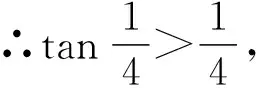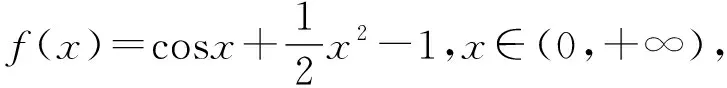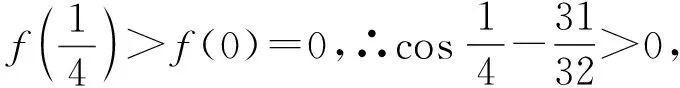一题多解 教材生根 锤炼素养——以教材中的一道比较对数值大小习题为例

邓成兵

(四川省成都市航天中学校)

通过对2017年到2022年全国高考试题分析,不难发现,这六年均出现“比较对数值大小”的试题,而且难度在逐年由借助0和1来比较向压轴题转化(如统计表所示).

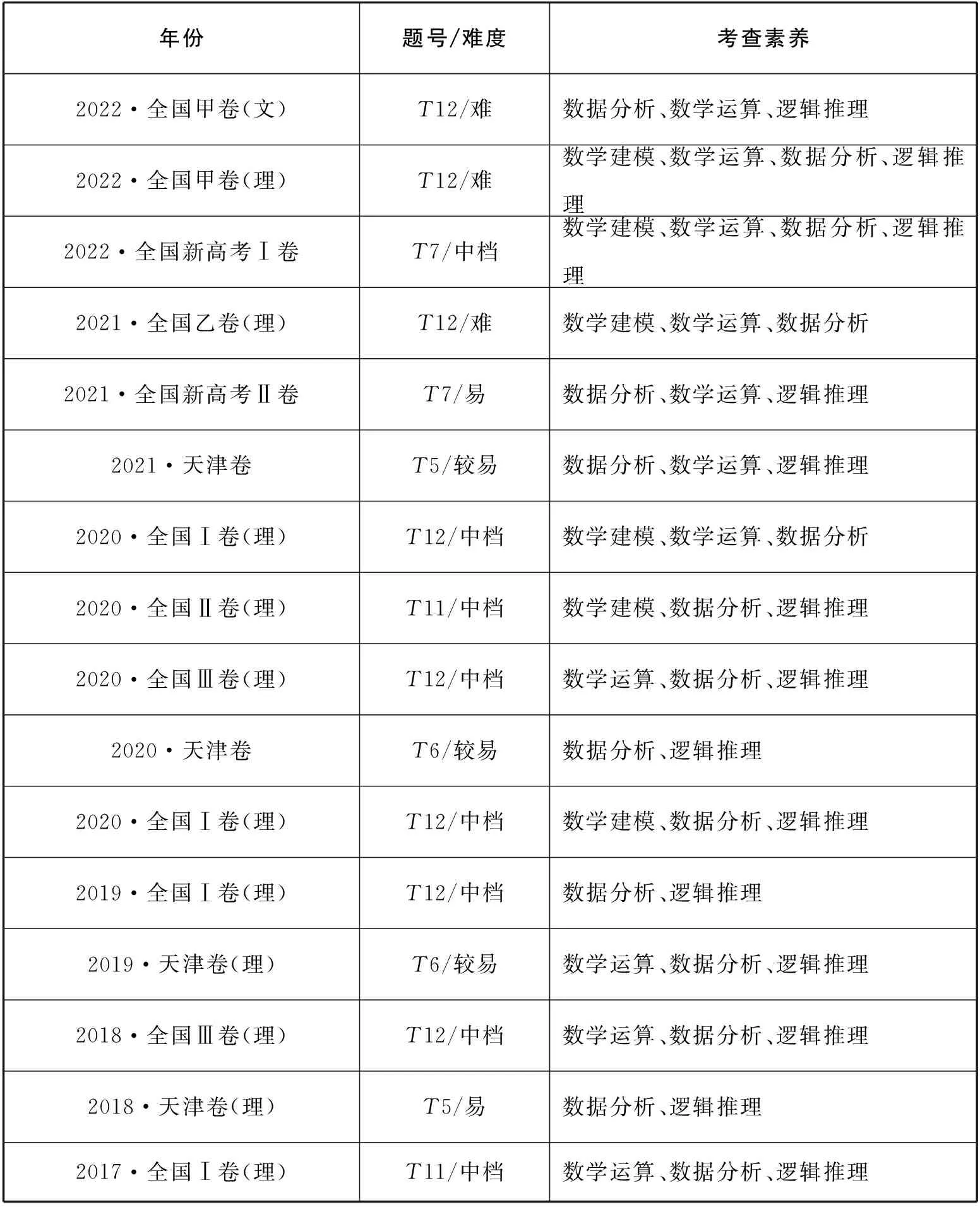
2017—2022年全国高考真题对数比较大小双向细目表

教材是高考试题的“策源地”.很多试题的产生都来自教材的例习题的组合、加工和深化,所以大部分师生都能感受到数学高考试题是年年岁岁花相似,岁岁年年题不同,每年试题都给人一种“似曾相识”的感觉.

1.例题探究

每年高考试题都重在考查学生的基本知识、基本思想和基本技能.对学生的思维量、灵活性、数学核心素养均提出较高要求.高考试题源于课本的原型题或改编题,其所占比例非常高,这就要求教师要排除题海战术的干扰,精心筛选课本的例习题,引导学生吃透教材的例习题,并进行一题多解、一题多变.本文以2019年人教A版《数学必修第一册》第141页第13题(2)问为例,与大家交流.

1.1教材溯源,完善认知

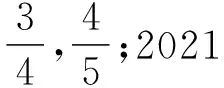
1.2解法探究,锤炼素养

生1:这还不简单吗?直接利用对数换底公式和我们常用的lg2和lg3的值代入比较.

其中lg2=0.301,lg3=0.477,可知log23≈1.58,log34≈1.26,log45≈1.16,

∴log23>log34>log45.

师:不错!这样做虽然简单,但如果记不住lg2和lg3的值或换成其他对数值,我们该如何进行比较呢?

生2:老师,我知道,直接作差,再利用换底公式和基本不等式进行比较.

∴(ln3)2-ln2×ln4>0,即log23>log34.

同理可得log34>log45.综上所述,log23>log34>log45.

生3:既然可以利用作差+基本不等式作比较,那么利用作商法也可以进行比较.

∴log23>log34,比较log34>log45可以用生2的方法.

生4:老师,在生2和生3同学的提醒下,我想到可以用作差+换底公式进行比较.

∴log23>log34,比较log34>log45可以用生2的方法.

点评:生2、生3和生4采用的比较法(作差或作商),先将对数化为同底,由于对数没有乘法或除法,但可以相加,不约而同地利用基本不等式进行适当的放缩,最终可以比较大小.

生5:既然可以利用比较法+基本不等式作比较,那么我们也可以利用糖水不等式进行比较.

即log32log34.

同理可得log34>log45.综上所述log23>log34>log45.

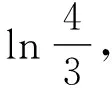
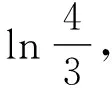
点评:解决这类问题的关键是在对数换底公式基础上,设法利用教材例题的结论将问题转化为分母相同的两个分数的大小关系问题.

生6:老师,我也想到利用对数的运算性质进行比较.

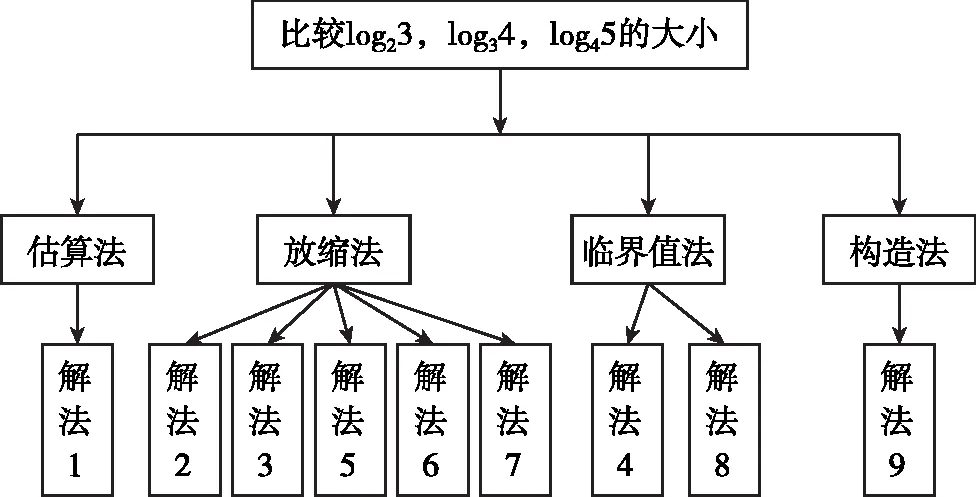
log23=log2333=log827,log34=log3242=log916

由对数函数的图象可得,在第一象限,对数函数的图象底大图低,

∴log827>log927⟹log23>log34.

同理可得log34>log45.综上所述log23>log34>log45.

点评:以上判断的三个对数值都是在(1,2)中,比较的关键是小数部分的大小比较,所以引入对数的运算,把log23与log34的比较转化为log2333与log3242的比较,再利用单调性进行比较.只不过缺乏中间值选取的策略指导,所以初步的估值是明确突破问题难点的关键.

师:比较对数中的底数和真数不同,一般是利用中间量法0和1,能否把三个对数值范围转化在(0,1)之间,再进行比较呢?

生7:能.解法如下:

同理可得log34>log45,∴log23>log34>log45.

点评:把三个对数值转化到(0,1)范围内,再结合对数函数的单调性比较.

师:如果直接求这三个对数值的中间量,我们该如何找?依据又是什么呢?

生8:哦,老师,我知道了.由于log23,log34,log45都在(1,2)之间,可以利用二分法来确定中间量.

4log34=log344=log3256>5=5log33=log335=log3243,

4log45=log454=log4625<5=5log44=log445=log41024.

综上所述log23>log34>log45.

点评:既不同底又不同指的指数式、对数式比较大小,不能直接利用函数的单调性来比较,一般可以取一个介于两值中间且与题目中两数都能比较大小的一个中间值,进而利用中间值解决问题,把这种方法叫作临界值法.利用临界值法比较大小,关键点是寻找中间变量,该如何寻找呢?本解法分为两个步骤:

(1)估算要比较大小的两个值所在的大致区间;

(2)可以对区间使用二分法(或利用指对转化)寻找合适的中间值.

师:除了上述方法外,请同学们观察每个对数的底数和真数有什么关系?能否用一个函数来表示?

(同学们齐声说:可以用f(x)=logx(x+1),且x>1表示)

师:如果能证明出函数f(x)=logx(x+1)的单调性,问题就迎刃而解.

生9:可以同生2同学的解法一样,利用作差+基本不等式进行证明,证明如下:

∴logx(x+1)>log(x+1)(x+2),

∴函数f(x)=logx(x+1)在(1,+∞)上单调递减,∴log23>log34>log45.

师:除了同生9同学用作差法+基本不等式证明外,还有其他方法吗?

生10:老师,可以用导数法证明,证明如下:

易证xlnx<(x+1)ln(x+1)在(1,+∞)上成立,∴f′(x)<0在(1,+∞)上恒成立.

故函数f(x)在(1,+∞)上单调递减,∴log23>log34>log45.

师:通过生9和生10的证明,得到函数f(x)=logx(x+1)(x>1)是单调递减函数.

把此结论推广到更一般的通用结论:当10,则logab>log(a+x)(b+x).

∵10,

∴(a+x)ln(a+x)<(b+x)ln(b+x),则f′(x)<0,

∴函数f(x)在(1,+∞)上单调递减,得证logab>log(a+x)(b+x)成立.

点评:观察式子结构构建函数模型,根据数字出现频率,设定自变量x适用条件,这种方法叫作构造函数.大多时候,三个数比较大小,可能某一个数会被刻意的隐藏了“同构”规律,所以可以优先从结构最近的两个数去分析,再利用逆用函数的单调性,构造函数.本题利用同构获得一般性结论:当10,则logab>log(a+x)(b+x),当10,则logba>log(b+x)(a+x),从而多途径引导学生巧妙构建数学模型.

1.3思维导图,锤炼素养

在新高考大背景下,为了让数学的解题思路更清晰有序,且能够高效精准的将高中数学题目中所给定条件的知识点与自己大脑系统中已有条件的相关知识体系建立一个恰当有效的有机联系,笔者认为可以借助思维导图来完成,复杂的知识点经过思维导图呈现,理解起来就清晰多了.如本题的思维导图如下所示(生1、生2……分别对应解法1、解法2):

2.链接高考,迁移经验

本题的解法主要有四大类,一是估算法;二是放缩法;三是临界值法;四是构造法,这些方法当然也能迁移到对应的高考试题中,如下试题.

(1)(2018·全国Ⅲ卷(理)·12)设a=log0.20.3,b=log20.3,则( )

A.a+b

B.ab

C.a+b<0

D.ab<0

则a+b≈0.748-1.738=-0.990,ab≈0.748×(-1.738)≈-1.300,

∴ab

解法2:∵0

∴ab<0,a+b<0.

点评:此真题用到了方法一估算法和方法二放缩法.

(2)(2022·全国甲卷(文)·12)已知9m=10,a=10m-11,b=8m-9,则( )

A.a>0>bB.a>b>0

C.b>a>0 D.b>0>a

∴a=10m-11>10lg11-11=0.

∴b=8m-9<8log89-9=0.综上,a>0>b,故选A.

点评:此真题解法采用了作商+基本不等式求解.

(3)(2020·全国Ⅲ卷(理)·12)已知55<84,134<85.设a=log53,b=log85,c=log138,则( )

A.a

C.b

【解析】由题意可知a,b,c∈(0,1),无法用临界值0和1比较.

∵4log53=log534=log581,3=3log55=log553=log5125,

∵4log85=log854=log8625,3=3log88=log883=log8512,

点评:此解法考查临界值法.

A.c>b>aB.b>a>c

C.a>b>cD.a>c>b

则f′(x)=-sinx+x>0,∴f(x)在(0,+∞)上单调递增,

∴b>a,∴c>b>a,故选A.

点评:此真题解法采用构造函数法和放缩法.

从以上四个高考题的解析分析可以看出,高考题强调通性通法的考查,这些解法立足于教材的典型例习题中.尤其是在高三复习中,教师应该回归教材,注重通解通法,用好用活经典型,巧妙引导学生一题多解、一题多变寻找共性,从而逐渐培养学生的数学核心素养.

3.一题多变,揭示本质

著名数学家波利亚说过这样一句话:“掌握数学也就意味着要善于解题”,所以解一道经典的数学题不能只就题论题或一题多解而草草结束,而是要揭开此题的内涵和价值.为实现这一目的,需要对它进行变式.通过一题多变,不但可以启示我们要注意探索多种题型转变的一般规律,揭示其本质特征;而且还能锤炼学生的核心素养,帮助学生更有效地学习数学.本题进行如下变式,读者可以尝试从通解通法入手,完成下列四个变式题.

【变式1】已知a=log32,b=log43,c=log54,则下列关系正确的是( )

A.a>b>cB.c>b>a

C.b>a>cD.a>c>b

【变式2】已知a=log36,b=log510,c=log714,则下列关系式正确的是( )

A.a>b>cB.c>b>a

C.b>a>cD.a>c>b

【变式3】已知a=log64,b=log96,c=log129,则下列关系式正确的是( )

A.a>b>cB.c>b>a

C.b>a>cD.a>c>b

【变式4】已知a=log0.10.2,b=log0.20.3,c=log0.30.4,则下列关系正确的是( )

A.a>b>cB.c>b>a

C.b>a>cD.a>c>b

【答案】(1)B (2)A (3)B (4)B

点评:作为教师,对于高考中的热点问题,需要做个有心人,将相关题目进行整理归纳,分析其命题的角度和解题的方向,剖析其中的基本思想,让学生在面对此类问题时心中有解题的大方向和清晰的解题策略.

4.教学反思

以上分析可见,一道看似简单的选择题,被挖掘出的价值不亚于一道大题,真是“小小比较,大大学问”.因此要对课本上的一些典型例题进行认真地探究,尤其是在高三复习中一定合理地再利用,挖掘其内在的潜能,综合提高学生解决似曾相识问题的能力,锤炼学生的核心素养.