2023年四省联考第16题的若干思考

黄 雨 顾 飞

(安徽淮南第二中学)

通过对2023年四省联考第16题的分析,确立对逻辑推理问题的有效解法.本次四省联考体现了新高考的大方向,突出数学学科在新高考中的选拔功能.

一、真题再现

【例题】如图为一个开关阵列,每个开关只有“开”和“关”两种状态,按其中一个开关1次,将导致自身和所有相邻的开关改变状态.例如,按(2,2)将导致(1,2),(2,1),(2,2),(2,3),(3,2)改变状态.如果要求只改变(1,1)的状态,则需按开关的最少次数为________.

(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)

【解析】笔者查阅了网上的各种解法,大多比较拖沓冗长,难以理解,更有人说是大学的布尔代数理论,但笔者认为,并没有这么高深.下面笔者采用图表法,轻松搞定.

有两个关键点要明确:

(1)每个开关最多按一次,因为按偶数次和不按是一样的,按奇数次和按一次是一样的,要想按开关次数最少,则开关最多按一次.把开关按一次记为灰色(如图1中,(1,1),(1,2)),不按不变色.

(2)如果一个开关自身和相邻的开关灰色的个数为奇数个,则开关改变(如图1中,(2,1),(2,2),(1,3)),如果为偶数个,则开关不改变(如图1,(1,1),(1,2)).

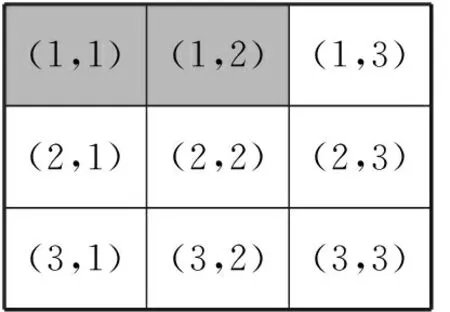
图1

明确了上面两个关键点,下面开始分析:

1.首先分析(1,1)要不要按,与它相邻的(含自身)有三个开关,分别是(1,1),(1,2),(2,1),根据对称性,要么只按(1,1),要么三个都按,按其他的两个对(1,1)没有影响.

2.如果三个都按,如图2(1),显然(1,1),(1,3),(3,1)改变,其他都不变,要想(1,3)不变,只有按(2,3),如图2(2).此时(2,2)变了,若要其不变,只有按(3,2),如图2(3),此时(2,3),(3,2)改变,行不通.

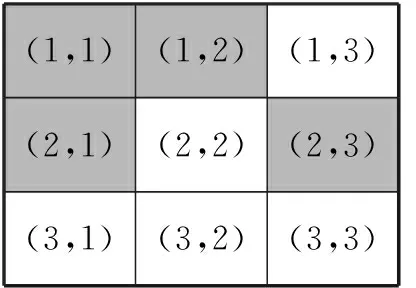
图2(2)

图2(3)

3.如果只按(1,1),如图3(1),显然(1,1),(1,2),(2,1)都变了,若要(1,2)不变,则按(1,3),如图3(2),此时(1,3),(2,3)变了.若要(1,3),(2,3)不变,则需按(2,3),同理,若要(2,1)不变,根据对称性需要按(3,1),(3,2),如图3(3),满足条件.故最少5次.

图3(1)

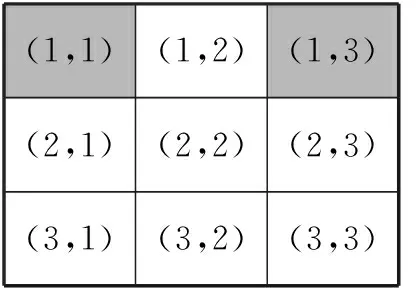
图3(2)

图3(3)

二、题后思考

(1)这题考查了什么?

(2)学生如何才能把问题等价转换成上述两个关键点?

(3)既然是四省适应性考试,这题具有怎样的方向性?

若要回答上述问题,我们还是来仔细阅读《中国高考评价体系》.《中国高考评价体系》明确了“一核”“四层”“四翼”的概念及其内涵,回答了“为什么考”,“考什么”,“怎么考”的问题.

1.从“四翼”来看

“四翼”为考查要求,即“基础性、综合性、应用性、创新性”,回答了“怎么考”的问题.高考关注与创新密切相关的能力和素养,考查学生探索新方法、积极主动解决问题的能力,鼓励学生摆脱思维定式的束缚,勇于大胆创新.

本题以真实情境为背景,通过考查对开关变化规律的分析,探索题目中所隐藏的规律性,大胆创新解决问题的方法,符合高考对创新性的考查.

2.从“四层”来看

“四层”为考查内容,即“核心价值、学科素养、关键能力、必备知识”,回答了“考什么”的问题.必备知识的积累是形成关键能力和学科素养的基础,关键能力是以必备知识的学习探究为载体培养出来的.

本题考查了命题与逻辑推理等必备知识,以及数学学科的多项关键能力.第一、信息识别与获取的能力,根据问题情境的需要对开关阵列进行加工处理,分析其变化内容.第二、数学抽象与概括能力,对开关变化产生的规律进行总结,等价转化成图形特征.第三、逻辑推理与论证能力,通过对(1,1)开关的讨论,分析出最优的设计方案.

3.从“一核”来看

“一核”为考查目的,即“立德树人、服务选才、引导教学”,回答了“为什么考”的问题.本题为四省适应性训练,参照新高考的要求,加入复杂情境,突出数学思维方法,强调育人价值,故对我们今后的教学和学习指出了方向——全面落实立德树人要求,深化数学学科育人价值.

三、延伸应用

【例题】某学校举办数学竞赛,A,B,C,D,E五位同学得到了前五名.发奖前,老师让他们自己猜一猜各人的名次排列情况.

A说:B第三名,C第五名;

B说:E第四名,D第五名;

C说:A第一名,E第四名;

D说:C第一名,B第二名;

E说:A第三名,D第四名.

老师说,每个名次都有人猜对,问这五位同学的名次如何?

【解析】因为关系很多,比较散乱,我们还是通过列表的方式解决,把相关信息列成图表如图4(1).

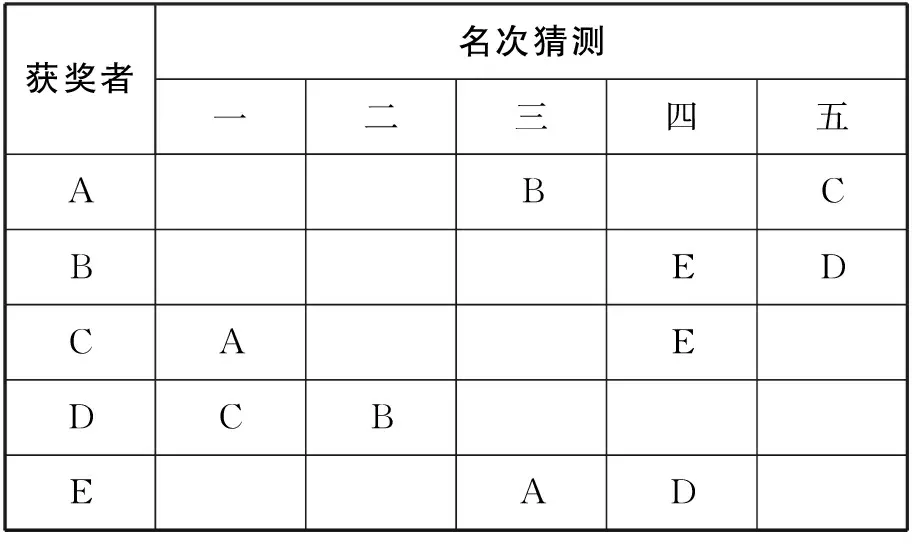
图4(1)

首先明确:正确的涂灰色,错误不涂色,如图4(2).

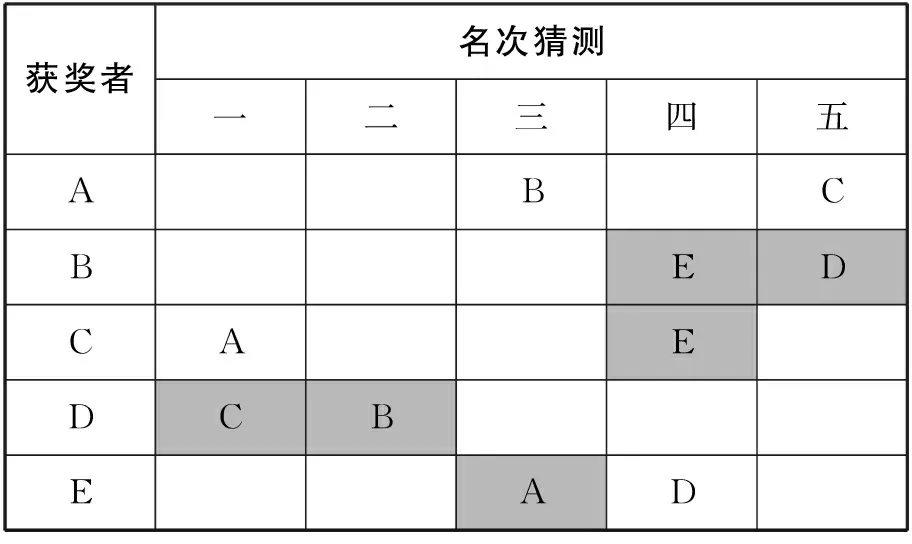
图4(2)

由题意,每个名次都有人猜对,所以由表可知,第四名为E⟹第五名为D⟹第一名为C⟹第三名为A⟹第二名为B.

【点评】将获取的信息进行加工,通过等价转化,将信息表格化,这样能直观地分析出相互之间的逻辑关系.

【变式】一次考试共考了语文、英语、数学、物理和化学五科,每科满分5分(等级分),其余等级依次为4,3,2,1.已知某5个学生按总分由多到少的名次排列是A,B,C,D,E,且满足下列条件:

①在同一科目中及总分中没有得到同样分数的人;

②A的总分是24分;

③C有四门得到相同分数;

④E的物理得5分,语文得3分;

⑤D的化学得4分.

试求出题中未直接给出的每人的其他各科成绩.

【解析】根据题意把信息列成表格,如图5(1),根据图表信息进行填充.

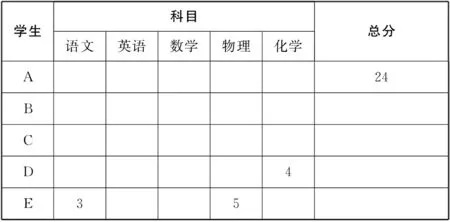
图5(1)

A总分为24分,满分是25分,所以只有一门是4分,只能是物理,如图5(2)灰色部分.

C有四门分数相同,且总分在第三名位置,只能是3分,且为后四门,如图5(2)灰色部分.

B的总分在第二的位置,故前三门为4分,如图5(2)灰色部分.

图5(2)

根据总分的排序,D的英语、数学只能是2分,E的外语、数学只能是1分,如图5(3)灰色部分.

图5(3)

E的化学只能是1分,如果是2分,D最大只能和E相同,矛盾,故E的化学只能是1分,那么D的语文、物理都是2分,剩下的直接填涂,如图5(4)灰色部分.

图5(4)

【点评】当信息量很大时,通常使用图表的方法,能够直观的把关键性信息呈现出来,通过对图表内信息的筛选来确定逻辑推理的方向.从本质上讲即是:收集信息→提炼信息→等价转化→合理推断→得到结果.

本次四省适应性考试指出了高考的大方向,通过设置复杂情境问题,考查数学思维方法,突出数学学科在新高考中的选拔功能.常规的刷题和模型化的学习已经不再适应新高考的要求,要深入理解数学知识本质,经历知识发生发展的过程,这样才能避免因为复杂情境问题而产生的困境.

本文系2021年度安徽省教育科学研究项目“基于数学实验课程建设下的高中生数学学习品质的培养与评价研究”的研究成果,项目编号为JK21099.