一道离心率高考题的解法与变式研究

李 璇

(广东省中山市实验中学)

离心率是圆锥曲线的一个重要性质,也是高考考查的热点问题之一.解析几何的相关题目难度大且计算繁琐,学生对此类题目都比较害怕,难以下手,而离心率问题涉及的知识面广、切入的角度多样,灵活多变,也常常让学生头疼不已,本文通过不同的命题角度对一道离心率高考题进行改编,并对解法进行研究,挖掘离心率问题的解题视角和解题思路,总结离心率问题的解题方法,试图通过该题及其变式,发散思维,使学生学会离心率的相关解题方法,在碰到离心率问题时能做到有法可依.

一、高考真题再现

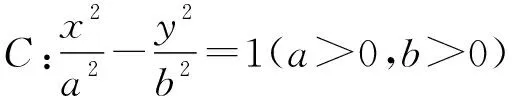
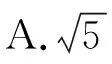
解法一(利用余弦定理的推论)

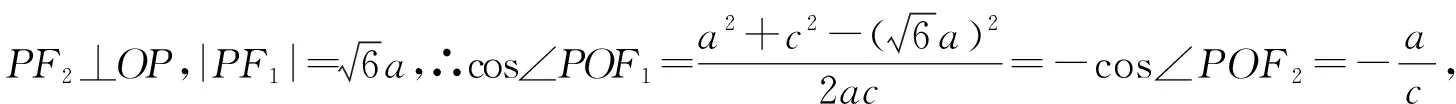
解法二(利用对称与勾股定理)

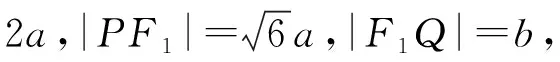
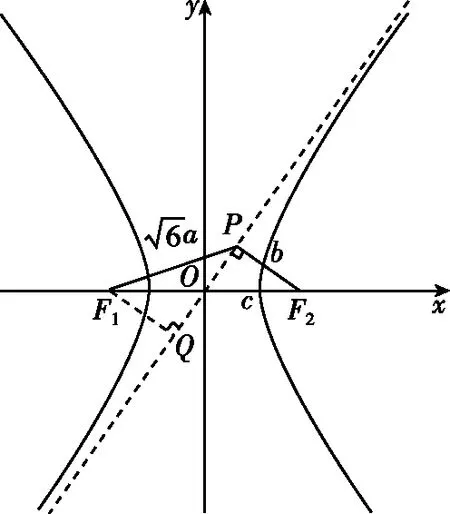
解法三(利用点坐标与两点间距离公式)

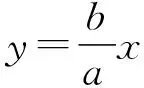
二、高考真题改编

接下来,本文将以该题为载体,将其中的部分条件改变,从不同角度进行命题,并探究离心率问题的不同解题方法.

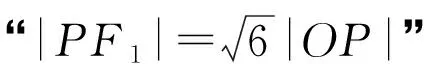
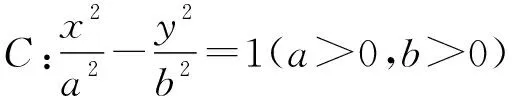
解法一(利用定义与余弦定理的推论)

|MF2|=3|PF2|=3b,由双曲线的定义得|MF1|=3b-2a.

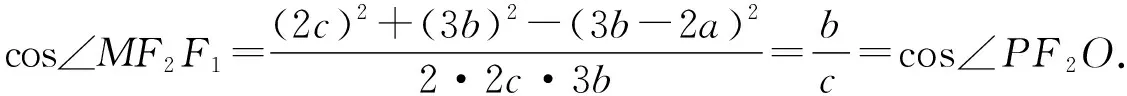
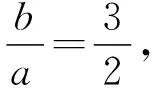
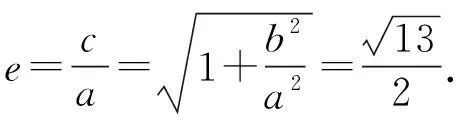
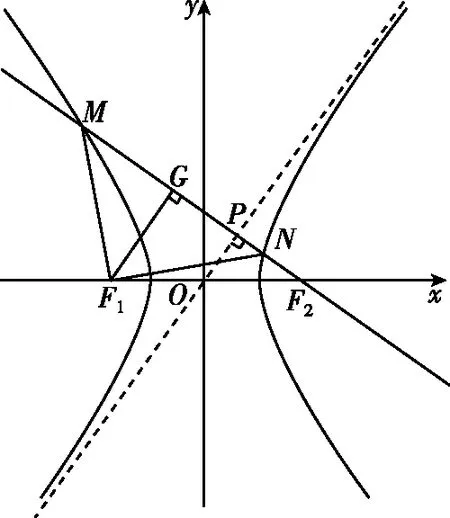
解法二(利用中位线与勾股定理)

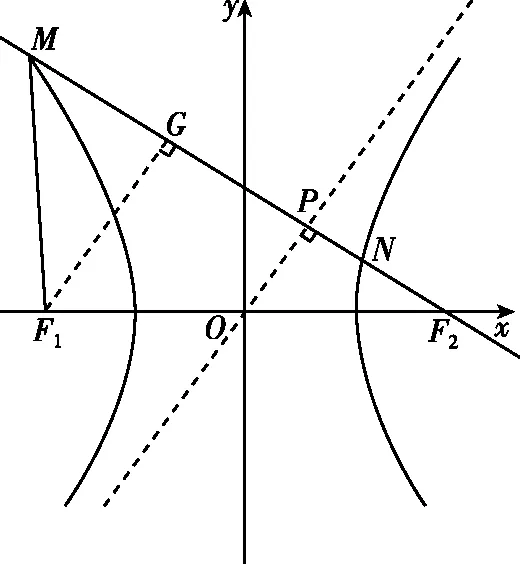
过点F1作F1G⊥MF2于点G,∴OP∥F1G.

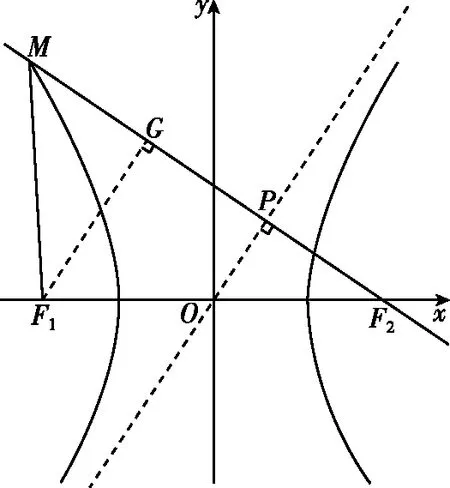
∵OP=a,又O为F1F2中点,

∴|F1G|=2a,|GF2|=2b,∴|MG|=b.

又|MF1|=3b-2a,

∴在Rt△MF1G中,b2+4a2=(3b-2a)2,

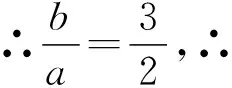
解法三(利用求点坐标与代入点坐标)

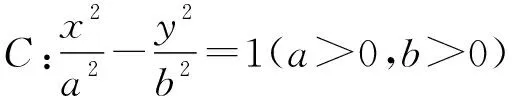
解法一(方法与变式1的解法三相同)

解法二(利用求点坐标与相似比)

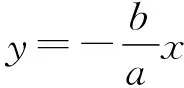
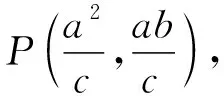
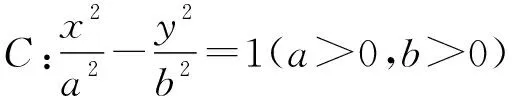
解析(利用定义与两次余弦定理)

设|NF2|=t,则|MF2|=3t,由定义可得,

|NF1|=t+2a,|MF1|=3t-2a.

∴在△MF1F2中,(3t-2a)2=(3t)2+(2c)2-2·3t·2ccos∠MF2F1,

在△NF1F2中,(t+2a)2=t2+(2c)2-2·t·2ccos∠MF2F1.

∴-12at+4a2=4c2-12bt, ①

4at+4a2=4c2-4bt, ②

②-①得,16at=8bt,即2a=b,

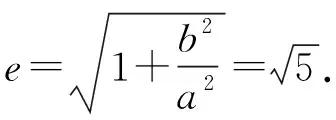
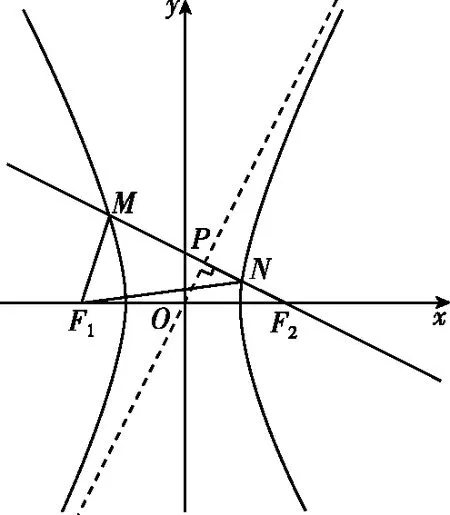
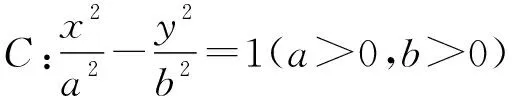
解析(利用定义与几何关系)

过点F1作F1G⊥MF2于点G,则G为MN的中点.

∵|OP|=a,OP是△F1GF2的中位线,

∴|F1G|=2a,|GF2|=2b,

设|MF1|=|NF1|=t,

由定义可得|NF2|=t-2a,|MF2|=t+2a,

|MN|=|MF2|-|NF2|=4a,

则|MG|=|NG|=2a,

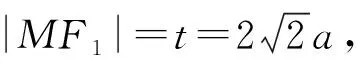
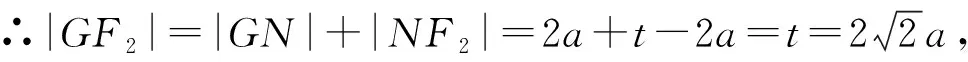
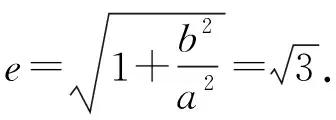
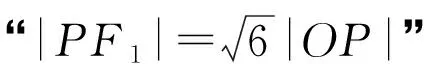
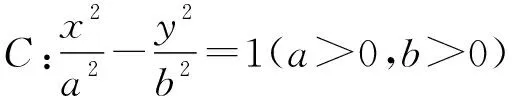
解法一(利用正弦定理与三角函数)

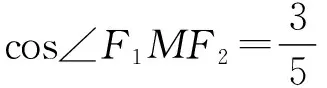
又Rt△OPF2中,

∴在△MF1F2中,

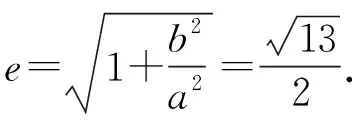
解法二(利用直角三角形中的三角函数与双曲线定义)

过点F1作F1G⊥MF2于点G,则|F1G|=2a,|GF2|=2b,

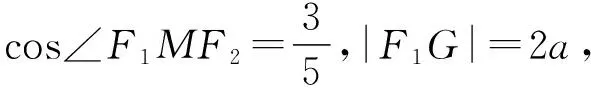
则由定义

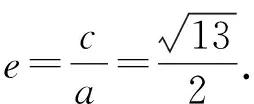
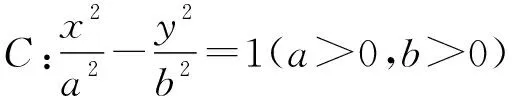
解法一(同变式2方法)

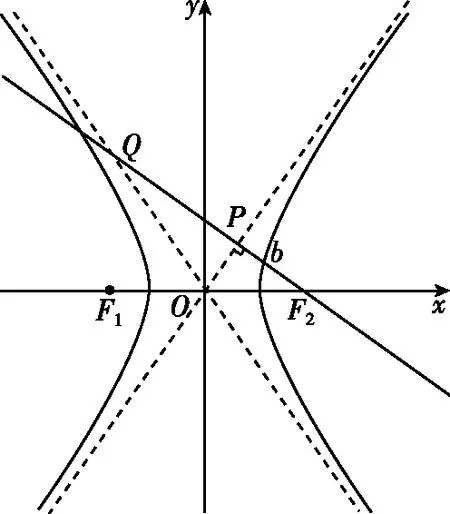
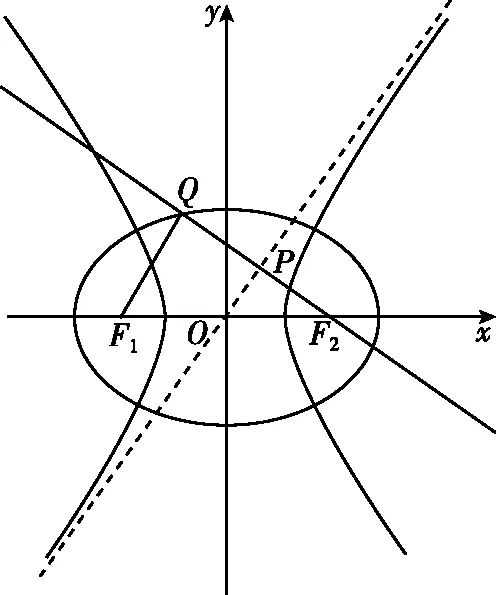
由已知,F1Q∥OP,又O为F1F2的中点,

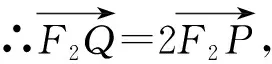
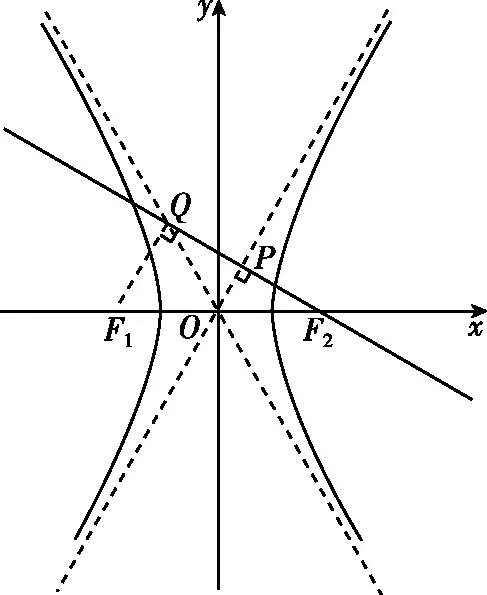
解法二(利用对称与几何性质)

由于两渐近线关于y轴对称,

∴∠POF2=∠QOF1,

由∠F1QF2为直角,O为F1F2的中点,得|OQ|=|OF2|.又P为F2Q的中点,

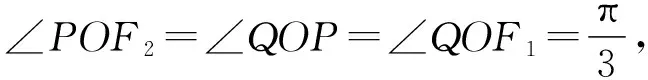
解法三(利用圆与等面积法)

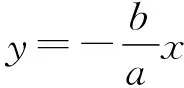
联立两方程可得Q(-a,b),

解法四(利用圆与两点间距离公式)

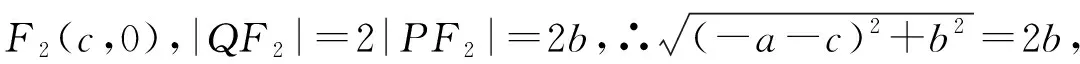
整理得2a2+ac-c2=0,e2-e-2=0(e>1),

解得e=2.

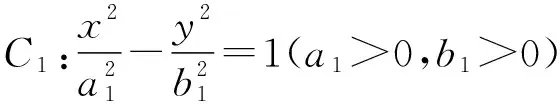
解法一(利用定义与基本不等式)

|QF1|=2a1,|QF2|=2b1,

由椭圆定义,得2a1+2b1=2a2,∴b1=a2-a1,

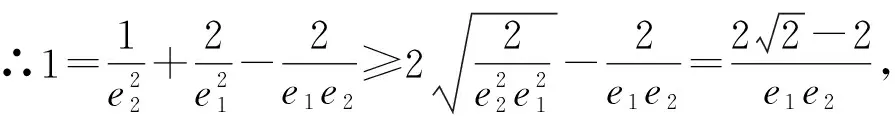
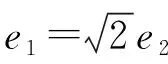
解法二(利用正弦定理与三角函数)

设∠QF2F1=θ,

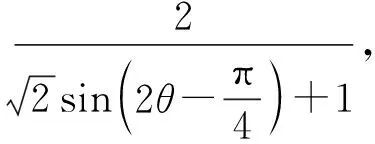
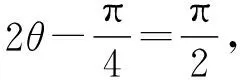
三、方法总结

求解离心率是解析几何中一个重要的问题,是几何与代数相结合的一类题型,它综合性强,涉及面广、知识融合巧妙、切入角度多样,解题时有时一种方法一种策略就可以解决问题,有时则需多种方法策略融合使用.不同的解题视角、不同的解题思路,往往能得到不同的解题效果和体验.

四、教学启示

一题多变、一题多解可以避开题海战术、打破学生思维定式,达到举一反三、提高教学效率的效果.本文以高考真题为载体,进行多个变式,对试题进行有效拓展,并对不同解法进行探究,可开拓学生求异思维,教会学生在不同中找相同,相同中找不同,让学生在不同的问题情境中分析问题的本质,寻找解决问题的切入口.因此,在平时的教学中,应正确运用变式教学,以点带面,通过对题目进行改编变式,拓展学生思维的深度和广度,加深学生对知识的理解,提高学生对知识的灵活应用,培养学生自主探究的能力.