2023年新高考数学命题的智慧点与启示

余继光

(浙江省柯桥中学)

通过对2023年新高考数学命题卷的亮点、特点、考点分布等进行分析比较,挖掘新高考数学命题的新动向,新智慧点,共性与启示,为2024年新高考数学复习展示重点与方向,提升新高考数学复习的有效性.

2023年7份高考数学试卷中,新课标Ⅰ,Ⅱ卷(以下简称新Ⅰ,新Ⅱ),北京,上海,天津5份为新高考卷,前2份由教育部考试中心命制,后3份由三个直辖市单独命制,全国31个省市自治区中,19个参加2023年新高考数学卷的评价,检测新高考改革地区的数学教育教学实际情况.2024年全国将有2/3以上的省市参加新高考数学命题评价.本文重点关注新Ⅰ,新Ⅱ(经典命题,具有高考指挥棒功能),并兼顾其他试卷的智慧点与教学启示.

一、2023年新高考数学卷亮点与特点

1.新高考数学卷亮点

1.1科学评价新题型增多

2017年制定2020年修订的《普通高中数学课程标准》为新高考数学命题制定了评价标准,为实施这一标准,教育部考试中心已将五大新题型渗透到新高考数学命题中,这是高考数学命题的总趋势,因为新题型在评价学生数学核心素养中扮演着十分重要的角色,多项选择题从多个角度综合地审视数学的某一个复杂情境,如新Ⅱ第12题信道传输方案问题;举例题使考生数学思维更加开放,如新Ⅰ第11题;开放题提供更多的选择性,如新Ⅱ第15题;数据分析题体现现实情境中数据信息的重要性,如新Ⅱ第19题疾病诊断数据分析题,上海第14,19题;逻辑推理题正是数学复杂情境的本质特征,特别是自定义题,如上海第16题等.

1.2阅读运算逻辑推理多

新高考数学命题的阅读量明显增加,超过100字数的题目增多,如数学文化题,概率统计题等;由于现实情境与科学情境题目加入,运算量增加,过去高考数学题关注圆锥曲线中的数式运算即可,现在增加了数学文化、概率统计等的代数运算,如新Ⅰ第10题(源于必修第一册,P141,第10题),21题(源于选择性必修第3册,P91,第10题),新Ⅱ第12,19题,上海第19题等.

1.3初等与高等链接增多

导数,极限,级数(不等式,数列背景)等知识点是初等化的象征,新Ⅰ第11,22题;新Ⅱ第22题,天津第19,20题,上海第10题等,都可以与高等数学相关知识关联,此类评价可以发现较强数学思维层次考生.

2.新高考数学卷特点

2.1主干知识点处能力立意

新高考数学试卷中函数(包括三角、数列、导数)、几何(空间几何、平面解析几何)、概率与统计等主干知识模块以其所需要的关键能力为立意之本,从设问角度到问题隐藏的复杂结构都需要应试者通过自身所具有的数学核心素养与关键能力才能突破,比如数学建模能力,新Ⅱ第12,19题,上海第11题等.

2.2多学科交汇处创新链接

以复杂情境为特征,综合化背景覆盖,在数学内在知识交汇点处链接其他学科形成综合,或在不同学科知识交汇处链接形成综合,如新Ⅰ第10题,新Ⅱ第12,19题.

2.3现实科学情境挖掘到位

不论是现实情境还是科学情境,新颖、别致、巧妙设问,使仅靠刷题才能解题的考生望而生畏,如新Ⅰ第10,12,13,21题,新Ⅱ第12,19题,上海第9,11,14,19题等.

3.考点分布、重点模块及分值占比

3.1考点分布

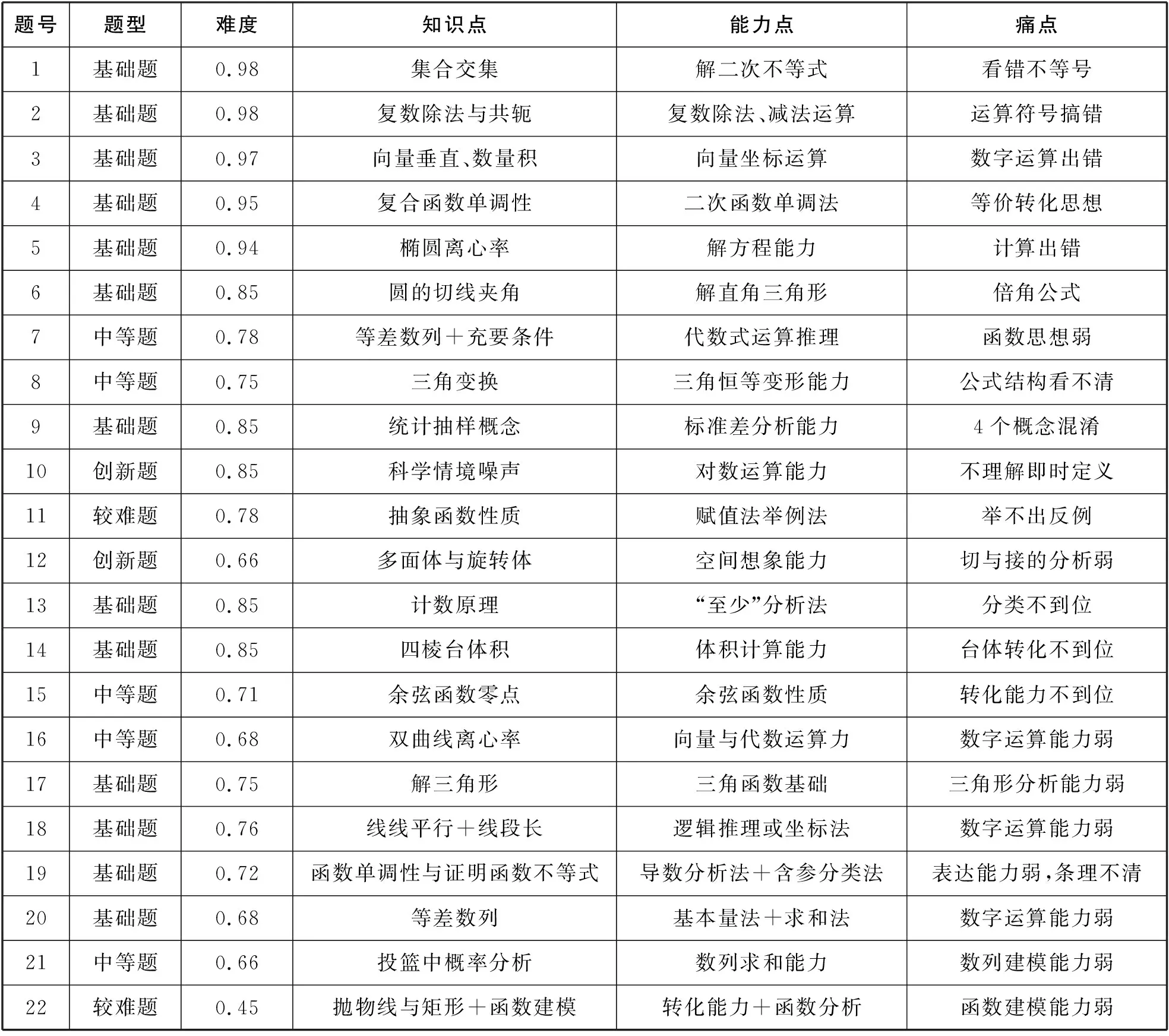
表1 2023年新课标Ⅰ卷中的知识点、能力点与痛点

表2 2022年全国新高考Ⅰ卷中的知识点、能力点与痛点

对照上述两张统计表可以发现:

(1)2023年比2022年基础题增多,样本难度有所下降,特别是开始的单选题,使考生由易到难求解思维顺畅,避免考试心理紧张;

(2)2023年比2022年相比,运算量大还是主弦律,这仍然是学生应试的最大痛点;

(3)2023年不按套路出牌,打破常规命题是一个亮点,数学问题切入点变化大且巧妙.

3.2重点模块与分值占比

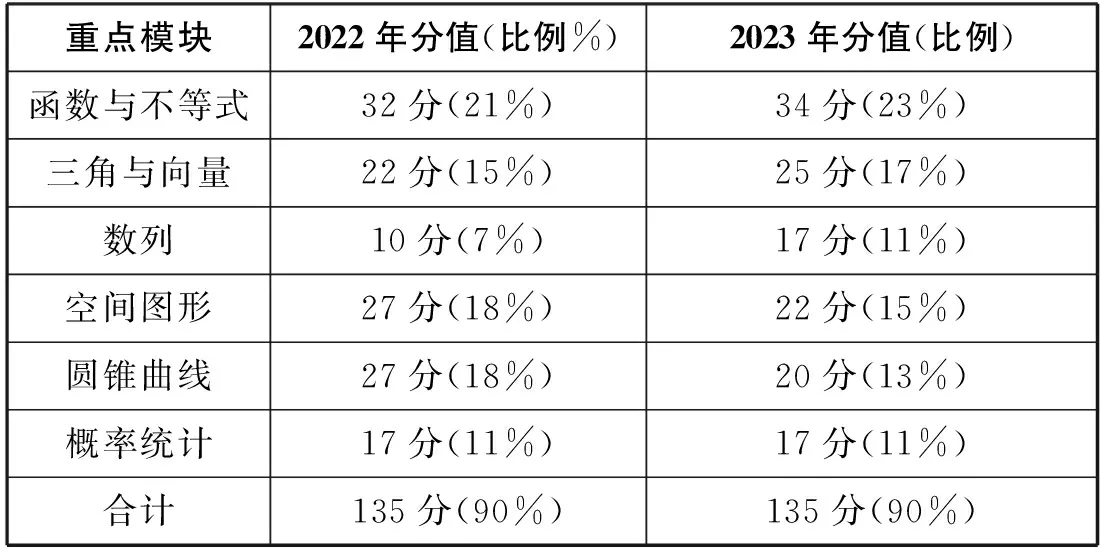
表3 2022年与2023年重点模块分值(以新高考数学全国卷1为例)

此表可以发现:

(1)2022年与2023年重点模块所占整卷比例九成,这是高三数学复习教学重要阵地;

(2)2023年函数、三角、向量与数列分值有所增加,概率统计保持不变.

二、新高考数学卷命题新动向

1.新考法——不按套路出牌,打破常规,创新命题思路

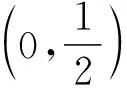
(Ⅰ)求W的方程;

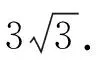
【分析】此题表象是圆锥曲线题,实质是函数导数题,矩形ABCD的周长为2(AB+BC),而AB与BC垂直,垂直的关键是两线段的斜率互为负倒数,即线段AB,BC的长是斜率k的函数,而且是复杂函数,为了研究其最小值需要导数工具来帮忙,使圆锥曲线中的运算,从简单的套路(初等代数运算),过渡到复杂函数的导数运算.

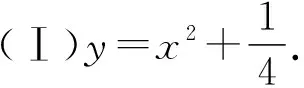
(Ⅱ)证明略.

2.创新题

客观性试题情境化命题,主观化测试.把客观性知识放在特定情境中,提高情境设置水平,让问题生长在数学情境中.

【例2】(2023·新课标Ⅰ卷·11T)已知函数f(x)的定义域为R,f(xy)=y2f(x)+x2f(y),则( )

A.f(0)=0

B.f(1)=0

C.f(x)是偶函数

D.x=0为f(x)的极小值点

【解析】前三个选项通过赋值易判其正确,而最后选项否定其正确性需要举反例:

作为应试:函数f(x)=0为常数函数,且满足f(xy)=y2f(x)+x2f(y),而常数函数没有极值点;

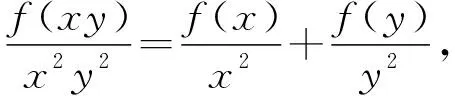
三、新高考数学卷命题之共性

1.现实情境

新高考数学命题均在现实情境(贴近学生生活环境)中挖掘,将数学教育“立德树人”落到实处,如新Ⅰ第21题挖掘体育中投篮比赛过程;新Ⅱ第3题体育运动统计调查;新Ⅱ第19题挖掘三年新冠传染背景,将现实情境与概率+函数紧密联系;上海第11题人上坡消耗的总体力问题,第19题汽车模型的外观与内饰颜色问题.

【例3】(2023·新课标Ⅱ卷·19T)某研究小组经过研究发现某种疾病的患病与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者与未患病者该指标的频率分布直方图:

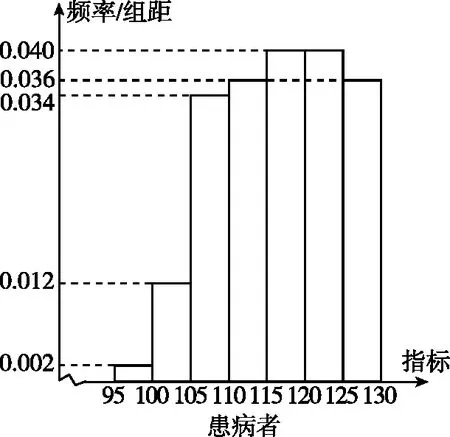
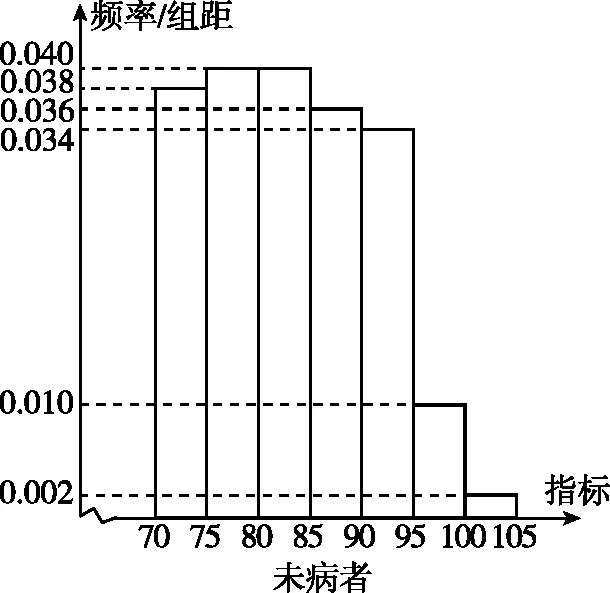
利用该指标制定一个检测标准,需要确定临界值c,将该指标大于c的人判定为阳性,小于或等于c的人判定为阴性,此检测标准的漏诊率是将患病者判定为阴性的概率,记为p(c);

误诊率是将未患病者判定为阳性的概率,记为q(c),假设数据在组内均匀分布,以事件发生的频率作为相应事件发生的概率,

(Ⅰ)当漏诊率p(c)=0.5%时,求临界值c和误诊率q(c);

(Ⅱ)设函数f(c)=p(c)+q(c),当c∈[95,105]时,求f(c)的解析式,并求f(c)在区间[95,105]的最小值.

【答案】(Ⅰ)c=97.5,q(c)=3.5%.

f(c)min=0.02.

【评析】此题将概率与分段函数有机结合,体现数学命题综合化趋势.

2.空间图形考法

新高考数学试卷均在“空间图形情境+问题”中深入挖掘,加大考查力度,保持2022年命题风格:新Ⅰ第12,14,18题;新Ⅱ第9,14,20题;上海第12,17题.

【例4】(2023·新课标Ⅰ卷·12T)下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有( )

A.直径为0.99 m的球体

B.所有棱长均为1.4 m的四面体

C.底面直径为0.01 m,高为1.8 m的圆柱体

D.底面直径为1.2 m,高为0.01 m的圆柱体

【答案】ABD

【评析】此命题把多面体与旋转体之间的位置关系以此角度巧妙挖掘展示,新颖别致,用数字说话.

3.核心模块

新高考数学试卷均在核心模块中挖掘,突出数学思维的本质特征,上述表三统计数据说明了这一点.

四、新高考数学复习备考建议

自2020年起,新高考数学全国卷逐步按照《普通高中数学课程标准》中的高考评价标准进行,从评价指导思想,评价内容,评价题型,命题情境等方面形成规范,以检测学生数学关键能力为先,数学主干核心知识保持稳定,在现实、科学、数学情境中深入挖掘数学模型,突出通过快速阅读来理解问题的数学本质,通过数字运算来解决问题模型,通过等价转化实现复杂情境向简单情境的转化.

1.牢牢抓住核心主干知识模块

(1)数学核心主干知识模块复习重在基本概念、基本方法、基本思想的训练,任何复杂情境和综合性问题最终落脚点都是上述三基;

(2)数学经典问题是数学复习的根,选择好的母题,通过变式推进将核心知识点展开,覆盖相关知识,形成知识模块;

(3)在核心主干知识中增加开放性命题训练,推进深度学习.

2.现实情境科学情境抓住模型

(1)现实情境训练强化三关,即事理关,明白问题中现实情境说了一件什么事,学会建模分析;文理关,即阅读理解关,一般现实情境的文字阅读量都比较大,通过阅读找出关键词和关键句,并理解其意义;数理关,对建立的数学模型,会用恰当的数学方法去解;

(2)科学情境挖掘数学模型,一般科学情境涉及到多学科知识综合,通常给出即时定义,只有快速理解情境中的学科知识的即时定义,才能准确建立起数学模型,此类训练是必须的.

3.关注运算和转化力软肋训练

(1)解决数学问题离不开数学运算,特别是分数、分式运算,解方程,解不等式,三角运算,向量运算,导数运算等,运算软肋是导致问题求解失败的第一杀手;

(2)复杂问题分解为简单问题离不开等价转化,特别是函数性质的等价转化.