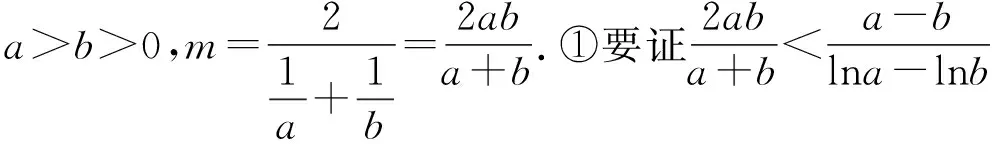洞悉趋势 融聚未来
——2023年创新仿真题多维分析选登(一)
杨 飞 陈 威 韦敏妍
(1.河北省献县第一中学;2.大连市第八中学;3.广西河池市民族高级中学)
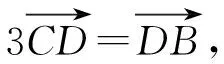

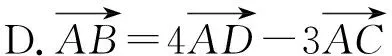
【答案】D
【考点】平面向量的线性运算



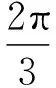


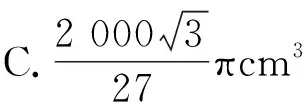
【答案】B
【考点】圆锥的体积公式
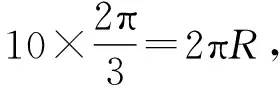
【高考风向】高考数学试题的背景素材会紧密联系国家社会经济发展、生产生活、科技发展以及数学文化等具体情境,以此考查考生在数学情境中运用数学思想、知识方法解决实际问题的能力以及数学应用的灵活性和创新性.
3.某大学生社会实践服务小分队的7名大学生志愿者(包括甲、乙两名大学生)要参加社区治理、邻里守望、社区环境保护三个课题的调查,每名同学只参加一个课题组,每个课题调查组至少两名同学,则甲、乙两名大学生没有被分到同一课题组的概率为( )
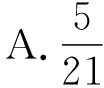
【答案】B
【考点】古典概型+排列与组合
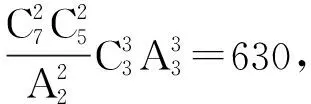

4.已知函数f(x)=x3-2ax2+a2x+b在x=1处取得极大值5,则( )
A.a=3,b=1
B.a=1,b=5
C.曲线y=f(x)在x=-1处的切线方程为24x-y+9=0
D.函数f(x)的图象关于点(2,3)对称
【答案】ACD
【考点】极值+导数的几何意义+函数图象的性质

【知识拓展】已知f′(x)为函数f(x)的导函数,令g(x)=f′(x),若方程g′(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.任何一个三次函数都有“拐点”,且“拐点”就是三次函数图象的对称中心.
【全能解析负责教师:杨 飞 河北省献县第一中学】
1.在数列{an}中,定义an为不大于n且与n互质的正整数的个数,则( )
A.{a2n}是递减数列 B.{a2n}是递增数列
C.{a2n}为等差数列 D.{a2n}为等比数列
【答案】D
【考点】数列的单调性+等比数列的定义
【全能解析】由题易得a2=1,a4=2,a6=2,所以数列{a2n}不是单调数列(提示:通过列举数列的前几项结合数列单调性的定义进行判断),故A,B错误;因为与2n互质的数为1,3,5,7,…,2n-3,2n-1,共有2n-1个,所以a2n=2n-1,则数列{a2n}为等比数列(提示:由等比数列的定义进行判定),C错误,D正确,故选D.
【高考风向】新定义试题是新高考的一种常考题型,在选择题中经常出现,由于题目新颖,信息丰富,可以较好地考查考生分析问题、解决问题的能力,考生需要认真阅读,理解题意,合理转化,进而解决问题.

A.中点 B.三等分点
C.四等分点 D.五等分点
【答案】C
【考点】几何体的外接球+球的截面性质
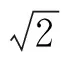

【方法技巧】解决球的截面问题关键在于合理使用球的截面的性质:(1)球的任意一个截面都是圆;(2)球的截面圆的圆心和球心的连线垂直于截面圆所在的平面;(3)球心到截面的距离d与球的半径R及截面圆的半径r的关系为R2=d2+r2.
3.已知经过点(-2,2)的两条直线l1,l2均与曲线y=x3+m相切,若直线l1的方程为y=2,则m的值为________,直线l2的方程为________.
【答案】2 27x-y+56=0
【考点】导数的几何意义
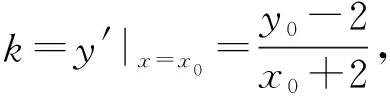
【高考风向】填空题设置多空试题是新高考的一大特点,有时还设置为开放性试题,可以培养考生的思维能力和核心素养.
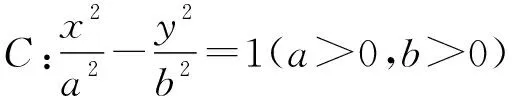
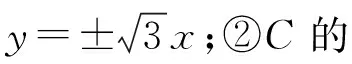
问题:求双曲线C的标准方程;
(Ⅱ)过点F2的直线l斜率为k,且与双曲线C交于D,E两点,直线A1D与直线A2E的交点为M,证明:在双曲线C上存在定点N,使得△MF1N的面积为定值.
【考点】双曲线的标准方程和几何性质+直线与双曲线的位置关系

【全能解析】(Ⅰ)若选①③,
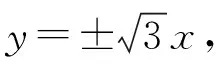

因为C上的点到焦点的最小距离为1,
所以c-a=1,


若选②③,
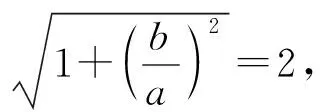

因为C上的点到焦点的最小距离为1,
所以c-a=1,


(Ⅱ)证法一:设点D(x1,y1),E(x2,y2),M(x0,y0),
由题意知,直线l不与双曲线C的渐近线平行,且斜率不为0,
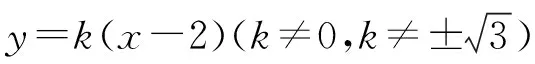

消去y并整理得
(3-k2)x2+4k2x-4k2-3=0,Δ>0,

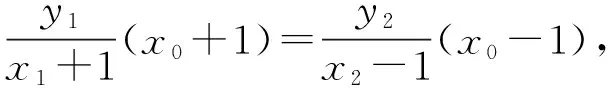

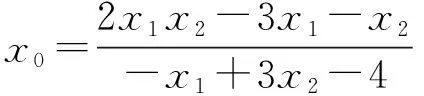
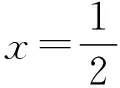
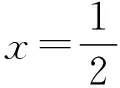
则点N的坐标为(-2,3)或(-2,-3),
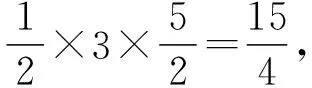
因此,在双曲线C上存在定点N,使得△MF1N的面积为定值.
证法二:设点D(x1,y1),E(x2,y2),M(x0,y0),
由题意知,直线l不与双曲线C的渐近线平行,且斜率不为0,
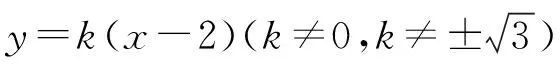

消去y并整理得
(3-k2)x2+4k2x-4k2-3=0,Δ>0,

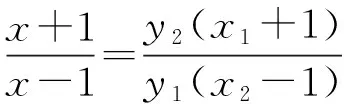


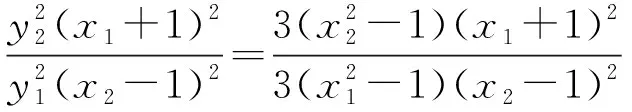

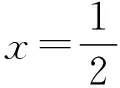
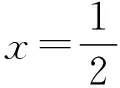
则点N的坐标为(-2,3)或(-2,-3),
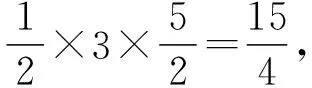
因此,在双曲线C上存在定点N,使得△MF1N的面积为定值.
【高考风向】解答题设置结构不良试题,是新高考的常考题型,可以培养考生的开放性思维.此外,挖掘隐含条件(定点、定直线等)也是高考压轴题的常设考点.
【全能解析负责教师:陈 威 大连市第八中学】
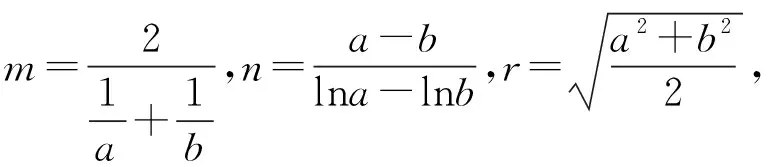
A.m C.n 【答案】A 【考点】利用导数研究函数的单调性 【全能解析负责教师:韦敏妍 广西河池市民族高级中学】