研究真题 把脉考向
——函数y=Asin(ωx+φ)中参数ω的取值范围问题
王敬全
(江苏省南京市溧水区第二高级中学)
函数y=Asin(ωx+φ)中参数ω的取值范围(最值)问题是近几年高考的高频考点及热点,2022年全国卷中有4道试题涉及ω的求值或范围问题,它与对称性、单调性、最值及零点(极值点)个数等相结合,综合考查函数性质,其中蕴含着核心素养、关键能力和必备知识,体现了高考试题的基础性、综合性和应用性,对学生的思维品质有着较高的要求.笔者整理了近年来全国卷中的这类考题,潜心研究解法、努力领悟立意、总结考查规律、预测考试方向,从而指导高三的复习备考.
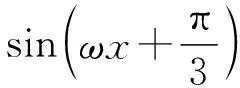


【解法1】这类问题往往以选择题的形式呈现,而选择题又可通过特殊值代入的方法求解.
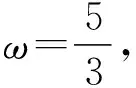
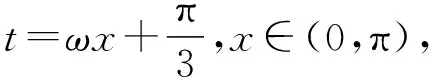

图1
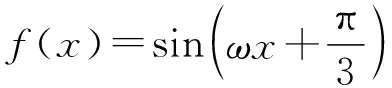

图2

【分析】该题考查三角函数的图象与性质,将函数的极值点和零点这两个函数的重要特征量进行有机的融合,解题过程中对数形结合、化归与转化等数学思想方法有着很高的要求,数学抽象、逻辑推理、几何直观、数学运算等数学学科核心素养得到了很好的体现.此题入口较宽,学生可以从不同的角度切入,体现了高考试题的开放性,对学生思维的严谨性也有很高的要求.
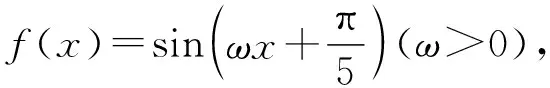
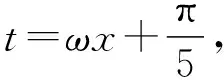

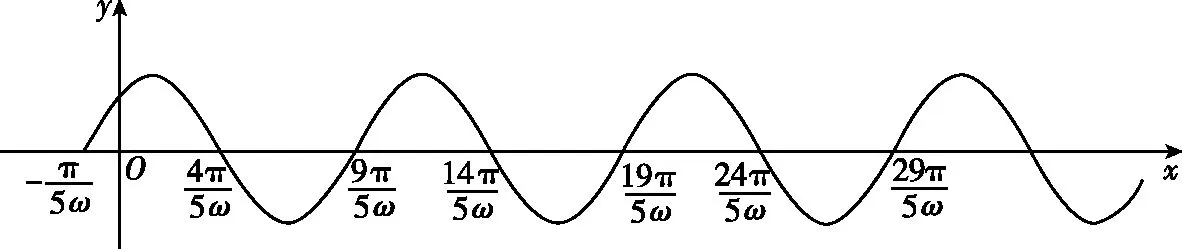
图3




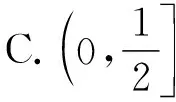


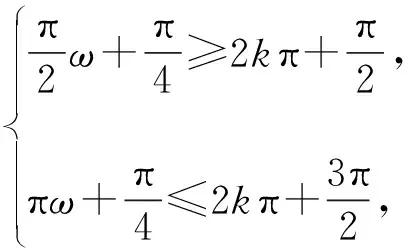
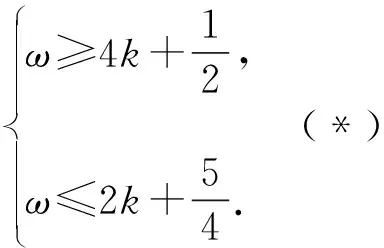

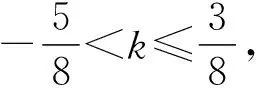

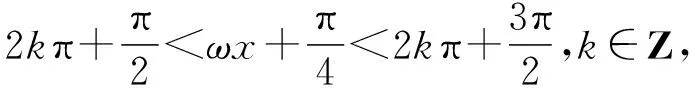

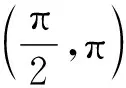
(下同解法2)
【分析】相对于例1和例2,例3所给的区间端点不是0,如采用换元法,新元t所在区间的两个端点均是变化的,无法确定它在正弦函数的哪个减区间中,难度陡增,只能考虑所有情况(用含k的区间表示),先根据ω有解,确定k的值(哪个区间的子集),然后求出ω的取值范围.
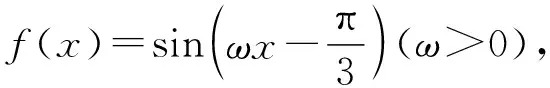

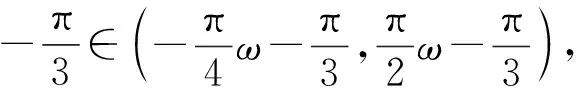
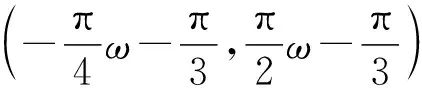
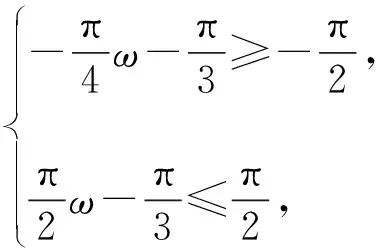
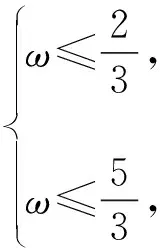

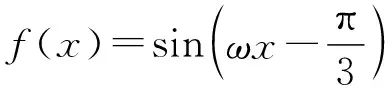

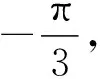

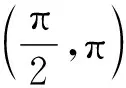
因为函数y=cosx的单调区间为(kπ,kπ+π),k∈Z,

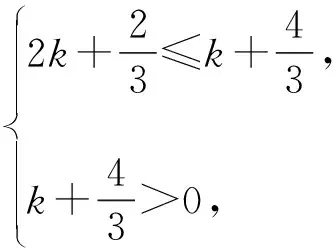
因为k∈Z,所以k=-1或k=0.
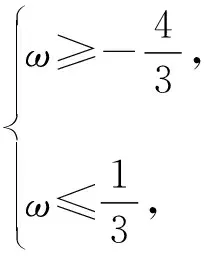
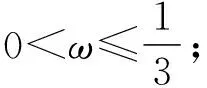
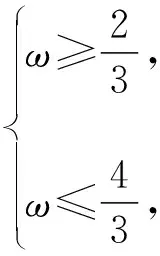
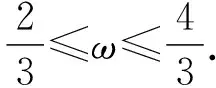

【分析】该题将函数的单调性以另一种形式呈现,转化为函数在给定区间上单调,由于所给区间中没有元素0,换元后新元t的区间两个端点均不固定,且区间中没有定值,难度加大.再加上是填空题,且是余弦函数,解决过程中还要分类讨论,学生得分情况不好,最终全区平均得分0.24分.
历年的高考题都是经过命题者精心打磨,立意、效度、信度都很高,且经过了高考的检验,科学性上有保证,有很强的导向性,是最权威的高考研究资料.作为一线教师及教研工作者,研究高考题应当成为一项常态工作,除了研究高考题的解法,更要研究其立意、背景、变式和导向,只有教师研究透了,才能领会命题者的意图,向学生讲清问题的本质,发挥试题的最大功能.事实上,高考命题从不回避陈题,很多试题都是“新瓶装旧酒”,因此教师需在已有考题的基础上,总结出这类问题的一般解法,尽可能多地想一想它还可能有的变化及考查方向,从而查漏补缺.

