解析初中数学因式分解运用思路

师三分

摘 要：初中数学的教学中，不论是分式，还是一元二次的方程，其相关运算都与因式分解有着密切关联.而十字相乘法更多是对二次三项的式子实施分解因式，还可以将其运用于一元二次方程、二次函数和x轴的交点坐标、二次不等式等求解中.由此可知，十字相乘法对于因式分解的问题解决有着显著帮助.

关键词：初中数学；因式分解；十字相乘法；运用思路

十字相乘法是对多项式实施因式分解的重要方法，其在中学数学的相关运算过程中通常有着重要作用.不论是初中阶段的数学教学，还是高中阶段的数学教学，因式分解都有着重要作用.部分试题中所提及的提公因式法以及公式法通常都无法实施分解因式，但是，通过十字相乘法实施因式分解，不仅有助于学生自身的思维拓展，而且还能使学生更便利地解决相关数学习题，从而使学生实现高效解题.

1 十字相乘法及其在因式分解中的作用

1.1 十字相乘法概述

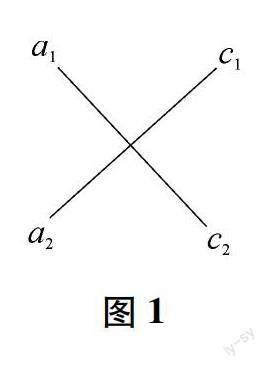
十字相乘法是通过画出十字交叉线进行系数分解，以此对二次三项式进行分解的方法.如图1所示，十字的左边两因数相乘与常数项相等，交叉相乘得出的结果进行相加，得出一次项系数，此时，二次三项式能够分解成两个多项式相乘的积.

若二次项的系数为负数，就能先将负号提到括号外，将二次项系数转变成正数，接着再实施因式分解；若二次项的系数为正数，可分两种情况探讨：情况1，二次项系数是1的二次三项式x²+bx+c，即把常数项c拆分为两个因数，即c₁与c₂，让这两个因数的乘积结果正好是常数c，且c₁与c₂二者的和则是一次项系数b.情况2，二次项的系数不是1的二次三项式子ax²+bx+c，也就是将二次项系数a与常数c分别拆为两个因数，即a₁与a₂、c₁與c₂，其中，a₁与a₂的乘积为a，c₁与c₂的乘积为c，且a₁和c₁或c₂当中的任一个进行相乘得出的积加剩余的因数相乘得出的积正好与一次项的系数b相等.

1.2 十字相乘法在因式分解中的作用

数学教材中因式分解的方法通常有两种，也就是提公因式法与公式法，就提公因式法来说，其通常属于多项式的因式进行分解时最为常用的方法，但不论是提公因式法，还是公式法，都有着较大局限性.其更多适合部分多项式，如x²-4x+4可通过平方公式分解成（x-2）²，但有些式子仅通过教材中的方法是无法分解出来的.例如，分解因式x²-3x+2，通过上述两种方法是无法分解的，而运用十字相乘法，则能对式子进行轻易分解，将其分解为（x-2）（x-1）.

2 以“十字相乘法”进行因式分解

2.1 二项式的平方差

2.1.1 一项是字母平方，一项是数字平方

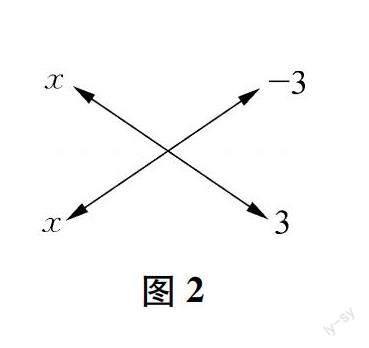
例1 分解因式x²-9.

解析：如图2，十字中的左边x和x相乘得到的结果是多项式第一项x²，右边-3和3相乘得到的结果则是多项式第二项-9.因此，x²-9=（x-3）（x+3）.

2.1.2 两项都是字母的平方

例2 分解因式x²-y².

解析：如图3，十字的左边为x和x，相乘得到的结果是多项式第一项x²，右边-y和y相乘得到的结果则是多项式第二项-y².因此，x²-y²=（x-y）（x+y）.

2.1.3 两项都是数字和字母的平方

例3 分解因式（9x）²-（4y）².

解析：如图4，十字的左边为3x和3x，相乘得到的结果是多项式第一项9x²，右边-2y和2y相乘得到的结果则是多项式第二项-4y².因此，（9x）²-（4y）²=（3x-2y）（3x+2y）.

2.2 三项式因式分解

2.2.1 三项可形成完全平方

例4 分解因式x²+6x+9.

解析：如图5，虽然该因式是完全平方的一个式子，但通过十字相乘法也能够有效分解，也就是分解二次项与常数项.十字的左边为x和x，相乘得到的结果是多项式第一项x²，右边3和3相乘得到的结果则是多项式常数项9，每条直线的两式子的乘积和是6x.因此，x²+6x+9=（x+3）（x-3）=（x+3）².同理，如果一次项系数为负数，就能把常数分为两个负的乘积.

2.2.2 三项包含二次项、一次项、常数项，一次项系数为1

例5 分解因式x²-6x+8.

解析：如图6，本因式主要是对二次项与常数项进行分解.十字的左边为x和x，相乘得到的结果是多项式第一项x²，右边-2和-4相乘得到的结果则是多项式常数项8，每条直线的两式子的乘积和是-6x.因此，x²-6x+8=（x-2）（x-4），常数分解的两个数的正负是由一次项系数正负所决定的.

2.2.3 三项包含二次项、一次项、常数项，一次项系数并非1

例6 分解因式2x²-3x+1.

解析：如图7，本因式主要是对二次项与常数项进行分解.十字的左边为2x和x，相乘得到的结果是多项式第一项2x²，右边-1和-1相乘得到的结果则是多项式常数项1，每条直线的两式子的乘积和是-3x.因此，2x²-3x+1=（2x-1）（x-1），一次项系数是由二次项系数与常数项所确定的.

2.2.4 三项都是二次项

例7 分解因式3x²+5xy+2y².

解析：如图8，本因式主要是对x和y的平方项进行分解.十字的左边为3x和x，相乘得到的结果是多项式第一项3x²，右边2y和y相乘得到的结果则是多项式常数项2y²，每条直线的两式子的乘积和是5xy.因此，3x²+5xy+2y²=（3x+2y）（x+y）.

2.3 多项式因式ax²+bxy+cy²+dx+ey+f分解

例8 分解因式3x²+5xy-2y²+x+9y-4.

解析：将多项式看作为xy的二次式，依据降幂，将式子整理成（3x²+5xy-2y²）+（x+9y）-4，再对前3项进行十字相乘，将十字相乘法的右边画为十字，将常数分解为2个因数，以此使2个因数位于第2个十字中的交叉乘积的和等于3x²+5xy-2y²+x+9y-4当中包含y的一次项系数，同时，和第1个十字左边的两个因数交叉的乘积和等于3x²+5xy-2y²+x+9y-4当中包含x的一次项系数，列出双十字相乘的图，如图9，3x²+5xy-2y²+x+9y-4=（3x-y+4）（x+2y-1）.

2.4 多项式因式ax²+bxy+cy²+dxz+eyz+fz²分解

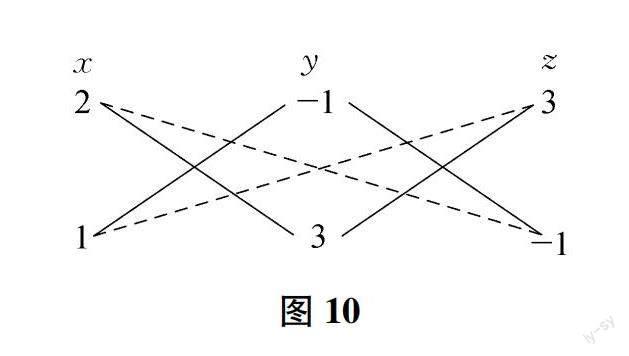
例9 分解因式2x²+5xy-3y²+xz+10yz-3z².

解析：依据十字列出双十字相乘的图，详见图10：

依据图10进行系数验证：

x²：2×1=2；

xy：2×3+1×（-1）=5；

y²：-1×3=-3；

xz：2×（-1）+1×3=1；

yz：-1×（-1）+3×3=10；

z²：3×（-1）=-3.

那么，2x²+5xy-3y²+xz+10yz-3z²=（2x-y+3z）（x+3y-z）.

3 结束语

综上所述，在初中数学的因式分解中运用十字相乘法，既能实现解题速度的加快，又能实现解题准确率的提高，从而使分式与一元二次方程在进行分解及相關问题解答时，能够实现问题的清晰化与简单化，并实现高效解题.