因式分解教学中的逆向思维培养

摘要：因式分解需要把一个多项式化为几个最简整式的积的形式，如果从运算角度上考虑，实际上就是把一个表示和的形式，改变式子的结构，写成乘积的形式，但要保持两者仍相等，这样的变形过程与整式乘法之间是互逆的关系.因式分解是进行逆向思维能力培养的最佳平台与载体，运用逆向思维不但可以使思考问题的过程显得真实化，还能培养学生解题的灵活性与创造性，培养积极探究数学问题的良好思维品质.

关键词：初中数学；因式分解；整式乘法；逆向思维

作者簡介：刘付强（1976-），男，江苏扬州人，本科，中学一级，主要从事初中数学教学研究.逆向思维是与正向思维方向相反的思维过程，但在思维内容上两者往往有一致性.在初中数学教学过程中，不少内容需要学生能够“反其道而思之”，使部分运用正向思维难以解决的问题得到顺利解决.比如要求学生画出一条长为5cm的线段，这里的思考过程就可以追溯到画直角三角形，如果直角边为整数，斜边有可能出现无理数的情况，经几次尝试探索就可以发现直角边为1cm与2cm的直角三角形，其斜边为5cm.

因式分解需要把一个多项式化为几个最简整式的积的形式，如果从运算角度上考虑，实际上就是把一个表示和的形式，改变式子的结构，写成乘积的形式，但要保持两者仍相等，这样的变形过程与整式乘法之间是互逆的关系.

一、由瓜找藤，理解公式的形成过程

因式分解的原理来自多项式乘法，比如（a+b）（a-b）=a2-b2和a2-b2=（a+b）（a-b）是一种逆向变形的关系.教学过程中，既要引导学生借助正向思维去获得公式，掌握其规律，也要让学生通过“瓜”来找“藤”，做到来去自如.

比如，对于提取公因式法的学习，教师可以这样操作：

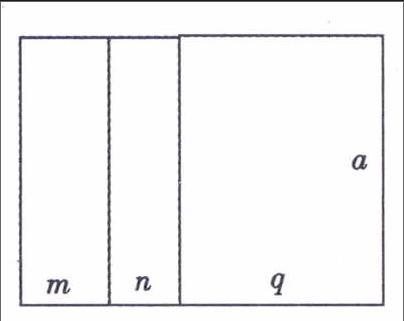
1.让学生写出：a（m+n+q）=am+an+aq，然后利用等式的特征写出am+an+aq=a（m+n+q）.

2.教师可以借助数形结合的方法展示如图，从而很快让学生理解：am+an+aq=a（m+n+q）

3.通过比喻的方式让记住这两个公式的表达形式：a（m+n+q）=am+an+aq——假如a前去某公司（括号正代表公司的房子）参观，正好遇到了过去的朋友m，n，q三人都在这家公司工作，于是a分别与这三人握手示好；am+an+aq=a（m+n+q）——握手并在这家公司办完事情后，a离开了这家公司，所以a已经在括号（公司）的外面了，而原来与他握手的三人还在括号里面.

4.计算25×4+25×34+25×2，在实践中理解这表示4个25相加，34个25相加，2个25相加，所以一共是40个25相加，与以原式等于40×25，这样就促进了理解.

5.归纳提取公因式法.

6.加强实战训练，尝试练习提取公因式法.

二、利用等式性质，作出逆向思考

从命题的角度分析，一个原命题的命题可以是真命题也可以是假命题，比如对于平方差公式：（a+b）（a-b）=a2-b2来说，它只是一种整式乘法的形式，表述成语言就是两数和与之两数差的乘积等于这两数的平方差，那么“如果两数写成平方差的形式，其结果是否等于两数之和与两数之差的积呢？”有的学生想当然地说这是成立的，理由呢，大家就会一踌莫展，而事实上，a=b成立，b=a就是成立的，用反证法也能证明它.学生就接触过这样的例子：因为︱5︱=5、︱-5︱=5，所以绝对值等于5的数有5与-5.但同样5=︱5︱还是成立的，这里要防止是的把调换两式位置两种情况与原逆命题混为一谈.比如对于平方差公式的思考方法：因为（a+b）（a-b）=a2-b2，所以等式a2-b2=（a+b）（a-b）右边部分等于a2-b2，与左边完全一样，所以a2-b2=（a+b）（a-b）成立.也可以运用反证法思考（学生还没有学习过，但其逻辑常识是早已被学生所接受的）：如果a2-b2≠（a+b）（a-b），那么根据（a+b）（a-b）=a2-b2，替换上以后出现a2-b2≠a2-b2的情况，这说明前边的假设是错误的，故a2-b2=（a+b）（a-b）.

三、借助数学思想，引导学生逆向思维

教学中往往对正向思维关注较多，由正向思维向逆向思维转移时，需要重新调整心理过程，重新建立心理过程的方向.由于初中因式分解解题过程中也会出现不少难题，光凭逆向思维往往不能解决问题，这时我们就需要适当运用一些手段，比如进行合理预设、运用一定的数学思想方法.解题过程中，教师可以引导学生进行一些假设，由于假设结论是成立的，然后由果查因，推导出原因也是成立的，这里我们往往需要用到添项与拆项的方法.

例如，对于“a2+b2+c2+29=6a+4b+8c，求a，b，c的值.”这一题，很多学生会无从入手，因为这是一个等式，而且题目中也没有明确规定或者提示解决问题的方法.

如何找到问题解决的切入点呢？首先可以把右边的三项全都移到左边进行观察，可以发现有三个字母，带这三个字母的项都有两项，那么就可以分成三类，即按三个字母分的三类：a2-6a，b2-4b，c2-8c.再观察a2-6a可以发现与平方差公式的运用很相似，这里第一项为a2，第二项-6a=2×（-3）×a，所以第三项最好是（-3）的平方，这样就需要通过补一个9来解决，最终就可以变形成（a-3）2+（b-4）2+（c-3）2=0，从而运用非负数之和为零，每项非负数均为零的性质得解.这种拆项与添项的方法在学生数学竞赛与课后的思考题中较多的出现，有助于培养学生的逆向思维能力和创新意识.

四、补充十字相乘方法，培养逆向思维品质

平方差公式与完全平方公式的逆用可以帮助学生进行因式分解，其实质还是建立在多项式乘以多项式的基础上的，而十字相乘法虽然近来并不作要求，但由于在实际数学问题解决中非常有用，而且有助于培养尖子生超前的思维能力，所以也十分有必要加以介绍，并引导学生尝试运用.比如对于a2-3a+2，学生如果通过配方的方法进行因式分解，会非常累，十字相乘在这儿就体现了它的优势.教学时，教师首先可以出些诸如“（a+1）（a+2），（a-3）（a+4），（2x+2）（3x-1）”的题让学生练习（在整式乘法部分教学时也需要适时教学），并尝试探究结果中一次项系数产生的规律，认识到这正是交叉相乘的积相加的结果.在因式分解过程中，同样可以运用十字相乘法进行，但这时学生就需要还原上述过程，进行逆向思考.当然，这些方法对学生的要求不是刚性的，鼓励学生多学习不同的方法虽有助提升解题的灵活性，但教学过程中不必强行超出教材要求，更不能加重学生负担.

五、回顾学习过程，寻找解题突破口

因式分解这块内容在教师看来是非常简单的，但事实上很多学生并不理解，练习过程中错误也会很多，其原因还在于教师引导不当，学生理解不透，所以加强与整式乘法的联系，不断加强由因找果与由果溯因的双向关联训练是非常必要的.另外，教师在训练难度设计上要逐渐加深，不能一步到位，否则易挫伤学生的积极性.对于一下子难以解决的问题，可以引导学生从前边所学的知识中激发解决问题的灵感.

比如对于运用整体思想的训练中的这样一道题a（x-y）+b（y-x），可以这么引导，因为（x-y）与（y-x）是相反数关系，可以通过提取第二个式子中的负号让两者相同，这样原式就化成了a（x-y）-b（x-y），我们把括号内看成一个整体，或者令x-y=M，原式就是aM-bM，正好可以把M提出来.其解题思路如下“aM-bM←a（x-y）-b（x-y）←a（x-y）+b（y-x）”，所以这里教师要做的是引导学生去找到这一题的前置性训练，唤起学习的经验.这是对平时问题学习过程的再回顾，也属于逆向思维.

总之，在数学教学过程中，教师必须培养学生的逆向思维能力，而因式分解是进行逆向思维能力培养的最佳平台与载体，运用逆向思维不但可以是思考问题的过程显得真实化，还能培养学生解题的灵活性与创造性，培养积极探究数学问题的良好思维品质.具体教学过程中，教师需要结合教学内容，引导学生挖掘有效的解题方法，不断唤醒学生的前期学习经验，做出理性科学的回顾，从而解决问题.

参考文献：

[1] 王平，王宏伟.运用辩证法分析新教改[J]. 读书文摘. 2016（18）

[2] 何卫群.把握已有教学资源，设计有效教学活动——“因式分解之十字相乘法”研究课题教学片断及思考[J]. 数学学习与研究. 2016（22）

2017年1月10日理科考试研究·物理版理科考试研究·物理版2017年1月10日