探讨平面几何图形面积计算的特殊方法
摘要:平面几何图形的面积计算是初中数学的重点和难点,教师在教学中要教会学生掌握“先往某个方向集中”、“超出多少就缩进多少”和“定理的特殊证明”等图形转换方法来解决问题,从而让学生感悟到图形的排除、包含、转化等重要数学思想.
关键词:平面几何图形;面积计算;特殊方法
作者简介:陈泽宁(1965-),男,汉族, 广东省台山市人, 大学学历,中学高级教师,台山市市管拔尖人才,台山市任远中学副校长,主要从事中学数学教学研究.平面几何图形的面积计算在初中数学教材中占有十分重要的地位,通过求平面几何图形面积的教学,能让学生掌握一些图形转换方法,感悟图形的排除、包含、转化等数学思想.而在教学过程中,平面几何图形面积计算的特殊计算是教与学中的一个难点,下面来谈谈三方种特殊的计算方法.
一、先往某个方向集中
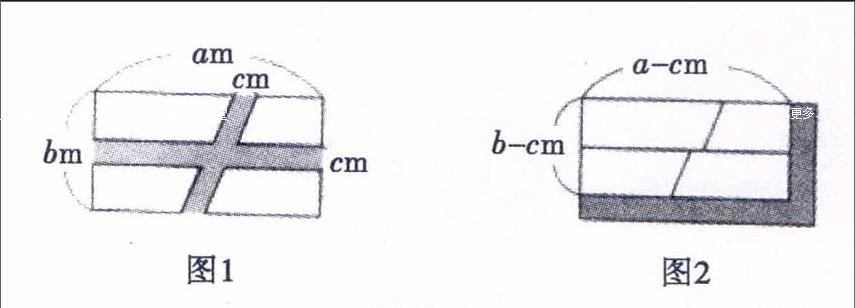
例1有一块长为a米,宽为b米的长方形宅地,在这片土地上造了如图1所示的两条道路,道路宽为c米.那么,请问土地的面积剩下多少平方米?
分析思维较肤浅的同学极易分别求出四个梯形面积之和,或用大矩形ABCD的面积减去阴影部分的面积.尽管也能计算出,但费时费力;思维较深刻的学生,掌握问题的本质:把去掉道路的土地往左靠拢,然后再往上靠拢,于是变成了没有道路的长方形,如图2的情形.这样,就可以很简单地算出剩下土地的面积.
解 S土地= (a-c) (b-c) = ab-ac一bc+c2 (平方米)
二、“超出多少就缩进多少”的原理
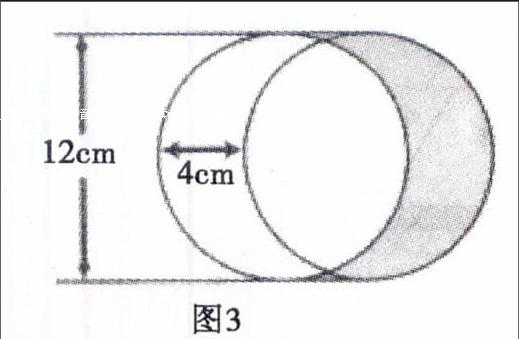
例2计算出图3中灰色部分的面积.
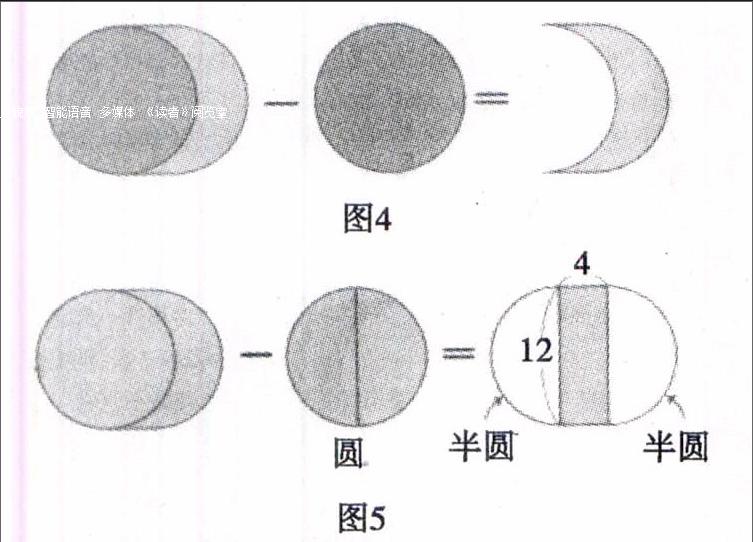
分析一按常规的思路,可能出现以下的解法,如图4所示,从整体面积中扣掉圆的面积,就是所求的面积.如果要扣掉圆的面积,那么就要按图5把圆切成两半后再扣掉也是一样.如此一来,就出现了一个长方形的面积.
解法一所求的面积为S=12cm×4cm = 48cm2
分析二由于原来的图形很难做判断,因此我们在圆上加了一个长方形,把它变成了如图6所示的图形.如果把这个图形左右各延伸4 cm,右侧会出现我们要计算的图形,而左侧就会出现一个长方形.我们可以这样来思考,也就是说右侧延伸出多少面积,左侧就会内缩多少面积,如图7所示.
解法二所求的面积为S=12cm×4cm = 48cm2
点评像以上这样,可以用不改变面积的方法把它变成容易计算的图形,题目中右侧类似月牙形状的部分,就以这种方式被巧妙地变成了左边的长方形.在数学里,把这种思考方式叫做“卡瓦列利原理”.
拓展所谓卡瓦列利原理,道理跟用来画出水管突出部分线段的取样绘图器是一样的,如图8所示.同学们可以根据这种情况来思考“超出多少就缩进多少”的原理.
三、勾股定理的特殊证明
例3图9中,直角三角形的三边长为a、b、c,则c2=a2+b2成立.
分析只要证明出“两个小正方形面积之和等于斜边的大正方形面积”, 则c2=a2+b2就可以成立.所以,在如图10所示,只要把正方形CBED变成长方形JBHK,再把正方形AFGC变形为长方形AJKI就行了.
证明下面证明正方形CBED变成长方形JBHK:
1.首先把正方形CBED切割成细细的长方形,然后,按照顺序移动,把它变成为平行四边形ABEL(从图10→图11).
2.B点不动,把这个平行四边形按顺时针方向方向旋转90°,变为平行四边形HBCM(图11→图12).
3.把平行四边形HBCM以另外的細长法切割(图13).
4.把细细的长方形按照顺序移动后,变形成为长方形JBHK(图13→图14).
以同样的方法,可以证明把正方形AFGC变形为长方形AJKI.
使用这种方法,也许有人会对长方形的锯齿部分非常在意.但只要把长方形不断变细,那么锯齿的部分就会逐渐消失.这跟以后学习的“极限、积分”中所讲的原理是一样的.
在整个初中学习中,类似这几类妙解的题目很多,同学们如果经常探讨巧解妙证,不但能锻炼自己的观察分析能力,促使思维敏捷,沟通不同知识的内在联系,有助于培养自己综合运用知识的能力和提高解题的技能与技巧,从而发展思维的创造性.
参考文献:
[1]钱建华.注重方法形成过程促进课堂智慧生成[J].中学教研(数学),2014(11):28-30.
[2]史宁中.数学教育的未来发展[J].数学教学,2014(1):1-3.
[3]刘东升,余中华.数学是怎样学好的(初中版)[M].长春,吉林教育出版社,2014:41.

