当平行线与角平分线邂逅会有怎样的精彩

摘要：平行线与角是初中几何中的基本图形，角的平分线在平面几何中具有重要的作用.本文通过典型例题对平行线与角平分线的结合进行了分析与探究，发现当平行线与角平分线在同一图形中出现时，不难得出相等的角或边的结论，用“平、平、等”三字概括此类几何图形中三者之间的微妙的关系.

关键词：平行线；角平分线；相等

作者简介：符布先（1985-），男，本科，中学二级教师，主要从事初中数学教学研究.在初中数学教学中，几何推理和图形证明是教学中的重难点，需要学生有良好的空间想象能力，很多学生感觉学习时很吃力，如果教师仍然采用照本宣科的教学方法，教学效果自然难尽人意.因此，发掘几何图形推理和证明中的规律性的技巧，对提高初中数学教学质量，有着积极的作用.

平行线的性质是初中几何的一个基本性质，可通过平行线的性质证明角之间的数量关系.角是初中几何中的一个基本图形，角的平分线所在的直线是角的对称轴，角的平分线在平面几何中具有重要的地位和作用.当平行线与角的平分线在同一图形中结合时，会有什么不一样的情况出现呢？

例1已知，如图1，在△ABC中，BD平分∠ABC交AC于D，DE∥BC交AB于E.证明：△BDE是等腰三角形.

分析题目中已知条件为BD平分∠ABC， DE∥BC，根据平行线的性质，可得同位角或者内错角相等，以及同旁内角互补，由角平分线的定义可知，∠ABD=∠CBD，利用等量代换可得在△BDE中，∠ABD=∠BDE，故△BDE为等腰三角形.

证明∵DE∥BC（已知）

∴∠EDB=∠DBC（两直线平行 内错角相等）

∵BD平分∠ABC（角平分线的定义）

∴∠ABD=∠BDE（等量代换）

∴△BDE是等腰三角形（等角对等边）

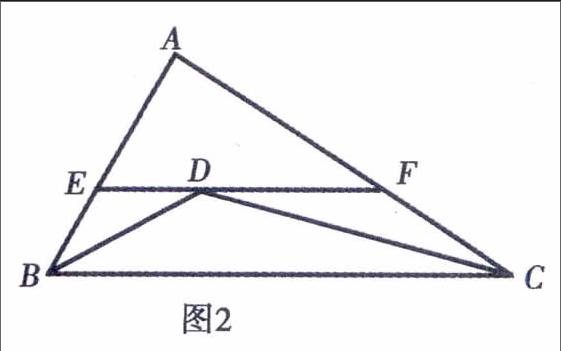
例2如图2，在△ABC中，AB=6，AC=8，BD平分∠ABC，CD平分∠ACB，过D作EF∥BC分别交AB、AC于E、F.求△AEF的周长.

分析此题中的图形在三角形章节中常出现，该题中的条件有EF∥BC、BD平分∠ABC、CD平分∠ACB，对比上面典型例题1，不难发现两者的联系，运用其可得BE=ED、DF=CF，故△AEF的周长可通过等量代换转换成AB+AC来计算得出.

解∵BD平分∠ABC，CD平分∠ACB

∴∠ABD=∠CBD， ∠ACD=∠BCD

∵EF∥BC

∴∠CBD=∠BDE， ∠BCD=∠FDC

∴∠ABD=∠EDB， ∠FDC=∠DCF

∴ED=BE，DF=CF

則△AEF的周长=AE+EF+AF

=AE+ED+DF+AF

=AB+AC=6+8=14

例3已知，如图3，AE是△ABC外角的平分线，且AE∥BC，求证：△ABC为等腰三角形.

分析等腰三角形可由两角相等或者两边相等来判定，在平行线间多有角的相等关系，在同一三角形中当两角相等即可得到两边相等，即该三角形为等腰三角形.

证明 ∵AE平分∠DAC（已知）

∴∠DAE=∠EAC（角平分线的定义）

∵AE∥BC（已知）

∴∠DAE=∠B，∠EAC=∠C（平行线的性质）

∴∠B=∠C（等量代换）

∴AB=AC（等角对等边）

即△ABC为等腰三角形

通过上述问题中对平行线与角平分线的结合进行了分析与探究，发现当平行线与角平分线在同一图形中出现时，往往不难得出，相等的角或者相等的边的结论，故我用“平、平、等”三字概括此类几何图形中三者之间的微妙的关系.

总之，在初中数学几何推理和图形证明中，教师需要引导学生认真观察几何图形，归纳解法及解题思路，从而提高学生几何证明的能力，实现教学相长的目的.