以『思维』为养料让学生自由生长———以《探索与发现：三角形内角和》为例

文|呙楚娇

《探索与发现：三角形内角和》一课选自北师大版四年级下册第三单元，其学习目标为探索三角形的内角和等于180°，让学生在探索发现的过程中体验数学思考和探究的乐趣。根据学情分析，大部分学生已然知晓三角形内角和是180°。在这样的情况下，作为教师我们到底要教给学生什么？笔者将以《探索与发现：三角形内角和》这一课前后两次导入和探究过程的教学设计来谈谈对“教什么”“怎么教”这两个问题的理解和设计。

一、教知识还教思维

数学到底教什么？数学教育有三个层面：第一层是把数学当作知识来教，第二层是把数学当作思维来教，最高境界是把数学当作文化来教。

1.（第一次导入设计）动画激趣，导入课题

播放动画：在三角形家族中似乎遇到了什么问题：“我的个头最大，我的内角和一定是最大的。”“我最胖，我的内角和才是最大的。”“爷爷，真的像它们说的那样，我的内角和是最小的吗？”“这可是三角形家族的秘密！”

师：你知道三角形家族的这个秘密吗？

生：它们的内角和是一样的，都是180°。

师：你们都同意他的想法吗？那在研究这个问题之前老师想先问问大家，什么是三角形的内角？什么是三角形的内角和？

生：三角形里面的角叫作三角形的内角。

师：你能上来指一指吗？（学生上台指出教师手上三角形的三个内角）

师：那什么是内角和呢？

生：三角形三个角加起来的度数就是内角和。

师：刚刚大家都认为三角形的内角和是180°，那我们就一起来看看它到底是不是180°。

2.（第二次导入设计）现实表演，探究争论

课件出示：“我比你大！”“你错了！你没有比我大！”“看起来就是我大！不信我们比比！”“比就比！”

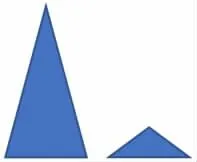
师：这两个三角形情绪这么激动，它们在比什么？

生1：它们在比谁的面积大。

生2：它们在比谁的周长长。

师：你们觉得呢？

生：周长和面积一眼就能比出来大小，所以不是比这些。

师：那它们在比什么呢？

生：它们可能在比角的大小。

师：比单个角的大小也很容易比，那还有什么要争的呢？

生：比三个角度数的和谁更大。

师：那到底谁的角度之和更大呢？为了方便大家的表达和比较，我们一起给这6 个角标上数字吧。像这样∠1 加∠2 加∠3 的角度之和就是这个三角形的内角和。

【对比分析】

第一次设计的动画导入，虽然画面色彩丰富，三角形的形象生动活泼、绘声绘色，但离学生的实际生活经验较远，无法引起学生的共鸣和认知冲突。站在学习科学认知负荷的角度上分析，色彩过于丰富、元素使用较多的画面更容易增加学生的外在认知负荷，使学生无法全心全意聚焦在讨论的问题里。而第二次的导入设计，只有两个最简单的三角形实物教具，为学生减少了非必要的认知负荷，再通过教师的生动表演，更能将学生的思维聚焦到三角形争论的内容上。

另外，从学生的学习心理出发，一二年级学生需要生动有趣色彩丰富的导入引起注意；三四年级学生则需要“有用”的导入，即与实际生活联系紧密，源于生活且能用于生活的情境；而五六年级学生则更喜欢具有挑战性，或者能够激发胜负欲、求知欲和探究兴趣的问题导入。本节课属于四年级下册的内容，学生的思维和学习心理已经在向五年级过渡和迁移，所以在导入情境的选择上要偏向于有挑战性，且能够激发他们探究欲望的问题和情境。对比第一次三角形内角和大小的争论后，引出“你知道三角形家族的这个秘密吗”的问题导入，第二次“它们到底在比什么”的开放性问题导入更能激发学生的好奇心和学习兴趣，特别是在“比周长、比面积”这两次回答被否定的情况下，学生的胜负欲立刻被激发，探究兴趣和求知欲望会更加强烈，从而全身心投入到本节课的探究中。

最后，回到“教什么”的问题。从学科本质来看，教师到底是教知识？还是教思维？还是教文化？如果是教知识，那么教师只需用讲授法将知识灌输给学生，让学生记住概念和方法。如果是教思维，那么教师需要通过提问题、探究活动、师生互动和生生互动去启发学生的思维，让学生经历自主思考和探究的过程，明白是什么、为什么和怎么用。当然，还有最高层次的教文化，这需要教师在教学中将跨学科跨文化的知识融合到极致，能用数学的眼光看任何事情，然后将其与数学知识概念勾连起来，提炼出其中的数学思想，最后再用数学语言将其表达出来，对学生进行数学思维文化上的熏陶。

二、是石头还是种子

在李政涛教授的《教育常识》一书里提到了“正确地做教育”则需要正确的“教育观念”，就是正确“看教育”之后形成的见解。而“看教育”中最重要的是“看学生”，教师如何看待学生，就会采用对应的教育教学方法。到底是将学生看作是罐子、石头或者是种子？两次探究设计中，笔者的学生观发生了明显的改变。

1.（第一次探究设计）动手操作，探究问题

（1）猜测。

师：现在请大家拿出学具，按照《学习单》上的内容和小组合作要求一起看看三角形的内角和到底是不是180°吧！

四人小组合作：

①四人为一个小组，每人拿一个不同的三角形。

②同伴间合作量一量、算一算，一人记录并完成表格。

③组内交流：你发现了什么？

姓名三角形的形状∠1 的度数∠2 的度数∠3 的度数三个内角的和/度

师：观察每个小组的内角和，你发现了什么？

生1：每个三角形的内角和都不一样。

生2：量出来的三角形内角和都不是180°。

师：为什么会这样呢？难道刚刚那个同学说的“三角形内角和都是180°”这个结论是错的吗？为什么有些三角形的内角和不是180°呢？

生：因为我们的测量会造成误差，所以算出来的结果基本都不是180°。

师：那三角形的内角和究竟是不是180°呢？

（2）验证。

师：在刚刚的活动中，我们发现尽管测量有误差，但是结果都接近于180°，那你有更加精确的方法证明三角形内角和一定是180°吗？

师：180°是什么角呢？

生：平角。

师：怎样让三角形上的三个角变成平角呢？

生：我们可以把三角形的三个角都撕下来，然后拼在一起，就能得到一个平角，所以它的内角和就是180°。

同桌两人合作探究，通过撕一撕、拼一拼、折一折，验证三角形内角和等于180°。

2.（第二次探究设计）小组合作，探究三角形内角度数之和

师：如何判断谁的内角和大呢？

生：可以先量出每个角度的度数，再计算出内角和比较大小。

同桌合作：

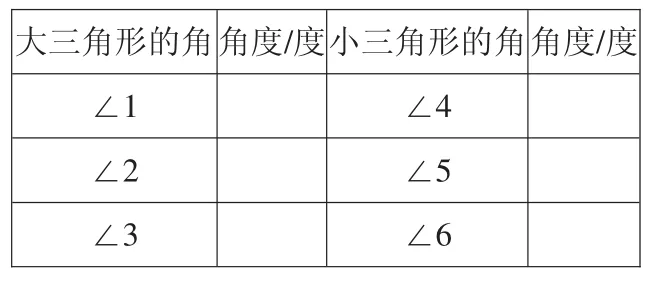
（1）从学具袋中拿出大小三角形，一人选择一个三角形，测量出每个内角的角度，记录在《学习单》的表格上。

（2）选几组同学上台输入测量结果（电脑自动求和）。

?

探究结果：从数据得到的三角形内角和有178°、179°、180°、181°……

师：为什么会出现这样的情况？

生：测量时会出现误差，有的时候量得不准确。

师：既然用量的方法无法准确判断出哪个三角形的内角和比较大，你们还有其他的方法吗？

四人小组合作：

利用学具袋中的大小三角形和直角三角形、锐角三角形、钝角三角形各两个，小组内想办法探究三角形内角和是不是180°。

小组合作汇报：

生1：将直角三角形的两个锐角撕下来，可以拼成一个直角，两个直角加起来就是180°。

生2：将两个一模一样的直角三角形拼成一个长方形，因为长方形的四个角都是直角，内角和等于360°，那一个三角形的内角和就是180°。

师：直角三角形是相对特殊的三角形，那怎么验证锐角三角形和钝角三角形的内角和是多少呢？

生3：将三角形的三个角撕下来，借助直尺发现三个角拼起来刚好可以拼成一个平角，从而得到三角形的内角和是180°。

生4：将三个角对折，发现三个角刚好可以拼在一起，拼凑成一个平角，从而得到三角形的内角和是180°。

小结：三角形的内角和都是180°，所以这两个大小三角形的内角和是一样大的。

【对比分析】

本节课是一节典型的探究学习型课，在教学过程中要注重引导学生参与探究活动，经历发现问题、解决问题和建构知识、运用知识的过程，让认识基于实践，通过实践得到提升。

通过试教，不难发现第一次的探究设计探究性不够，提出的问题开放性和思考性都较低，并不能真正激发学生的探究欲望。而第二次探究设计以两个问题为教学主线“如何判断谁的内角和大呢？”“有什么方法可以验证你们的想法呢？”以问题驱动学生的学习兴趣和自主探究欲望，给足学生自主思考探究和实践的空间，让学生充分表达自己的观点，发挥想象力，积极主动地参与探究活动，提升学生发现问题、提出问题、分析问题、解决问题的能力，体会到自主探究的乐趣和挑战性，使学生人人有发展，人人有收获，最终使学生的数学核心素养得到发展。

作为教师，应该“怎么教”，其实这取决于怎么看待学生。如果将学生看作罐子，那我们只需要用最简单的方式往里面倒知识，填鸭式地将其灌满即可；如果将学生看作石头，我们会对其精雕细琢，把其雕刻成我们想要的样子，但他们没有自己的想法和思维，被动接受我们的方法和思想；但如果我们将学生看成种子，我们要做的是给其提供一片合适的土壤，施以水和肥料，然后静待其自由生长，最终靠其自己的力量长成想要的样子。在第一次探究设计中，因为低估了学生的探究能力，不断地将自己的思路和方法强加给学生，不仅提供了“平角”的脚手架，还将其思维限制在“撕一撕、拼一拼、折一折”的思维框架中，现在回忆起来，就是把学生看成了一块石头，努力将其雕刻成笔者想要的样子。而第二次的探究设计，学生这颗种子在笔者提供的这块宽阔而无限制的土地上，通过平等的师生、生生交流和多维的互动，对“如何证明三角形内角和是180°”这个问题进行深入探究讨论，在讨论和汇报展示中努力吸取养分，最终积累了向上生长的力量。

三、课后总结

教学是促进学生生长的过程，而不是最终的结果，我们在教学中应该更加注重给学生养分，让其靠自己的力量找到学习的价值和意义，而不是单纯地将三角形内角和等于180°这个结论告诉他们。所以在开放性问题的驱动下，学生自发地去寻找解决问题的方案，主动参与到教学活动中，积极探究，从而促进学生核心素养的发展，培养学生用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界的能力。

其实教学相长，教学不但促进了学生的发展，也促进了教师的成长。本节课笔者经历“思考——设计——反思——再设计”的教学设计过程，在过程中深刻地体会到一节课的设计不能局限于数学知识本身，应该跳出数学学科的框架，从多个角度来分析一节课中的所有环节，树立起正确的学科观和教学观，最终做到“授之以鱼，不如授之以渔”。