用问题引领 促规律探索——《多边形的内角和》教学设计与思考（一）

文|刘萍萍

【教学内容】

苏教版四年级下册第96、97 页。

【教学过程】

一、基于经验，提出问题

师：回忆一下，我们是怎样得到三角形内角和的？

生：用量角器量出三个角的度数相加得到三角形的内角和是180°。

生：把三角形的三个角撕下来拼在一起，发现其内角和是180°。

师：知道了三角形的内角和是180°，你能想到什么问题呢？

生：四边形、五边形、六边形的内角和是多少？多边形的内角和有没有什么规律？多边形的内角和是怎样计算的……

师：大家提出的问题都很有研究价值。今天我们一起研究“多边形的内角和”。

【设计意图：学生经历过三角形内角和的探索过程，激活学生的旧知，在交流中启发学生提出问题，用问题引导学生进行“多边形的内角和”的规律探索活动。不仅明确了本课活动的目标，更激发了学生参与探索活动的积极性。】

二、尝试研究，明确方法

1.探索任意四边形的内角和

（1）自主探究

师：想先研究哪个多边形？

生：四边形，因为它的边数少。

师：从简单情况想起，很好。谁能大胆猜测一下四边形的内角和？

生：四边形的内角和是360°，因为长方形和正方形都是四边形，它们的四个角都是直角，四个角的和是360°。

生：但长方形和正方形是特殊的四边形，它们是360°，也不能说明所有的四边形都是360°。

师：是啊，一般的四边形是不是360°呢？大家可以根据研究要求自主研究。

（2）汇报交流

生1：我们组是用量一量的方法研究的。我们分别测出手中四边形的四个角是30°、150°、30°、150°，加起来就是360°。

生2：我们组是用拼一拼的方法研究的。我们把四边形的四个角全部剪下来，刚好能拼成一个周角，也就是360°。

生3：我们组是用分一分的方法研究的。我们把四边形分成两个三角形，因为每个三角形的内角和是180°，两个180°就是360°，所以这个四边形的内角和是360°。

师：听明白了吗？有什么疑问？

生：明明是两个三角形的内角和，为什么又是四边形的内角和？

师：问得真好！谁能在图上描一描、画一画，回答这个问题呢？

生：大家看（出示图1），∠1、∠2、∠3 是一个三角形的三个内角，∠4、∠5、∠6 是另一个三角形的三个内角，这六个角的和正好是四边形的内角和。

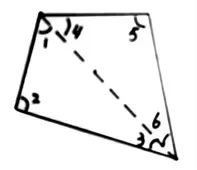
图1

师：你是怎么想到把四边形分成两个三角形的？

生：三角形的内角和为180°是我们学习过的知识，因此，我就想能不能将四边形转化成三角形来思考，于是就将四边形分成了两个三角形，没想到真的可以。

【设计意图：先让学生独立自主地进行方法探索，出现不同的方法都是“原生态”的思考。基于已有的知识经验，在前面的学习中积累了求“三角形的内角和”的学习经验，且多次进行过用三角形拼四边形或把四边形分成两个三角形的活动。因此，在操作及交流启发下学生想到测量角度、剪拼内角、分割为两个三角形求和等计算四边形的内角和的方法。再经过交流、比较，学生对多种方法的认识会提升一个台阶，发现不同方法的优劣，从而优化方法，并思考后续问题的解决，可以为后面的高效探索服务。】

2.探索任意五边形的内角和

（1）迁移方法，展示研究

师：下面你们想研究哪个图形的内角和？准备怎么研究？

生：研究五边形的内角和，可以把它分成几个三角形进行研究。

生1：从顶点开始（如图2），把五边形分成三个三角形，三个三角形的内角和就是五边形的内角和。

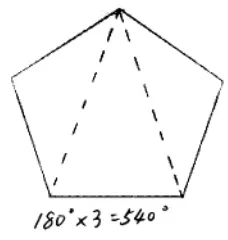
图2

生2：我从五边形内找一点进行分割（如图3），五边形被分成五个三角形，要计算五边形的内角和，还要把中间这个周角减掉。

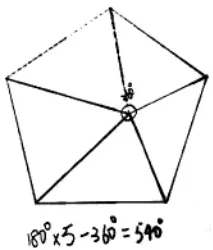
图3

师：为什么要把周角减掉？

生2：因为这个周角不是五边形的内角。

生3：我从边上找了一点分割（如图4），把五边形分成了四个三角形。这四个角组成的平角不是五边形的内角，所以要减掉180°。

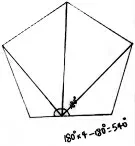
图4

（2）比较方法，提升认知

师：刚刚同学们用不同的分法都探究出了五边形的内角和，有什么相同的地方？

生：都是分成了三角形，通过三角形的内角和计算出五边形的内角和，都是540°。

师：探究四边形的内角和时，大家用了不同的方法，为什么现在大家不约而同地选择用“分三角形”的方法？

生：测量法会有误差，而且角越多误差就越大；撕拼法比较费时间，也不太方便；把四边形分割成三角形后计算，简单又方便。

生：三角形的内角和我们已经知道了，所以只要通过分一分、算一算就能知道五边形的内角和。

师：看来，我们要善于用好已经得出的规律去探索新的问题。那么，同样是“分三角形”，这几个作品又有什么不一样呢？

生：分法不同，分成的三角形的个数也不同。

生：我喜欢第一种分法，分出的几个三角形的内角和正好是五边形的内角和。第二种、第三种分法分出的三角形的内角中，有的不是原来五边形的内角，所以后面还要减去，有些麻烦。

生：从顶点出发分三角形不会出现多余的角，计算比较简便。

【设计意图：“分三角形”的方法是学生自我感悟而得，更真实。而把一个五边形分成方便计算内角和的三角形，部分学生可能存在一定的困难。因此先让学生自主探索，再组织交流，了解不同的分法。教学中给学生足够的时间对自己的研究方法进行交流、讨论，在对比中优化。这样，全体学生参与活动，经历了知识的发生发展的过程，体现了学习的主体性。同时，避免部分学生在探索过程中成为“看客”和“听众”。】

三、深入研究，发现规律

1.互相合作，填表整理

出示要求：

（1）选择一个多边形分一分，算一算。

（2）组内交流你的发现。

（3）汇总数据，填写表格。

2.观察表格，发现规律

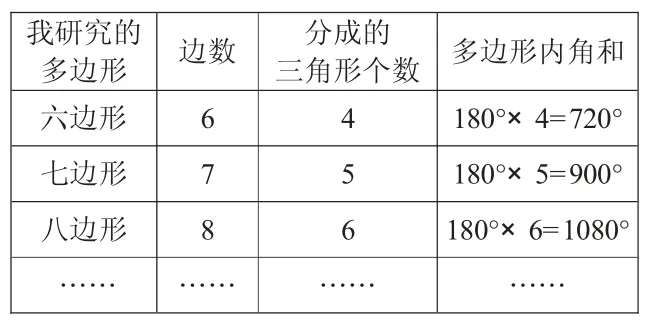
我研究的多边形边数分成的三角形个数 多边形内角和六边形64180°×4=720°七边形75180°×5=900°八边形86180°×6=1080°……………………

师：观察表格，你有什么发现？

生：我发现分成的三角形的个数越多，内角和也就越大。

生：我发现内角和就是分成的三角形的个数乘180°。

生：我发现分成的三角形的个数比多边形的边数少2。

师：为什么分成的三角形的个数比多边形的边数少“2”呢？请同学们观察图形想一想。

生：因为从多边形的一点出发，它不能与自己相邻的两个点连线，所以分成的三角形个数比边数少2。

3.归纳总结，建构模型

师：你能用一个式子表示多边形内角和的计算方法吗？

生：多边形的内角和=180°×（边数－2）。

生：多边形的内角和=180°×（n－2）。

师：这里的n 表示什么？

生：多边形的边数。

【设计意图：引导学生以小组合作的形式，把任意的多边形分成几个三角形，计算每个多边形的内角和，并列表整理所获得的数据，学生经历了探索、发现规律的过程。接着启发学生观察表中的数据，发现规律。在交流中帮助学生理清思路，发现计算多边形内角和的基本方法，获得一般性的规律。发现规律后，启发学生用一个式子把所发现的规律表示出来，帮助学生初步体验数学表达的严谨性和简洁性。】

四、回顾反思，沟通联系

1.回顾总结，交流体会

师：在探索和发现规律的过程中，你有哪些经验要分享？

生：把多边形分成三角形，可以推算出它们的内角和。

生：从四边形、五边形、六边形开始想起，多边形的边数越来越多，但规律是相同的。

生：n 边形的内角和=180°×（n－2）。

2.立体切换，多维沟通

师：用乘法分配律将多边形的内角和公式变一变，180°×（边数－2）=180°×边数-180°×2=180°×边数-360°，你又有什么发现？

生：从多边形中间任一点出发，几边形就可以分割成几个三角形，但内角和多一个周角，所以减去360°才是原多边形的内角和。

生：从多边形边上任意一点出发分割，分出的三角形比边数少“1”，同时还多出了一个平角，所以原图形的内角和是180°×（边数-1）-180°=180°×边数-360°=180°×（边数-2）。

师：根据“多边形内角和=180°×（边数-2）”这个规律，你能提出什么问题考考伙伴呢？

生：二十边形的内角和是多少？

生：有没有内角和是1000°的多边形？

【设计意图：通过经验分享让学生主动回顾总结。在反思、交流中，帮助学生进一步整理在探索多边形内角和计算方法过程中积累的经验，感悟类比、归纳、转化等思想方法，发展初步的问题意识、探索意识和创新意识。本环节没有将目标局限在探究出多边形内角和的通用公式，而是通过乘法分配律沟通多种分割方法之间的联系，学生深刻体会到分割方法的多样性和数学结论的一般性，提升观察、比较、归纳等多项能力。】

【教学反思】

亚里士多德说“思维自疑问和惊奇开始”。数学过程是一个不断发现问题、分析问题、解决问题的动态化过程。好的问题能诱发学生的学习动机、启迪思维、激发求知欲和创造欲。

1.问题引领学习

课始，学生在回顾三角形内角和的学习过程的基础上，教师以问题启思考，激发学生产生探索多边形内角和的学习需求，从而以饱满的热情投入到探索与研究之中。此外，在探索规律时，引导学生遵循一般的由简入难的规律，从四边形、五边形到其他多边形的探索，随着数学思维的不断进阶，学生能够持续保持探究兴趣。

2.发展模型意识

《义务教育数学课程标准（2022年版）》在“模型意识”里指出：“数学模型可以用来解决一类问题，是数学应用的基本途径。”课堂中，首先探索四边形的内角和时，学生经历自主研究的过程，独立研究出度量法、剪拼法、分割法等不同的方法，体会到了数学探究方法的多样性，并在交流中将方法优化。接着，在探索五边形内角和时，学生虽然都使用了分割法来进行研究，但是方法各不相同，教师尊重学生的个性化思维，适时引导学生加以理解。最后在总结环节，借助乘法分配律这一知识将学生的几种不同分割方法进行有效串联，更有效帮助学生认识数学方法间的内在联系，有助于学生初步形成模型意识，提高学习数学的兴趣和应用意识。