立足基本事实 展开数学推理——以特级教师朱国荣《三角形的三边关系》一课为例

文|黄 建

随着《义务教育数学课程标准（2022年版）》的颁布，其中一些变化的内容引起了教师们的关注。如：强调基于基本事实形成数学意识，关注尺规作图等。在小学阶段，基本事实主要有：两点间线段最短、等量的等量相等、等式的基本性质。哪些内容的教学要基于基本事实？如何开展基于基本事实的教学呢？前不久有幸聆听了特级教师朱国荣《三角形的三边关系》一课，深受启发。

片断一：创设生活情境，明确基本事实

1.创设情境，解决问题

师：图1中的直线l 表示一条河，点A、B 表示两个村庄。在何处架桥才能使A 村到B 村的路程最短？

图1

生：可以在点A、B 上画条线，与河的交点就是桥。

师：你们同意吗？

2.质疑反思，感悟关系

师：难道在点C 上架桥（如图2），路程就不是最短吗？

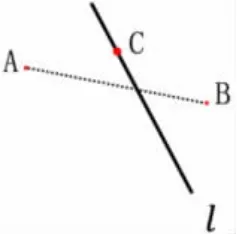
图2

生：这和跑步比赛一样，从C走就相当于走了弯路，距离更长。

师：如果从A 开始到C 还要拐个弯到B，那么这两条加起来就会比AB 要长，可以用算式表示：AC+CB＞AB。这就是我们刚才得出的结论，两点之间线段最短。

3.多维例证，得出基本事实

师：小明家到学校有三条路可走（见图3），如果他没有特殊情况，会走哪一条路？

图3

生：第②条路。它是直线段，是最近的。

师：两点间线段最短这个道理小狗也知道。如果在小狗面前放一根骨头，小狗会怎么跑过去？

生：小狗肯定是直的过去。

师：这样的道理我们可以给它一个名称，叫作基本事实。有了基本事实有什么用？今天我们借助基本事实来研究三角形三条边长度之间的关系。

【赏析：此片断聚焦基本事实的建立。主要有三个亮点：1.在背景方面，从生活中解决问题入手，感悟基本事实来源于生活；2.在内涵层面，引导学生对基本事实进行质疑与反思，借助算式对基本事实进行解释；3.在例证方面，与生活中的其他例子进行沟通联系，进一步体会基本事实与生活的密切联系。】

片断二：立足基本事实，理清三边规律

1.任务驱动

（1）画：请在白纸上画一个任意大小的三角形，建议画的大一点。

（2）标：用a、b、c 分别表示三条边的长度（标在每条边的中间）。

（3）探：联系“两点间线段最短”这一基本事实，研究三条边长度之间的关系。

2.四人小组合作

3.全班交流

（1）将三条边的长短进行比较

生：三角形有三条边，而且这三条边都是线段。它们中总有一条边是最长的，有一条边是最短的。其中a 最长。

生：我画的是b 最长。

生：我画的三角形的三条边一样长。

师：看来不是所有人的发现都一样。那它能否成为一个规律？

生：不能。

（2）关注三边长度关系

生：最短的和中间长的加起来一定大于最长的。

生：不同意，我画的三角形三条边一样长，没有最短的。

生：你虽然没有最长、最短的边，但是三条边也有这样的规律。

师：它们之间有什么关系？

生：a+b＞c。

师：不管a、b、c 中有长有短，还是三条边一样长，一定是大于吗？

生：如果三条边一样长，都是1，1+1=2 肯定比1 大。

生：我们知道两点间线段最短，c 看成一条线段，那么a+b 就不是线段，一定大于c。

师：他已经在联系基本事实了，你们听懂了吗？可以结合图进一步理解（如图4）。你能结合图说说为什么不用量就知道a+b＞c 吗？

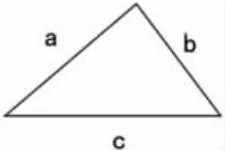
图4

生：可以看成从一个点到另一个点的连线，c 是线段，a+b 不是直线段。

师：你们画的三角形也有这个规律吗？与同桌说一说为什么会有这个规律。还有什么发现？

生：我发现除了a+b＞c，还有a+c＞b，b+c＞a。

（3）归纳得出三角形的三边关系

师：通过刚才的研究，我们发现不管什么样的三角形，三条边的长度之间有什么关系？

生：三角形任意两边之和大于第三边。

师：我们是根据这个基本事实（两点间线段最短）得到了这样的规律：三角形任意两边之和大于第三边。

【赏析：本环节以推理任务进行驱动，引导学生从形到数，再从数的角度分析、对比、归纳得出三边关系。教师引导学生从独立的三边长短关系走向关联的三边关系。主要有以下做法：首先，明确不是所有发现都符合的不能成为规律。接着，引导学生突破边的特征，立足一般例子得到其中的一组关系。学生通过举例、联系基本事实说明其中的道理。最后，从一组关系类比到三组关系，从一个图形迁移到多个图形，体会三角形三边关系的一般性。学生经历了根据基本事实得到规律的过程，体会到数学推理的角度与方法。】

片断三：结合尺规作图，优化判断方法

1.利用三边关系，判断是否可以围成三角形

师：知道了这个规律有什么用？请你判断，图5中哪组能够围成三角形？

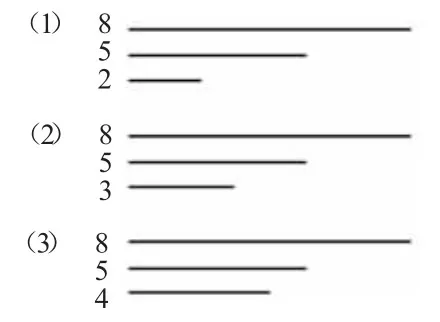
图5

判断下面每组中三条线段能否围成三角形？（单位：cm）

（1）理解“任意”

生：我觉得第一组不能围成三角形。因为8 厘米那么长，2 厘米那么短。如果2 厘米、5 厘米在两边，8 厘米在最下面，肯定围不成。

生：我不同意。8+5=13，13 大于2，它肯定能围成三角形。

生：是的！还可以说8+2＞5。

师：他们找到了两组关系，为什么你们还是说这三条边不能围成三角形呢？

生：因为最长边是8，剩下两边之和等于7，怎么围都不可能把这三边弄在一起。2+5=7，7＜8。

师：现在是一个小于两个大于，你们觉得能不能围成三角形？

生：因为刚才说要任意两条边大于第三边。这里的任意就是说这三个算式都要满足。

（2）优化方法

生：第二组也不可以，因为5+3=8，所以三条边不能围成三角形。

师：他觉得一组是等于，其他的两个算式就不用写了，有道理吗？

生：因为一组算式不符合要求，就不满足“任意”。

生：我觉得第三组可以围成。因为5+4＞8，5+8＞4，4+8＞5。

生：我觉得只要写一个算式就好了：5+4＞8。

师：为什么只要写一个算式？

生：因为连最短的两条边的和都大于第三条边了，如果是一条最长的边加另一条边，一定大于中等的或者最短的边。

师：经过研究，你有什么发现？

生：在判断的时候，只要看较短的两边之和是否大于第三边。

2.画三角形，由数构形

（1）初次尝试，直尺画图，讨论难点

师：这个三角形到底长什么样？请同学们把它画下来。

（学生操作，发现不容易画出三角形）

师：你遇到了什么困难？

生：我发现画了第二条边后，连接第三条边的时候不一定是我们想要的长度。

师：看来画一条8 厘米的线段、再画一条5 厘米的线段是很容易的。但是一下子凑准4 厘米很不容易。那有什么办法呢？

生：可以把第二条边的角度换一下。只要多画几次，就可以找到。

（2）工具迭代，突破难点，再次尝试

师：同学们，光有这把尺还不行，要有一个新工具——圆规来帮助我们画三角形。（播放视频）

3.应用工具，以形解数

师：刚才我们发现前面两组不能围成三角形。那用圆规画画看，会出现什么情况？

【赏析：有基本事实与规律后，本环节重在应用。从以下三个层次展开：层次一，利用规律判断三条线段是否可以围成三角形，理解“任意”即“所有”之后，在判断中优化方法，通过推理明确方法的可行性。层次二，尺规作图，体会三角形三边关系的本质就是两点间的距离：即找到一个交点，使得它到两个端点的距离分别是5 厘米、4 厘米。层次三，应用工具，反思规律。进一步明确当不符合任意两边大于第三边时，即找不到交点或者交点在线段上，从而不能围成三角形。本环节从数的计算出发，结合形理解计算的原理，实现了数与形的互译。同时，构建了基本事实—规律—方法的完整推理过程。】

【全文赏析】

聚焦推理，朱老师在课堂中非常关注以下三点。

一、立足生活，构建推理“前提”

数学的产生与发展始于对生活现象的观察、推理，但又不停留于此，需要进一步通过分析、抽象、概括去解释生活现象的本质。朱老师引导学生对生活问题“在何处架桥才能使A 村到B 村的路程最短”进行分析，通过正例、反例感悟几条线段之间的长短关系。有了关系的感悟，再次在多个情境中进行验证，逐渐抽象出本质关系。最后，概括得出基本事实——两点间线段最短，为推理奠定基础。朱老师不是将多个生活例子进行简单的叠加，而是精选材料并且合理利用材料。

二、基于操作，把握推理“结构”

推理，不仅反映前提与结论在内容上的关联，还体现在前提与结论于形式结构上的一致性。学生推理时，最大的困难在于把一组或者几组关系判断当作推理。

课堂中，学生的推理经历了以下几个阶段。前结构推理：即在一个三角形中，将各条边的长度进行比较，无法确定规律。单点结构推理：建立三条边之间的关系，但是关系不太稳固，如：只能说明在等腰三角形中存在两边之和大于第三边。多点结构推理：建立稳固的三边关系，如：能突破三角形的类型限制，推广到一般情况。

我们也感受到三个阶段之间的跨度大，大部分学生无所适从。是否可以进一步细化材料，如在任务二中，将“画”改为“选”。材料一：引导学生进行测量，从量的角度发现三边关系；材料二：体会线段的任意性以及推理方法多样性；材料三：自主创造。此环节，拉长推理时间，逐渐把握推理结构。

三、多维应用，优化推理“结论”

结论的“再推理”。一方面体现在从一般关系出发，推理得出特殊关系“较短的两边之和大于第三边”。另一方面，借助尺规作图让结论“可视化”，结合图形进一步理解结论，提升推理意识的同时，发展几何直观。