凸显本质 促进统计意义的理解——《平均数》教学设计与评析

文|吴玉兰 刘 璨

“平均数”是小学阶段要学习的重要统计量，能代表一组数据的整体水平。生活中的许多现象都需要用平均数来进行解释说理，一些实际问题也需要用平均数来解决。学生虽然在学习这一知识前对平均数已有所了解，但更关注如何计算平均数，因而忽视了平均数的统计意义。因此，在教学这一内容时，更需要突出平均数的本质，理解它的统计意义，感受数据蕴含的信息，能用合适的方法分析数据，形成一定的数据意识。

【教学过程】

一、整体感知，“创生”平均数

1.情境引入，选择代表数

我们学校的同学都很喜欢运动，体育老师统计了一下，发现喜欢篮球的同学最多。所以，体育组准备开展年级篮球赛。我们班的小黄同学很想参加，想去自我推荐。为了让老师更好地了解自己的水平，提高入选的可能性，他特意在放学后练习了一分钟投篮，还记录了投中的数量，我们一起来看一下。

小黄一分钟投篮投中数量统计表

为了大家看起来更方便，我把小黄的投篮情况做成了统计图。

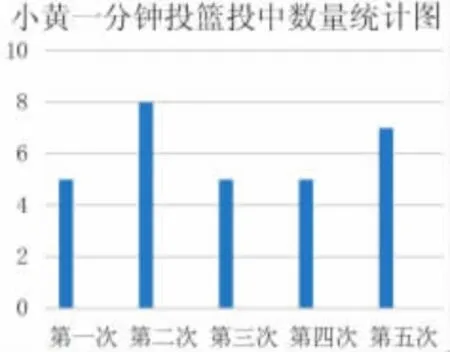
师：如果你是小黄，你打算用哪个数来表示你的一分钟投篮水平？把你的选择和理由轻轻地说给同桌听一听。

生：我选5，因为5 出现的次数最多。

生：我选8，因为8 是最好成绩，可以让老师觉得小黄很厉害。

生：但是小黄不是经常能投中8 个，万一下次投不中8 个了呢？所以我觉得应该选他的平均数6 个。（教师板书平均数）

2.说明解释，理解平均数

师：什么是平均数？能解释一下吗？

生：平均数=总个数÷次数，所以只要把所有投中的个数加起来除以5 就行了。

师：能列式吗？

生：（5+8+5+5+7）÷5=6（个）。

师：这位同学先求出所有投中的总个数，再平均分给每一次求出平均数，用“先合再分”的方法得到了小黄平均每次投中的个数。有不同的方法吗？

生：我是从第二次里面拿出一个给第一次，再拿出一个给第三次，然后从最后一次里拿出一个给第四次，这样每次都变成6 个了。

师：谁听明白了？

生：他是从个数多的里面拿出几个来分给少的。

师：我们一起来看一下刚才大家所说的变化过程（动画演示移多补少）。像这样从多的里面拿出一些给少的，我们也可以说是“移多补少”。

3.引发矛盾，体会虚拟性

师：刚才同学们用“先合再分”和“移多补少”两种方法得到了小黄平均每次投中的个数是6，但是这个数量小黄并没有投到，能代表他的投篮水平吗？

生：我觉得可以，因为平均分以后每次就6 个了。

生：我也觉得可以，因为平均数可以代表他的整体水平。

师：看来平均数虽然是虚拟的，不一定真实存在，但可以代表整体水平。

（板书：虚拟 代表整体水平）

【评析：“平均数”是生活中常见的统计量。因此，本环节从学生熟悉的场景引入，选择一个数据代表自己的投篮水平，引发产生平均数的必要性。同时，通过解释平均数的得到方法，感知移多补少，并体会平均数虽然是一个虚拟的数，却能代表整体水平，初步感知平均数的统计意义。】

二、操作探究，领会平均数

1.操作中体会平均数的代表性

（1）提出问题：我们班还有两个同学也很想参加，也拿着自己一分钟投篮的数据去自我推荐。但是除去班里校篮球队的成员，只剩两个名额了。如果你们是这个班的同学，会推荐谁去参加呢？

?

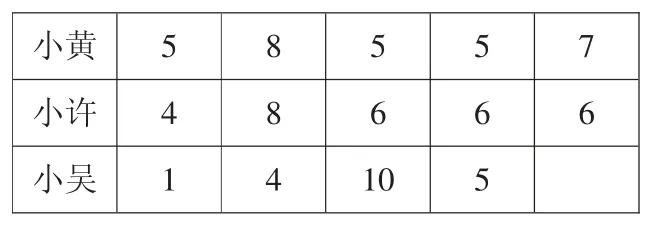
（2）操作研究。

①想一想：用哪个数代表小许和小吴的水平比较合适？可以在图中画一画，也可以算一算。

②选一选：推荐哪两个同学参加篮球比赛？说一说理由。

（3）小组交流：四人小组中说明各自推荐的理由；推荐一人代表小组汇报。

（4）全班交流。

师：哪个组愿意来分享研究成果？

生：我们是先合再分的，小许是（4+8+6+6+6）÷5=6（个），小吴是（1+4+10+5）÷4=5（个），所以我们推荐小黄和小许参加比赛。

生：我们组用移多补少的方法，发现小许平均每次投中6 个，小吴平均每次投中5 个，所以我们也推荐小黄和小许去参加比赛。

师：同学们不仅推荐出了参赛人员，还能用自己的方法说明理由，真好！我们来看一下你们的想法（课件演示移多补少的过程，并在课件中展示平均线的位置）。演示完后将平均线上移、下移，追问：表示平均数的线会不会在这里？为什么？——指出平均数大于最小值，小于最高值。

2.变化中感悟平均数的敏感性

（1）提出问题。

师：小吴落选了，但他很不甘心，你们知道为什么吗？

生：其他两个同学都投了5 次，他只投了4 次，不公平。万一他下一次投了很多个呢？

（2）操作解决。

师：老师很善解人意，又给了小吴一次一分钟投篮的机会，并给他定了三个目标：5 个、6 个、8 个。你觉得哪个目标能让他反败为胜？先猜，再在活动纸上画一画验证。

（学生纷纷猜8 个）

学生操作完以后交流反馈。

生：5 个不用考虑，因为小吴原来每次平均投5个，这次还是5 个的话，不会改变平均数；6 个也不会反超，因为虽然增加了一个，但这一个平均分给5次，每次一个都不到，平均数是5 个多一点点；8 个也不行，多出来的3 个也不够分，所以平均数还是不到6 个。

（根据学生描述出示统计图）

师：想知道小吴最终投了几个吗？（出示数据：10个）现在他的平均成绩是多少？

生：6 个。

师：怎么一下子就高了？

生：因为他的最后一次投中很多，给自己留6 个，多出来的4 个能补给前几次，每次正好一个，这样平均成绩就从5 个变成6 个了。

生：我觉得平均数会受某一次成绩的影响。即使前面不怎么好，如果最后一次很好，平均数也有可能超越其他人。

师：确实平均数很容易受某次成绩的影响，非常敏感。（板书：敏感 易受极端值影响）

师：现在三人的平均成绩相同，那你们推荐谁呢？

生：我想推荐小吴和小许。因为小许比较稳定，经常能投6 个，小吴能投高分。

生：我还是推荐小黄和小许。虽然小吴投了两次10 个，但他成绩不稳定，参加比赛还是稳定更重要。

师：看来，平均数只能给我们提供一定的参考，我们还需要结合其他的因素作出决定。

【评析：在知道“什么是平均数”“平均数是怎么得到的”基础上，本环节让学生借助条形统计图来解释说理，在画一画的过程中进一步领会“平均数介于最大值与最小值之间”“平均数具有一定的敏感性，容易受极端分值的影响”“平均数能帮我们作出判断，但不一定是决定性因素”……这样的教学流程使学生跳出平均数的算术意义，促进平均数统计意义的理解。同时感悟数据是蕴含信息的，我们能用数据来描述生活中的现象，数据能帮我们作出判断与决策，增强数据意识。】

三、联系生活，体会应用性

1.生活中你听说过平均数吗？

2.任选一份学习材料研究说理（独立思考后同桌交流，再全班汇报）。

材料一：一分钟跳绳，每人测4 次，佳佳的平均成绩是183 个/分；慧慧的平均成绩是186 个/分。判断下列说法是否正确，并说一说理由。

（1）慧慧第一次跳绳的个数一定比佳佳多。

（2）慧慧跳绳的整体水平比佳佳高。

（3）佳佳一定有一次跳绳的个数是183 个。

材料二：迪迪所在的五（1）班同学的平均身高是1.36 米，佳佳所在的五（2）班同学的平均身高是1.32米。判断下列说法是否正确，并说一说理由。

（1）迪迪一定比佳佳长得高。

（2）总体上来说，五（1）班同学比五（2）班同学长得高。

（3）如果五（1）班有一个同学的身高是1.40 米（1.40=1.36+0.04），那么这个班一定有一个同学的身高是1.32 米（1.32=1.36-0.04）。

材料三：国家统计局曾经发布中国人平均寿命大约是75 岁。74 岁的王奶奶看了这个新闻后，忧心忡忡，饭也吃不下，睡也睡不着。你想对王奶奶说什么？

3.课堂小结：这节课研究了什么？现在你对平均数有哪些了解？

【评析：《数学课程标准（2022年版）》指出，培养学生的核心素养，主要包含以下三个方面：会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。本环节提供了生活中真实存在的三个现象，引导学生从数学的角度去分析人文现象背后的数学原理，用数学知识描述、解释现实生活中的实际问题，促进核心素养的发展。】