聚焦关键问题 创新作业设计——数学核心素养视角下小学数学作业设计例谈

文|陈春兰

作业美好的样子，应该是同一个问题，让不同学生经历不同的过程，展示不同的结果；不同类型的作业，可以让不同学生都有体验成就感的机会。作业设计中存在的问题：忽略学情实际，不能激发学生的学习兴趣，促进学生的真正发展。在创新作业时，过度追求形式上的好看、好玩，由此造成作业内容本质被架空，无法达成作业存在的育人目标。对于作业设计缺少整体的规划与统筹，其中不乏出现一些交叉重复的内容。作业创新应该具有重要的育人价值，只有经过系统规划、精心设计、有效整合，才能真正发挥作业的育人功能，切实减轻学生的学业负担，让学生在丰富多样的作业体验中发展核心素养，健康快乐地成长。

在“素养”背景下，如何聚焦教材中的核心问题，创新作业设计，发挥作业的多方面功能和作用，笔者尝试从作业的“内涵”和“深度”两个方面进行探析。

一、多维视角，丰富作业的“内涵”

基于《数学课程标准（2022年版）》评价相关要求，以学生的发展为本，致力于培养学生的核心素养，既考查知识的形成过程，又考查学生在知识建构中能力的发展和素养的形成；既注重培养学生的问题解决能力，又注重培养学生良好的数学思想和数学探究的基本活动经验。

1.渗透思想，提升素养

学生在作业中结合线段图，列举了三种情况：第一种情况，当绳长为1 米时，剪去它的做蝴蝶结，还剩米；剪去米捆扎礼盒，剩下的也是米，故当绳长为1 米时，两根剩下的长度相同。第二种情况，当绳长为2 米（大于1米）时，剪去它的做蝴蝶结，还剩1 米；剪去米捆扎礼盒，剩下米，故当绳长大于1 米时，第二根剩下的长度长。第三种情况，当绳长为0.8 米（小于1 米）时，剪去它的做蝴蝶结，还剩0.4 米；而如果剪去米捆扎礼盒，剩下的是0.3 米，故当绳长小于1 米时，第一根剩下的长度长。学生通过数形结合，在对比、辨析中形象直观地解释了为什么“无法确定剩下的部分哪根长”的道理，进一步理解了分数的意义，通过数形结合，提升了数学素养。

2.放飞思维，提升能力

开放性的、一题多解的作业，可以调动学生追求成功的潜在动机，鼓励学生从多角度、多因果、多方面、多渠道探索解决问题的方法，培养学生的应用意识和创新意识。

作业呈现：

方案1

方案2

方案3

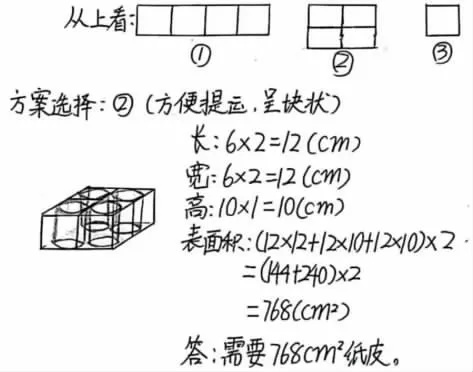
方案4

这道题让学生自由设计，题中符合要求的纸箱不只一种，具有一定的开放性、创新性。学生可以联系生活实际，根据自己的需求，从饮料瓶的不同摆放位置去考虑，设计心目中的纸箱。学生设计的纸箱有的有盖，有的无盖，有的学生还能从节省材料、便于搬运等多个角度来考虑。通过这种一题多解的作业，打开学生思维的阀门，当学生的思维不受限，灵感将会如泉水般喷涌而出，创新也就应运而生，素养的提升也就水到渠成。

3.设计分层，尊重差异

有关心理学研究表明：把选择权下放给学生，学生拥有了控制感，就更能调动学习的内驱力。所以，同一个问题情境，可以从不同角度、不同层次进行设计，让学生自主选择。

第一个问题是给定范围，要求设计两个不同的图形；第二个问题是规定数据，增加条件，要求设计三个不同的图形。通过对比，发现这两个问题的思维难度是不同的。通过这样的分层作业，既能让大部分学生巩固基础知识，又能让学有余力的学生进一步拓展和提升数学思维。学生在自己的最近发展区内自主选择作业，更能促进“不同的人在数学上得到不同的发展，逐步形成适应终身发展需要的核心素养”。

二、实践探究，挖掘作业的“深度”

适当提高应用性、探究性和综合性题目的比例，实现对核心素养的考查，这是核心素养导向下单元整体教学的需要。为此，在作业设计时，要根据教学内容及学生已有的数学学习经验，设计具有一定探究性的问题，引导学生通过口头说理、动手操作等多种探究形式，让学生成为一个乐于思考的研究者。

1.“说”——指向知识本源

教学中发现，有相当部分学生“会做题”，但不一定会思考、会说理，但“会说理”一定会思考、会做题。只有当学生会讲明道理、说清思路时，才是真正理解。

我们可以结合数学知识中的核心问题，设计口头说理的作业：“淘气学了长方体的体积后，不知道为什么长方体的体积＝长×宽×高？如果给你12 个同样大小的小正方体，你能解释为什么吗？请试着说明理由，可以把你的思考过程拍成小视频，分享到省教育资源平台人人通空间的‘活动广场’，与小伙伴进行交流。”

学生在“说”的过程中，“理”清了知识的来龙去脉，即长方体的体积就是“体积单位的累加，数一数有几个这样的体积单位”。凸显了知识的本质，加深了对数学知识的理解。

2.“放”——指向思维发展

思考是人类智慧的一种形式，也是人生学习的一种动力。数学学习离不开思考，具有独立思考能力是学好数学最基本的要求。作业中设计具有思考价值的问题显得尤为重要，一个好的问题要能引发学生的深度思考，具有一定的开放性，且能有效促进学生的思维发展。如下题：

学生作品：

（1）正例法。即周长越长，面积越大。如下图：

（2）反例法。即周长越长，面积可能相等，也可能越小。如下图：

这样富有挑战性的问题，既能满足学生好奇、好胜的心理，激发他们的探究欲，又能引导学生深入理解数学，体验思考的乐趣，自主建构知识。

3.“做”——指向素养落地

在一次毕业考试中，有这样一道题：“一个正方体的盒子，要得到它的平面展开图，需要剪开几条棱？”这道题的正确率不高，可能是学生在平时的学习中缺乏动手操作经验，也可能是学生动手操作中“做、思”分离，没有在做中“悟”。在教学正方体的展开图时，可以设计以下的课堂作业，引导学生剪一剪，再想一想，由单纯的动手操作，走向数学本质的体悟，实现思维的进阶。

实践表明，学生在操作、观察、思考中，既认识了正方体展开与折叠时各个面之间的对应关系，又发现了“得到平面展开图，需要剪开7 条棱”的秘密，学生的空间观念及空间想象能力得到了发展，并促进了素养的落地和思维的提升。

有效的作业设计需要坚持素养立意，凸显育人导向，要关注数学的本质，丰富作业的内涵，挖掘作业的深度，让学生自主探索、思考探究、动手实践，帮助学生巩固知识和方法，拓宽学习的空间，提升发现问题、解决问题的能力，形成和发展核心素养，为学生的终身学习奠定良好的思维品质。