从“浅层默会”到“深度建构”：优化小数初步认识的思考与实践

文|盛文雅

一、巧用默会，具物建构

创设现实情境，引入带具体单位的小数，启用并深化学生具体实物层次的认知储备，为操作说明做好铺垫。

1.启默会：借量识数

课伊始，大家一起阅读一篇学生自己写的数学日记：

我和爸爸一起去买菜。我记了账：爸爸买了15 个鸡蛋共30.8元，还买了一根甘蔗。这根甘蔗好长，卖甘蔗的说大约有2.4 米长，我的身高大约1.47 米，高出我好多啊。这根甘蔗打完电子秤后是12.85 元。我们一共花了0.5 小时买完了菜。

观察日记中的数，并分类，从表征形式上，知道小数是带有小数点的，接着尝试认读小数。通过圈一圈钱币，了解用整数30 元不够付，用31 元来付，钱又多出来，用小数30.8 元支付刚好。借助米尺认识2.4 米，通过比划长短，发现用整数表示有不够准确的困难，可以用小数表示。

总结起来，学生对小数的发生有了初步的印象：随着计量的精确，产生了用小数表征的需要，不足1 的那部分，可以用小数点后面的数来表示。

2.调经验：桥式架构

要更深入地认识小数，则必须借助操作，架构起小数与分数之间的桥梁。

以研究0.8 元为主任务，学习流程设计见图1。

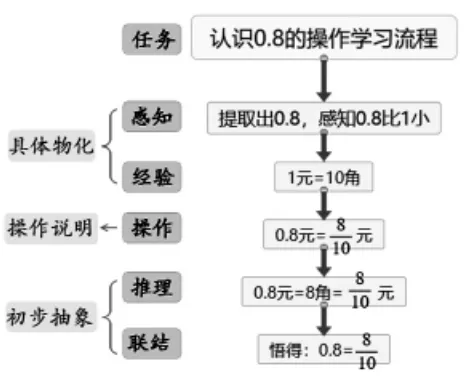
图1

【情节回放】

圈30.8 元的币值时，学生发现比30 元多0.8 元。

师：你能用框一框的方式来说明一下0.8 元为什么比1 元小，它和1 元又有怎样的关系呢？

学生尝试用10 个格子框住角币（见图2），表示1 元就是10个1 角，8 角占了其中的8 格（不足1 元）。

图2

师：刚才这位同学的操作过程就是我们以前学的什么知识？

这一过程是通过实物操作并演示来达成的，学生感知到0.8=之后用相同的学习流程，又分析了2.4 米表示的意义，明确了0.4 米=米=4 分米的道理，展开实物操作的过程，并步步配以准确的数学表达，克服学生原认知中模糊的地方，落实小数与分数、小数与整数的关系，建构小数的意义。

二、多元表征，操作建构

概念的掌握需经历一个从具体到表象再到抽象的过程。通过改变单位，进行多元表征，便于学生进行对比，概括出本质属性。

1.借直观：形中悟数

运用面积模型、线段模型、集合模型等直观手段解释小数的意义，并在“形”的对比中，抽象出共同属性，即小数单位与“1”之间的关系。

【情节回放】

（1）独立探究0.4。

师：如果把0.4 米改成0.4 千克，你打算如何表示它的大小？请同学们说一说、画一画、写一写。

（2）集体反馈交流。

4 位同学展示了自己的作品（见图3）并分别作出了说明。

图3

师：这4 位同学说的和0.4 米有共同的地方吗？

生：它们都是把一样物品平均分成10 份，其中的4 份表示0.4，也就是

2.集数轴：串式感序

在数轴上表示小数，进一步抽象小数的意义，使小数及其表征融入到整个有理数的系统中。

设计了把已学过的小数“请”到数轴上的教学环节，把实物和图形中表示过的一位小数，进一步表征到数轴上，之后，又数出了其他一些小数，逐步形成图4。为小数排序：数轴的上面是小数，下面是对应的分数，便于学生观察发现：一位小数都可以表示为分母是10 的分数；从1 份数到9份，即从0.1 数到0.9；关联小数的符号书写意义：不足“1”的部分，是把“1”进行十等分后的再计量，小数点后的数据就是计量结果的记录；感悟小数和整数计数的共同之处，结合对是几的思考，建立起整数、分数与小数的关联，为揭示小数也是十进制数做好铺垫。

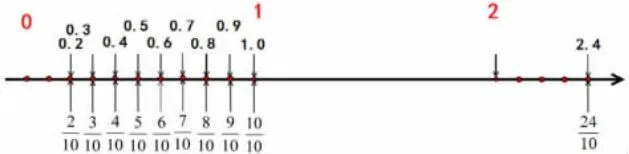
图4

三、迁移实践，抽象建构

小数初步认识到一定程度时，可以借助概念的正、负迁移，去伪存真，完善小数模型。

1.巧迁移：链式完善

教学中，布置任务：尝试找“我”的具体身高1.47 米（图5）。学生在充分讨论之后反馈，在数轴上标出了1.47，并尝试说明其意义。

图5

利用已经习得的一位小数的认知经验，创造性地理解1.47 米的意义，正迁移体会小数点后第二位上的数表示0.1 再十等分后计数的结果。（两位小数的意义虽不是本节课学习要求，但可以拓展）

还可以利用负迁移，辨析、厘清一些非本质属性，强化概念模型。由于前面学习的小数数量之间的进率都是10 或100，如0.8元=8 角，0.4 米=4 分米，部分学生容易形成错误的概括：零点几加大单位等于去掉零和小数点后的数加小单位。当遇到“0.5 时是多少时间”时，错误认知（0.5 时=5分）与默会认知（0.5 时是30 分钟）产生冲突，冲突引发争论。矛盾的解决需要学生联系所学的小数模型去解释，这样小数的意义更加明晰。

2.微主题：深度建构

本文中的“深度建构”指向两个方面：一是知识内部建立联结，即把小数和分数关联起来；二是数学和生活建立联结，用学到的数学知识去解决生活中的实际问题，提升学生学以致用的能力。

课后开展了微主题学习“制作身高尺”。

【情节回放】

（1）布置小组任务（见下表）。

?

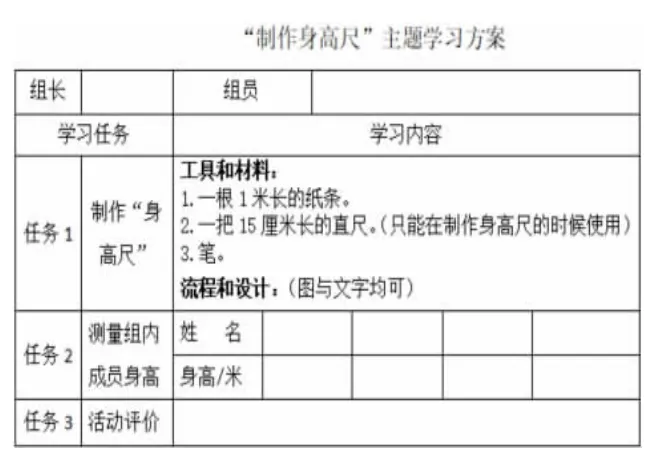
（2）学习成果及分享。

下面选取了部分小组的制作方案：

图6：为了方便读，我们组按每5 厘米记一个小数。大家都是1米多，记录身高时，小数点前是1米，小数点后的两位就是比1 米多的几厘米。

图6

图7：我们发现三年级学生身高大致在1.3 米到1.6 米之间，于是我们先找到纸条的0.3 米与0.6米，再在两个刻度之间用厘米进行细致刻画。

图7

图8：我们组都较矮，就将1米对折找到0.5 米，然后从1.5 米往下用厘米刻画了20 厘米即0.2米范围的刻度，刚好够量。

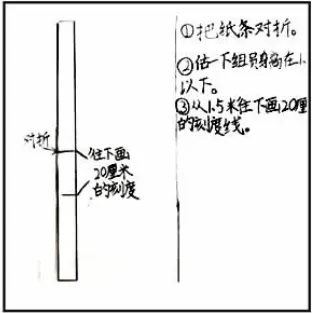
图8

从呈现结果来看，学生对小数都已有了较深刻的认识：不仅会在纸条上表征小数，也会以小数来计量身高，还会从量的角度进行大小比较，进行加减运算。

【课后反思】

小数的初步认识是小数意义学习的初始课，把重点放在小数应用的直观感受，小数意义的操作感知，以及概念模型的初步抽象上，可以优化教学、提升学生学习收获。

发挥学生在具体实物水平的认知基础，结合真实情境，理解小数不同数位的计量意义，展开合理的估计与判断，体会用小数刻画生活现象的简洁与精确。

在操作说明水平上做实做细，从实物模型到数学直观模型的演示，再到实践应用，梳理出小数和分数的关系，得出研究小数的方法。

基于丰富的小数表象，设计任务，进行正、负迁移，并在此基础上进行初步的抽象和概括，进阶数学思维，进而进行实践应用，发展数学素养。