问题导学：从探索规律走向模型建构——《多边形的内角和》教学设计与思考（二）

文|王守建

【教学内容】

苏教版四年级下册第96、97 页。

【教学过程】

一、基于学情，梳理问题

出示课题：多边形的内角和

师：同学们，看到课题，你有什么疑问？

生：什么是多边形的内角和？

生：怎么计算多边形的内角和？

生：多边形的内角和与三角形的内角和有关系吗？

生：怎样探究多边形的内角和？

……

【设计意图：“疑”是对知识的主动思考，是思维的助推器，能培养学生的创造力。“问”是对问题的主动描述，是探究的开始，是学习的重要目标。让学生看课题提出问题，一方面可以培养学生发现问题、提出问题的能力，另一方面，学生带着问题进入后面的探究活动，能让探究活动有方向、有深度、有趣味。】

二、唤醒经验，找到起点

师：（出示一组多边形）这些图形分别是什么图形？

生：三角形、四边形……

师：像这样，由三条及以上线段首尾相接围成的图形是多边形。谁能指一指多边形的内角？

师：我们已经探究了三角形的内角和是180°，请大家猜一猜，四边形、五边形……的内角和分别是多少？它们又与什么有关系？

生：长方形和正方形的内角和是360°，我猜四边形的内角和是360°。

生：五边形的内角和比四边形的内角和大，我猜五边形的内角和是480°

生：我猜多边形内角和的大小与边数有关系，多边形的边数越多，它的内角和就越大。

【设计意图：学生认识了部分多边形，知道长方形、正方形的四个角都是直角，知道了三角形的内角和是180°，这些都是学生的已有经验，有必要进行唤醒，让其真正成为学习的起点，之后的自主探究活动也会更加顺利且有效。】

三、问研相融，探究规律

1.始于简，单项探究

（1）自主探究

师：是不是我们猜的这样呢？你打算用什么方法验证？

生：用量角器量每一个角的度数，然后加起来。（板书：量）

生：把多边形的所有内角都剪下来，然后拼到一起。（板书：拼）

师：量和拼是我们探究三角形内角和时用到的方法，能不能精确算出其他多边形的内角和呢？

生：我认为用量角器测量的结果会有误差，多边形的角越多误差也会越大，测量比较麻烦。

生：我有一个问题，把所有内角剪下来拼到一起，如果大于360°怎么办？

生：三角形是边数最少的多边形，我们已经用量和拼的方法探究出三角形的内角和是180°，探究其他多边形的内角和，完全可以利用三角形的内角和来计算。

师：大家说得都很好，我们要学会用已知去探究未知。今天打算从哪一个多边形开始探究？

生：四边形，因为四边形只比三角形多一条边，相对简单。

师：是的，研究问题一般先从简单的开始，有序探究，然后发现规律再解决复杂的问题。请拿出《研究单（一）》，开始探究之旅。

【设计意图：“疑是思之始，学之端”。数学是思维的体操，学习中需要有质疑的声音，需要有思辨的发生。“能不能精确算出其他多边形的内角和呢？”营造质疑的时空，积极组织引导，让学生敢质疑、能质疑、善质疑。质疑声产生了有效共鸣，学生由此想到利用三角形的内角和探究其他多边形内角和的方法。《研究单》帮助学生开展探究活动，通过“想一想、分一分、说一说、算一算”的引导，使研究思路清晰，探究任务明确。】

（2）交流分享

生1：（如图1）A 点和C 点相连，正好把四边形分成两个三角形，两个三角形的内角和就是四边形的内角和。列式计算“180°×2=360°”。

图1

生：B 点和D 点相连也可以。

生2：（如图2）像这样可以把四边形分成三个三角形，列式“180°×3”，其中三个角不是原四边形的内角，它们的和是一个平角，所以“-180°”，最后结果是360°。

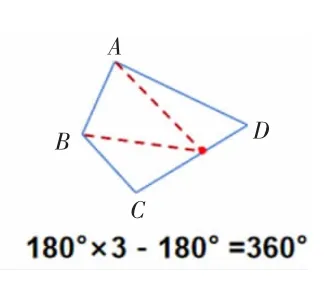
图2

生3：（如图3）在四边形内任意点一个点，四边形的四个顶点A、B、C、D 都和这个点相连，分成了四个三角形，这样就多出了一个周角，所以要减去360°。列式计算“180°×4-360°=360°”。

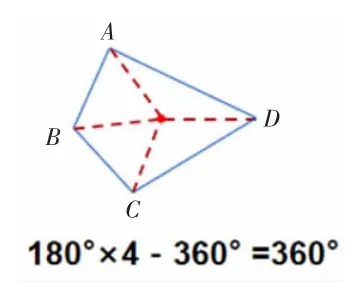
图3

师：观察比较这几种方法之间有什么相同和不同之处？

生：都是把四边形分成三角形，但分的三角形的个数不同。

生：第一种方法更简洁，后两种方法的计算，如果运用乘法分配律，其实都可以得到第一种方法的计算。

师：你的观察很细致，思考很深入，我们一起算算看。

【设计意图：把四边形分成几个三角形的方法一定不止一种，不论出现多少种情况，都要给学生交流分享的机会。引导学生围绕“这几种方法之间有什么相同和不同之处”进行观察、比较，不仅找到不同之处，还找到内在的联系，让思维向更深处发展。“一起算算看”，原来结果都是“180°×2”，对“有必要分成三个、四个三角形吗？”的思考水到渠成。】

2.趋于繁，整体探究

（1）自主探究

师：研究了四边形的内角和，能不能用这种方法接着研究呢？请大家拿出《研究单（二）》。

研究单（二）

研究内容：多边形内角和及其与边数的关系。

研究方法：分一分，算一算，想一想，说一说。

研究过程：

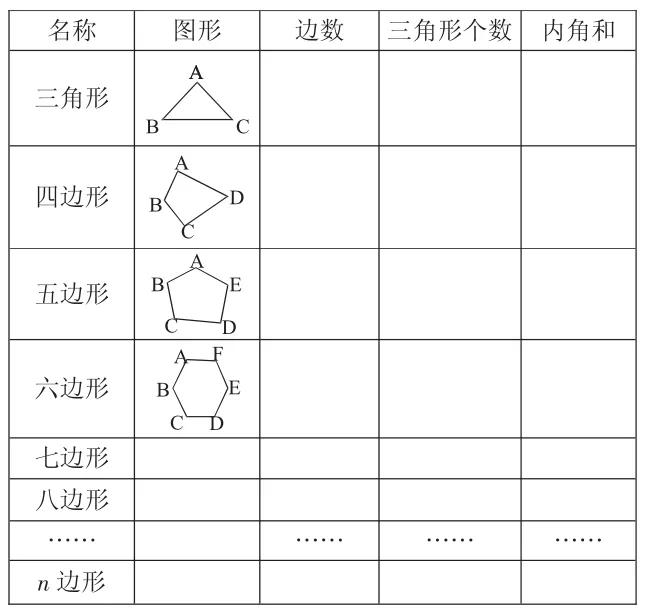
名称图形边数三角形个数 内角和三角形AA四边形BC A B C D A五边形B E CD A F六边形B E C D七边形八边形……………………n 边形

研究发现：_______________________________________

研究结果：多边形的内角和=________________________

【设计意图：有了探究四边形内角和的经验，这里放手让学生自己探究五边形、六边形等的内角和。《研究单》中，三角形、四边形、五边形、六边形都提供了图形，直观、具体，有利于学生的操作探究，能使学生充分感知多边形内角和的探究方法和探究思路。七边形、八边形、n 边形没有提供图形，内角和会是多少呢？既留给学生想象和个性化操作的空间，也倒逼学生因为需要而带着问题去寻找并发现规律。】

（2）交流分享

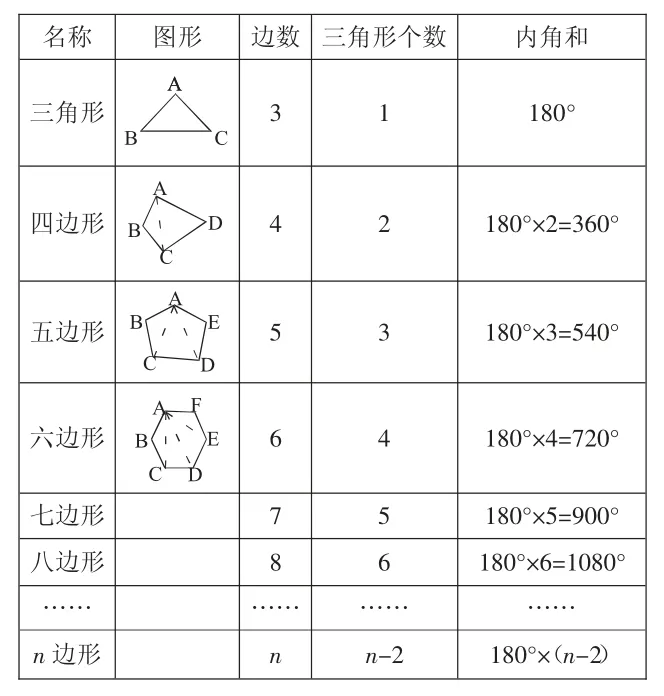
名称图形边数 三角形个数内角和AA三角形31180°BC A B C四边形42180°×2=360°D A B E 五边形53180°×3=540°CD A F六边形64180°×4=720°B E C D七边形75180°×5=900°八边形86180°×6=1080°……………………n 边形nn-2180°×（n-2）

生：（如上表）我在分三角形的时候都是从A 点开始，向与它不相邻的顶点连线。通过研究，我发现多边形的边数越多，分成的三角形的个数也越多，内角和越大，多边形的内角和等于180°乘多边形的边数与2 的差，如果是n边形，可以分成“n-2”个三角形，内角和是“180°×（n-2）”。

生：我也把六边形分成了四个三角形，分的方法略有不同。（如图4）

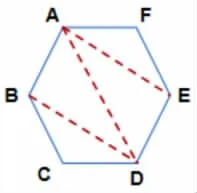
图4

生：我更喜欢第一种方法，从多边形的一个顶点出发，向与它不相邻的顶点连线，这样更有序。

师：这样有序有什么好处吗？

生：分出的三角形更好数。

生：不会多连，也不会少连。

生：我还发现了多边形每增加一条边，内角和就增加180°。

生：我发现竖着看，多边形的边数越多，内角和就越大；横着看，分成三角形的个数总是比多边形的边数少2。

师：你不仅善于发现，还善于总结。分成三角形的个数为什么总比多边形的边数少2 呢？

生：请大家看这些多边形，我们在分三角形的时候，从一个顶点出发，除了不与和它相邻的两个顶点相连，与其他每一个顶点都相连，所以分成三角形的个数总是比多边形的边数少2。

生：分成的三角形中，有两个三角形中的两条边是多边形的边，其余的三角形只有一条边是多边形的边，所以分成的三角形的个数总是比多边形的个数少2。

【设计意图：本环节的交流分享，着力点放在引导学生通过对有序排列的数据进行观察和比较，逐步抽象概括出多边形的内角和的一般计算方法，帮助学生进一步体会探究的意义和推理的价值。知其然，亦要知其所以然，“分成三角形的个数为什么总比多边形的边数少2？”引导学生继续思考，找到知识的本质。】

四、回顾反思，延伸探究

师：回顾刚刚的探究过程，你有什么收获或体会？

生：探究数学问题时，可以利用已学的知识把未知转化成已知。

生：探究问题要从简单的问题入手。要有序，还要多思考，注意发现并探究规律。

师：同学们不仅善于发现问题、提出问题，还能主动探究、深入思考，解决了问题，真了不起！那有没有新的问题要提出来呢？

生：能不能把多边形分成四边形来研究呢？

生：多边形有内角，有没有外角？如果有，它的外角和又是多少？

师：欢迎你们课后继续研究。

【设计意图：学生在探究活动中，既有收获，也有体会，通过回顾反思，再次给学生交流分享的机会。在回顾反思中，学会概括，学会表达。在问题引领下，学生解决了所提出的问题，在主题探究中，学生有可能发现或想到新的问题，给学生再次提出数学问题的机会，引导学生把课堂探究延伸到课外，丰富学生的学习活动。】

【课后思考】

一、在问题中探究

有意义的问题，是学生获得知识、探索规律的前提，也是学生解决问题、发展能力、提升素养的根本。课中，有教师提出的问题，也有学生自己的提问。教师不仅要善于向学生提问题，还要善于引导学生自己提出问题。将学习置于有意义的问题情境中，以学生为主体，积极组织学生以问题引领探究，问研相融，让探究更深入。

二、在探究中明理

数学是一门讲道理的学科，数学代表理性。在探究活动中，不仅要让学生知其然，还要使学生知其所以然。教学中，给学生充分探索、思考和交流的时间，让他们经历一个由模糊到清晰、由肤浅到深刻、由零散到系统的探究和发现过程。学生通过计算填表、观察、比较、分析、综合，归纳出多边形内角和的计算方法，学生通过呈现、介绍自己的《研究单》和探究思路，使隐含的道理明朗化。“多边形的内角和等于180°乘多边形的边数与2 的差，如果是n边形，可以分成n-2 个三角形，内角和是180°×（n-2）”，此时，没有让学生仅仅满足于发现规律的惊艳。“分成三角形的个数为什么总比多边形的边数少2 呢？”引导学生思考规律背后的原理，把握知识的本质，弄清知识的源与流。