感悟几何图形精髓 提升数学核心素养——“多边形的面积”练习的拓展与提升

文|彭伟铭

练习不仅要巩固基本的数学知识，更要注重渗透数学思想，应用数学方法，在深层次的探究过程中积累经验，提升能力。因此，多边形面积的练习设计不仅要有公式应用的基本题，还得有提升学生思维品质的拓展提高题，让学生进行深层次的思考，对图形的本质认识与应用有新的体会、发现与感悟。

一、发挥想象，让几何图形的公式“活”起来

大多数教师和学生在一堂课的探究推导得出图形的面积公式后，都会觉得大功告成，接下来就是公式的熟练应用了。几轮巩固的习题做下来，公式套用是熟练了，但公式同样也被学“死”了。教学中可以由公式逆推回图形，或是应用公式时，改变某些条件，使公式“活”起来。

1.从公式逆推回图形

从图形推导出公式，是一个从直观到抽象的过程，在学生对转化方法应用较为熟练时，可以引导学生从抽象到直观，也就是从公式逆推回图形。比如三角形面积的推导（图1），不同的推导方法，会使公式的书写顺序有所改变。

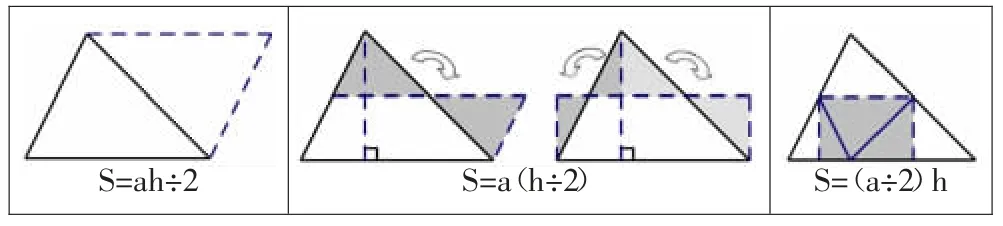
图1 三角形面积推导

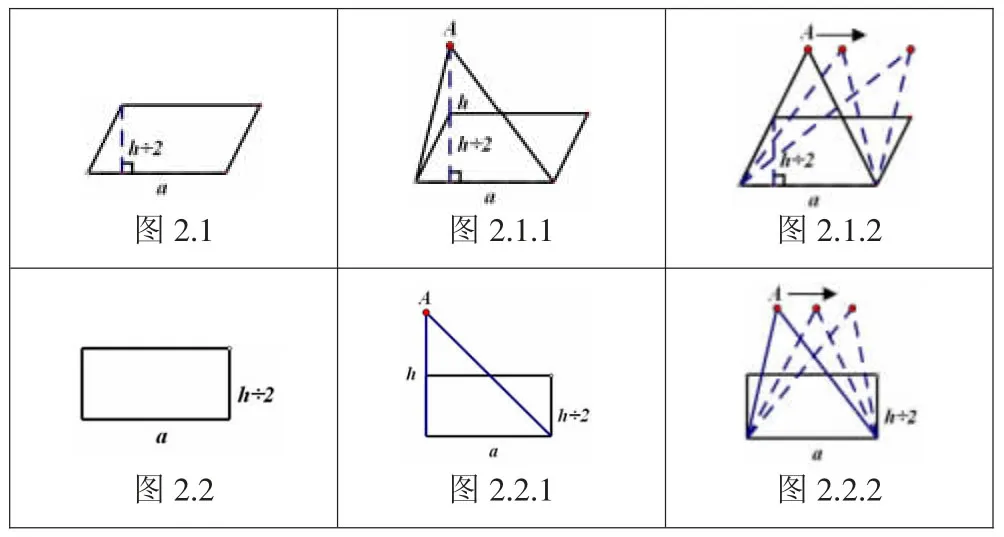
图2 公式逆推回图形

根据公式的不同写法，设计了这样一道练习：

你能根据三角形面积公式的三种不同写法，分别画出三角形吗？

①S=ah÷2 ②S=a（h÷2） ③S=（a÷2）h

对于①，引导学生：看到ah,你会想到哪个图形？（平行四边形）“再除以2 呢？这图形有什么变化？”让学生试着根据公式画一画。

对于②，引导学生把h÷2 看成一个整体，你会想到什么图形？学生能想到长方形或平行四边形，画出如图2.1、图2.2。由图可知，和它们面积相等的三角形的高肯定是长方形或平行四边形高的2 倍（图2.1.1和图2.2.1）。水平移动A 点，这样的三角形能画出很多（图2.1.2和图2.2.2）。

教师水平移动点A 进行动态演示，一是可以帮助学生理解同面积同底的三角形与平行四边形或长方形间的关系。二是可以让学生回顾用割补法推导三角形面积的过程（图3）。教师可以趁此动态演示水平移动线段AB，三角形转化成平行四边形时割补法的多种应用方法，学生感慨：原来还可以这样割补啊，以前怎么没想到呢！

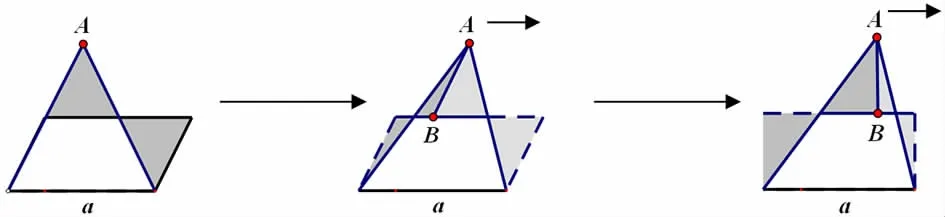
图3

在图形与公式、公式与图形的相互转换中，学生对转化思想、转化方法的掌握与应用更熟练了，对知识点的把握与理解也更深刻了，对图形几何变换的意识和能力也提高了。以后碰到变换的或更复杂的几何问题时，学生也就更容易找到解决问题的方法。

二、巧妙设计，让几何图形的本质“凸”起来

图形变式中渗透转化思想。

1.非标准图形转化为标准图形

平时学生的练习大多是求标准图形的面积，这类练习做多了，学生一旦碰到变式的图形，就会出现一系列的问题，或是不会找高，或是找错了对应的底和高，又或是分辨不出上下底。对待这类只变动了位置的图形，最简单的方法就是旋转图形，把图形变回到标准图形，再去找底和对应的高。

2.繁琐图形转化为简单图形

一块梯形的草地，中间有一条宽为2m 的小路，求草地的面积（图4）。这题学生最常想到的方法是用梯形面积减去长方形面积。如果学生的几何变换能力较强的话，他会在脑海中对两块草地面积进行拼合，拼合成一个上下底各缩短2m、高不变的新梯形。这道题可能体会不出图形变换后更简便的好处，那我们接着下一题：一块长16m、宽10m 的长方形草地，中间有两条宽为2m 的路，一条是平行四边形，一条是长方形，求草地的面积（图5）。同样的，学生的第一个念头是“挖”，从长方形的面积里分别挖去两条小路的面积。这种方法很容易错在两条路重复的面积减去了两次，却忘了还得加回去一次；或是先从一条小路中去掉重复的面积，再加上另一条路的面积。如果换一个角度，四块草地的面积不能直接求，那看看能不能拼合，在脑海中进行移动拼合，形成的刚好是长和宽减少了2m 的新长方形。这样把较繁琐的图转化为简单的图形，就能很快地找到解决方法。

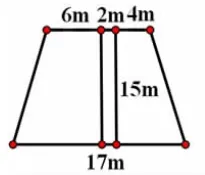
图4

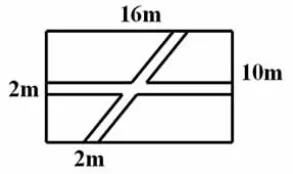
图5

我们还可以更进一步：一块长10m、宽8m 的长方形草地，中间有三条宽为2m 的平行四边形的路，求草地的面积（图6）。

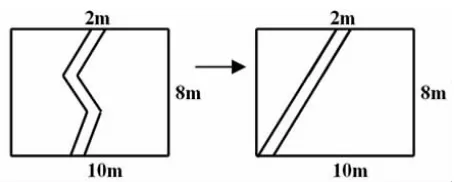
图6

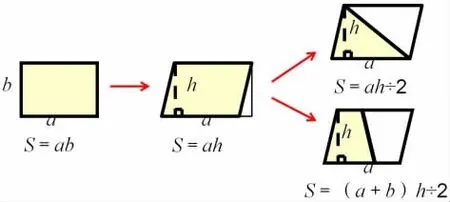
图7 多边形转化图

有了前面的图形转化的经验累积，学生很快就能想到转化方法。

方法1：把两块不规则的草地面积移动拼合成一个长缩短2m、宽不变的新长方形。

方法2：把三条小路进行旋转拼合，发现不管中间有几条平行四边形的路，也不管每条平行四边形路的高是多少，它们都能转化为一个大的新平行四边形，再用长方形的面积减去新平行四边形的面积，一下子就把复杂的问题简单化了。

3.不规则图形转化为规则图形

为了计算不规则图形的面积，常常需要变动图形的位置或对图形进行分割、旋转、拼补，使它变成可计算出面积的规则图形。

平时的练习设置中，应让学生通过转化凸显出几何图形的本质，培养学生的转化意识，增强学生对图形的切拼构造能力及图形的对称、旋转和平移的几何变换能力。

三、沟通联系，让几何图形的形态“动”起来

1.沟通图形面积间的联系

在整理复习课中，通过让学生回忆各个图形面积的推导过程，体会到图形之间是可以互相转化的。在教学中进行这样的动态演示（图8），梯形的上底慢慢缩短变成三角形，梯形的上底慢慢延长变成平行四边形，让学生观察图形的变化与公式的变化，体会几何图形间的本质联系。还可以加入长方形和正方形这两种已学图形，沟通它们与平行四边形的联系与区别（如图9）。

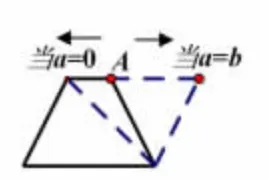
图8 移动点A

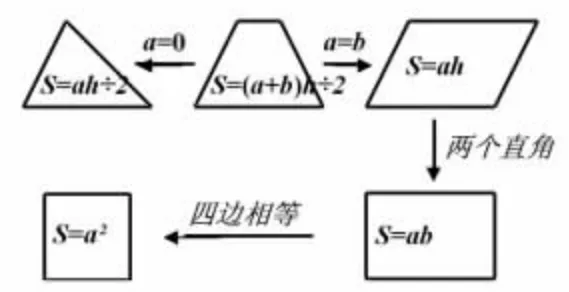
图9 多边形的联系

2.沟通图形变式间的联系

在练习时，让图形上的某个点或某条线段动起来，让学生观察对比，感受图形本质，是一个不错的方法。如图10，水平移动A 点，形成了不同的三角形，通过观察这些三角形，发现这些三角形的共同点：同底等高的三角形面积相等，并提问，像这样的三角形你还能找到吗？

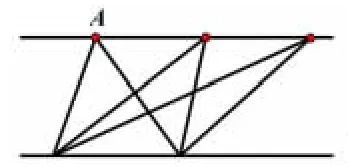
图10 移动点A

如果把这个三角形放到平行四边形中，就会有新的变化。如图11，空白部分的面积与阴影部分面积有什么关系？学生最先采取的方法是分割法。如图11 的方法1，添辅助线，把空白三角形分成两部分，分别与阴影各部分的面积相等，从而阴影面积与空白面积也相等；或是用字母a、b 表示两个阴影三角形的底，并进行代数推导。教师引导学生用“同底等高的三角形面积相等”的知识点对阴影部分进行转化，如图11 的方法2，把两块阴影部分的面积转化成大三角形的面积，发现刚好是平行四边形的一半，所以阴影面积与空白面积相等。还可以沿着平行四边形的边移动A 点，感受变动的三角形与平行四边形间的联系，如图12。

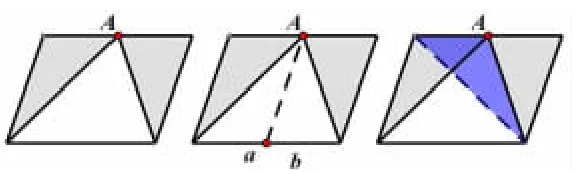
图11

图12

通过动态演示，让学生明白：虽然A 点在移动，三角形在变化，但它们都可以通过“等底等高的三角形面积相等”的规律等积转化成上图的第一个图形。

我们还可以更进一步，当A 移动到平行四边形内时，它们的关系又会发生什么变化？如图13。当然我们可以用分割法或代数推导法，也可等积转化成上面我们讲过的图12。学生会发现不管图形怎么变，总有些性质是不变的，抓住图形间的联系，我们总可以把不熟悉的图形转化为熟悉的图形。学生经历并思考了图形的动态变化过程，对转化的理解会更深刻，碰到图形变式时，更容易透过现象发现本质。

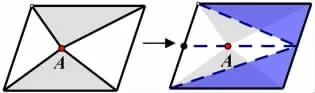
图13

综上所述，在设计几何图形综合发展练习时，应力求图形的活、变、动，充分深入挖掘图形，让学生在深层次的思维练习中感受数学的趣味性，并乐于思考、勇于探索，培养学生发展性、创造性的数学思维品质。