适时追问，培养学生思维

刘瑞文

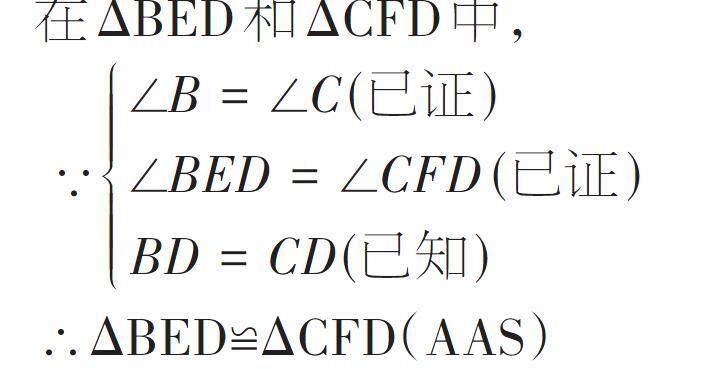
摘要：近日，教育部发布了2022年版义务教育课程方案和课程标准修订情况。新课标聚焦发展学生的核心素养，对重大主题教育进行了整体规划和系统安排。让核心素养落地，是本次课程标准修订的工作重点。

关键词：课堂教学  核心素养  思维培养

学生的素养发展，贯穿新课标全文本，隐含在课程内容及教学实践中，体现在课程学习结果的具体描述中。例如，数学学科提出应培养学生具有如下素养：会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界，简称为“三会”。

如何在自己的课堂中将落实核心素养与课堂基本知识传授相结合，是每个数学教师应该深度思考的问题。数学课一直给人的印象就是抽象难懂，枯燥乏味的，尽管现在很多农村学校都安装了电子白板，借助多媒体进行教学后，我们的数学课堂变得更直观了，更有活力。对于初中学生而言，我觉得第一“会”不难做到，难的是后面“两会”，所以教师在平时的教学中要有意识地引导学生朝这两方面来发展。

结合平时教学中的经历，我发现在课堂中有效的追问能提高学生的学习能力，能够让学生在发生错误时迷途知返，能够在学生理解重难点处画龙点睛。追问运用得当，对于学生明确自己的想法，提高学生思维活动的完整性和准确度有很大帮助。以下是我在教学中对追问的一些实践与探索。

一、在意外之处追问

叶澜老师说：“课堂应是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的风景，而不是一切都必须遵循固定的路线而没有激情的旅程。”如下试题：

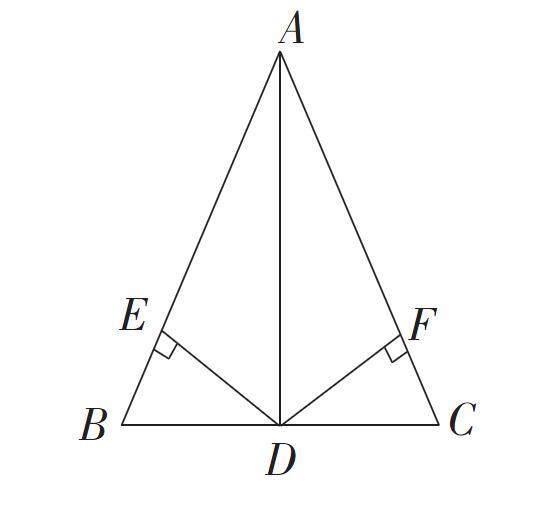
在ΔABC中，AB=AC ， BD=DC，DE⊥AB，DF⊥AC，那么DE与DF相等吗？说明理由。

本来我是预设学生利用刚学到的三角形全等的条件 来证明的，让学生思考片刻后，我请一位学生上台写出他的证明过程：

解：∵AB=AC ，BD=DC

∴∠BAD=∠CAD

∵DE⊥AB，DF⊥AC

∴DE=DF

这位学生的证明出乎我的意料，因为他用的是我还没有讲到的知识来证明的，所以我非常高兴地表扬了这位学生超前学习的能力，然后我在这位学生的每个解题步骤后面都加上一个括号，变成了以下这样：

解：∵AB=AC ，BD=DC（     ）

∴∠BAD=∠CAD（            ）

∵DE⊥AB，DF⊥AC（         ）

∴DE=DF（                 ）

让他把每一步的依据也备注在括号里，了让其他的学生感受一下他的解题思路。接着继续发问：“有谁用其它方法证明的吗？”我从举手的部分学生里又叫了一位学生上来解题，具体步骤如下：

解：∵AB=AC （已知）

∴∠B=∠C（等腰三角形两底角相等）

∵DE⊥AB，DF⊥AC（已知）

∴∠BED=∠CFD（垂直的定义）

在ΔBED和ΔCFD中，

∵[∠B=∠C（已证）∠BED=∠CFD （已证）BD=CD（已知）]

∴ΔBED≌ΔCFD（AAS）

这样一来，既让台下的学生体会到两种思维方式的特点，也为他们后面的学习做了一下热身，可谓一举两得。

课堂教学随时会有出乎教师意料之外的情况发生，如果教师总是按照自己的教学计划来组织教学环节，就会无形中束缚了学生们的发散性思维，不利于培养学生的创新思维。因此我们对于学生的“意外表现”，要积极回应和主动追问，激活学生思维，拓展想象空间，让教学中的“节外生枝 ”演绎出独特的价值。

二、在出现错误之处追问

学生在课堂中出现一些差错是不足为奇的，当我们遇到这种情况时不应以一个“错”字责备学生，更不要直接说出正确答案，而应该正确解读学生的错误，弄清楚产生错误的原因，再把握合理的纠错时机，通过追问的语气和角度来引导学生片面的解读，让学生自己意识到错误并且纠正。

例如，在讲到“相遇问题”时，进行如下试题时：

甲乙两地相距720千米，两车同时从甲乙两地相向开出，甲车速度是100Km/h，乙车速度是80Km/h，求几小时后两车相遇？

学生在求解过程出现了两种列式：

（1）720÷（100+80）

（2）720÷100+720÷80

针对这两种情况，我没有说明谁对谁错，追问学生：“你们觉得哪种列式才是对的呢？同意第一种解法的举一下手，认同第二种解法的举一下手。”结果有一部分学生没举手，“那些没举手的学生是认为两种都对还是有不同看法？”然后让没举手的那部分学生把两种解法的答案求出来。当他们发现得数不同时，我继续追问：“得数怎么会不一样呢？是不是算错了？”学生通过验算发现计算没错，那问题出在哪里呢？我又从认同第二种解法的学生中选出一名代表，“给大家说一下你这样列式的思路吧。”学生说：“因为利用分配律，720÷（100+80）可以转化为720÷100+720÷80， 所以我就列出这个式子了。”听到“分配律”一词，我就知道知道学生出错的原因了，顺着这个“症结”，我继续发问：“请大家回忆一下，你们学过的分配律是在哪种运算当中出现的？”“乘法分配律。”学生异口同声回答。“有没有除法分配律？”“没有。”

如果教师一开始就对“720÷100+720÷80”这种算式“一错而过”，置之不理，就不会出现“百家争鸣”的场面。因此，在学生的错误之处适时地追问，可以让学生有更多的机会阐述自己的想法，让学生领着学生们去探究错误产生的原因，比起教师直接向学生解释正确答案，效果真是好太多了。

三、在缺乏深度之处追问

七年级学生在学习过程中，很多时候对问题的思考都只是停留 在片面，这时教师要有意识地追问和引导，搭设思维跳板，帮助学生开拓思路。

例如，在讲到“相交线和平行线”的内容时，设计如下试题：

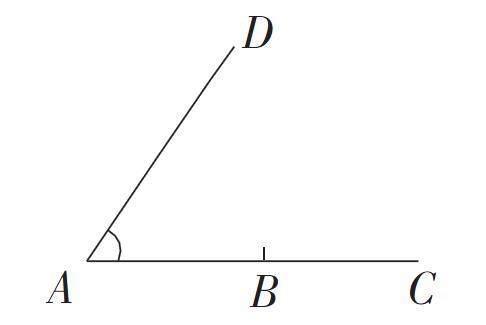
如图，以点B为顶点，射线BC 为一边，利用尺规作∠EBC，使得∠EBC=∠A，EB与AD一定平行吗？

在讲解这道题之前，我让学生们先在课本上作图，在巡视过程中发现多数学生只画出了一种情况，于是我叫了一位学生上黑板来画，他的图是这样的：

我首先肯定了这位学生的做法，并问：“如何判定AD//BE呢？”“因为∠DAB等于∠EBC，根据同位角相等，两直线平行可以得到AD//BE。”学生回答。

我又问：“请大家仔细观察一下原图，以B点为顶点，以射线BC为一边的角只有一个吗？”过了一会儿，有人回答：“可以把BE边画在BC边下方！”一石激起千层浪，台下的学生恍然大悟，纷纷画出了第二种情况的图形：

从第二个图形可以很直观地看出，AD不会跟BE平行。因此，在学生思考欠缺深度时，通过一环扣一环的追问，引导学生将问题一层层剥开，使其知其然，又能知其所以然。这对于引发学生自主探究，提高学生思维的敏捷性和深刻性，构建完整的知识体系具有关键的作用。

在实际教学中，促进学生核心素养的方式有很多，不同的老师有不同的方法，但“追问”应该是每位教师在每一节课上都能用到的，课堂中的追问是教师教学智慧和教学艺术的体现，是促进学习氛围的催化剂。适时的追问开启了学生思维的阀门，可以为学生在自主探究活动中“跑偏了”的时候拉一把，既提升了教学质量，又演绎了课堂的精彩。

总之，课堂是学校教育中核心素养能否真正落地的关键环节，教师们首先要用核心素养更新自己的教育理念，才能提高教育教学质量，进而促进学生核心素养的发展。