培养模型观念的初中函数教学实践

缪娟

摘 要：初中阶段培养模型观念，需要借助具体的教学内容，如“数与代数”中的方程、不等式、函数，“图形与几何”等.针对“用一次函数解决实际问题”一课进行教学实践，既关注数学与实际的结合，让学生体会一次函数是刻画现实世界数量关系的有效数学模型，加深对模型观念的认识与理解，又让学生借助函数图象分析问题，形成解决问题的思路，发展模型观念，会用数学语言表达现实世界.

关键词：模型观念；一次函数；函数图象

《义务教育数学课程标准（2022年版》）明确指出函数的教学目标：能用适当的函数表示法刻画简单实际问题中变量之间的关系，理解函数值的意义；能确定简单实际问题中函数自变量的取值范围，并会求函数值；能结合函数图象对简单实际问题中的函数关系进行分析.由此可见，实现目标的关键能力是：“关注数学知识与实际的结合，让学生在实际背景中理解数量关系和变化规律，经历从实际问题中建立数学模型、求解模型、验证反思的过程，形成建模观念.”模型观念作为初中阶段的核心素养之一，应在平时教学实践中积极尝试，促其落地生根.

1 教学价值

“用一次函数解决实际问题”是初中数学（苏科版）首次运用函数知识解决实际问题的标志性内容，围绕学生进入初中后“用图象解决问题”的难点，笔者针对这一难点，以行程问题为载体进行一次函数应用专题复习教学实践，期望帮助学生打开突破口，培养模型观念和应用意识，并且一次函数应用题是历年来南京中考的常考题型，它常把应用题与一次函数融合在一起，又高于应用题，它需要学生具备一定的综合能力.

2 问题思考

结合学生在解决与实际生活密切联系的一次函数应用题时，可发现其主要的困惑有：（1） 不知道先去想象实际情境，不能还原实际情景，导致不知道题目说的是什么意思；（2） 不知道从图象上何处获取信息，怎样获取信息；（3） 习惯用算术或方程方法，不知道建立函数模型解决问题，所以对于过程比较复杂，量的变化比较多的题目，无法理顺这些量之间的关系.然而解决这类问题往往需要通过读图识图、借助数形结合来帮助学生分析、解决问题.鉴于此，教学实践分为从以下三个活动进行.

3 教学实施

3.1 基于理解，紧扣变量，看图说话

问题1：请你把这个故事说完整.

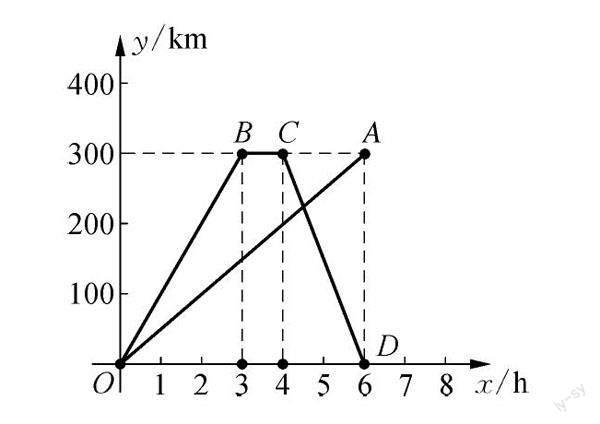
图中的线段OA和折线OBCD分别表示一列慢车和一列快车沿直线从甲地开往乙地……

学生1：在一条直线上有甲、乙两地，一列快车和一列慢车从甲地同时出发开往乙地，慢车以50km/h的速度匀速行驶了6小时到达，快车以100km/h的速度匀速行驶共3小时到达乙地后停留了1小时，再以150km/h的速度匀速行驶2小时返回，慢车到达乙地时快车正好返回到甲地.

教师追问：要想把这个故事说完整，你是如何分析函数图象，从图中获取信息的？

教学说明：引导学生根据图象把故事說完整再进行追问，师生交流得到从图象获取信息的关键是基于对函数图象的三个理解：首先要理解变量x、y的实际意义；再理解特殊点的实际意义即根据特殊点的坐标明确每段路径中的时间、速度等相关信息；最后理解点与点之间的关系即实际情景每段具体的行驶路径.“看图说故事”活动的设置是将实际生活情境与图象进行对接，让学生学会阅读图象.

3.2 依据经验，借助手段，转化信息

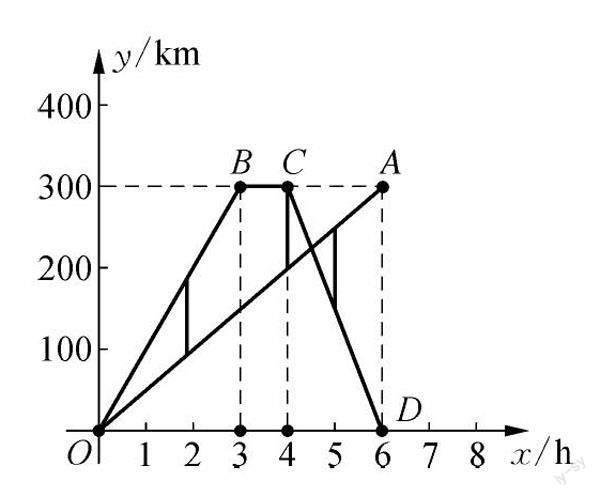
问题2：请画出一些关键时刻两车行驶的线段示意图.

快车、慢车相遇时线段图

教师追问：选择的时刻和图象中哪个点是对应的？为什么？

学生2：因为变量y表示两车距离甲地的距离，所以当两车距离甲地的路程相等时，即两车相遇.

教学说明：根据以往的学习经验，对于行程问题可以借助线段示意图帮助理解两车之间的行驶路径，把函数图象上某一特殊时刻的实际情景用线段图来表示，从而把图象信息向实际情景进行转化，进而深刻理解题意，帮助学生强化综合与分析的能力.

3.3 聚焦探索，注重提炼，应用信息

问题3：请提出一些问题并解决.

学生3：求出各段的函数表达式？

慢车：yOA＝50x（0≤x≤6）.

快车：yOB＝100x（0≤x≤3），

yBC＝300（3＜x≤4），

yCD＝300-150（x-4）（4＜x≤6）.

教学说明：学生利用已知点的坐标，运用待定系数法或数量关系法都可以求出每段图象的函数表达式及其它各点坐标，求出相关图象的函数关系式，后面可以利用函数关系式解决实际问题.

学生4：两车何时相遇？

当yCD＝yOA时，列得方程50x＝300-150（x-4），解得x＝4.5，即两车在出发4.5小时后相遇；

教学说明：求两车相遇的时间就是求图象上点P的横坐标.

学生5：两车何时相距50、100、150km等等？

以相距100km为例：

当0≤x≤3时，列得100x-50x＝100，解得x＝2；

当3＜x≤4时，列得300-50x＝100，解得x＝4；

当4＜x≤6时，列得50x-［300-150（x-4）］＝100，解得x＝5.

教师追问1：“两车之间的距离”能在图象上表示出来吗？

教师追问2：这些问题如何变成一个问题？能不能从函数的角度研究这个问题？

教学说明：“两车之间的距离”就是在横坐标相同时，图象上的点的纵坐标的差，只要把两车的函数关系式相减，即可表示出两车之间的距离.利用函数模型解决问题就是将实际问题转移到图象上，把问题中涉及的量转化为图象上点的坐标，再利用函数关系式可以快速求得结果，既直观又简便.

学生6：两车之间的距离s（km）随x的变化而变化，s（km）是x（h）的函数.

教师追问3：如何画出s（km）与x（h）函数图象？

教学说明：s（km）与x（h）之间的函数是两个一次函数的差，所以整个过程s（km）与x（h）之间的函数仍然是一次函数通过对图1的分析可知图象分为四段，确定出每一段与每一段之间的拐点的时间与距离，第一段（OB段）：两车从甲地同时出发，图象看出两车之间的距离在不断增大，直到快车到达乙地，此时两车之间的距离为150km对应的时间是0≤x≤3；第二段（BC段）：快车到达乙地后停留了1小时，两车之间的距离在慢慢变小，直到快车返回甲地，对应的时间是3＜x≤4；第三段（CP段）：两车相向而行，直到相遇，这时s＝0km，对应的时间是4＜x≤4.5；第四段（PD段）：两车相遇后继续行驶，快车到达甲地同一时刻慢车到达乙地，这时两车相距300km，对应的时间是4.5＜x≤6根据以上信息可描出相应的点，就可以画出图象.

4 对培养模型观念的函数教学思考

4.1 整体教学是模型观念培养的重要教学方式

《课标（2022年版）》要求数学教学要重视围绕单元进行整体教学设计，既要体现各学科知识之间内在的逻辑关系，又要关注数学知识点与核心素养之间的外在关联.本节课例是一次函数的应用，教师需要引导学生站在整个“一次函数”单元乃至“函数”大单元的高度，合理建构一次函数模型，运用一次函数的图象与性质解决实际问题，加深学生对一次函数的理解与认识.学生在本章的学习和研究中，已经掌握了一些应用数学模型解决现实问题和建构数学模型的基本路径，本节课的教学重难点是借助函数图象解决较为复杂的现实问题，帮助学生进一步加深和巩固数学模型的意识和能力.案例中学生4和学生5提出的问题都是可以用方程模型来解决的，甚至还有学生运用算术方法，但在教师的追问下，引导学生深入思考和体会“两车之间的距离s（km）随x（h）的变化而变化，s是x的函数.”这样，教师逐步引导学生站在模型观念的高度，结合已有经验，运用不同模型解决问题，最终回归函数模型.

4.2 “自”构情境，注重数学化过程，发展模型观念

发展模型观念需要选择好的载体，而好的载体依托好的情景，教师可让学生自主搭建情景，使其更贴近学生的最近发展区.问题1要求学生自主设计问题情景，目的是逆向为学生提供模型建构过程.活动过程中每一个同学都有话可说，让学生的思维在与同伴的对话和老师的交流中涌出来.这一过程是用函数解决问题的逆向思考，培养学生的发散思维，进而加深对数学模型的理解，积累建模经验，从而实现教学不仅能从条件推演结果，也可以从结果想象条件，这是数学建模的重要方法.

4.3 自主探究，提升“四能”，发展模型观念

模型建构的过程离不开学生的问题意识，教师设置自主探索活动，由学生自己提出不同思维层次的问题.比如学生3的问题突出基础，利用已知点的坐标和待定系数法或数量关系法，求出每段的函数表达式及其他各点坐标；學生4、5和6三位同学能够将实际情境与图象结合，挖掘图象信息，提出了行程函数问题与方程、不等式的密切联系的问题；最后教师引导学生体会用函数的观念解决问题，利用图象直观看出两人相距问题，其实就是在横坐标相同时，图象上的两点的纵坐标之差，利用函数关系式运算即可得到结果.模型的建构需要学生先发现问题和提出问题，还需要教师适当引导或让学生经历猜想讨论等活动.在进一步培养模型观念的过程中，“四能”所涉及的能力自然得到提升，且提升效率较高.

4.4 渗透数学思想方法，发展模型观念

近年来，中考对函数的考查开始回归自然、回归函数的本质，重视对函数建模思想和函数对称性、增减性及最值等主要性质实际应用的考查，较好地体现了“问题情境—建立模型—解释、应用与拓展”这一知识形成与应用过程，对一线教师起到了正确的导向作用.在教学中引导学生自主建构模型、准确理解模型、熟练应用模型，既有利于学生深刻认识相关内容的核心，还能少走弯路，减少负担.函数模型思想和数形结合思想的重要性无须再多赘言，我们要将数学思想在此题及拓展变式问题的解决过程中.

参考文献：

［1］ 兰育哲.回顾促思 层层推进——“长方体和正方体”单元复习的思考［J］.数学之友，2022，36（5）：52-53.

［2］ 徐翠萍，孔德宏.2021年全国高考数学甲卷理科第21题的解法及变式探究［J］.数学之友，2022，36（4）：87-89.

［3］ 蔡陈.严谨检验，灵活解题——由函数的奇偶性错解分析引发的思考［J］.数学之友，2022，36（4）：67-69.

［4］ 郑建庆.“核心素养”视域下提升教学设计能力的实践研究——以《椭圆的定义与标准方程》教学设计为例［J］.数学之友，2022，36（4）：36-37.

［5］ 罗理想.高考数学解析几何考查状况分析——以2021年高考数学全国二卷为例［J］.数学之友，2022，36（3）：81-82.

［5］ 陈万寿.从三个事件互相独立的条件谈起［J］.数学之友，2022，36（3）：55-56.

［6］ 马洪超.打造“极简理念”下的生态数学课堂——以《函数与方程》一课为例［J］.数学之友，2022，36（3）：32-33.

［7］ 樊欣，马小琼，韦华益，唐剑岚.动感技术的融合提质增效数学教学——以“反比例函数图象与性质”教学片段为例［J］.数学之友，2022，36（2）：88-89.

［8］ 马进.高中数学核心素养培育视域下的项目式学习研究［J］.数学之友，2022，36（2）：73-75.

［9］ 周晓丰.指向素养达成的数学作业设计思考［J］.数学之友，2022，36（1）：40-43.

基金项目：江苏省教育科学“十四五”规划2021年度重点课题《基于“四能”的初中数学模型建构的案例研究》（批准号：B/2021/02/170）.