传统学具在第二学段数学课堂中的创意应用

谭彩琴

摘要：根据小学生的认知发展规律，在第一学段的数学课堂中，小棒、圆片、小方块、钉子板等传统学具经常出现，而第二学段课堂往往难寻踪迹。然而，实践表明，第二学段数学课堂创意使用传统学具，能起到画龙点睛的作用，其能够帮助学生厘清算理，建立空间观念，体会基本的数学思想，将思维引向深处。

关键词：传统学具;高年级;算理;数学思想;深度学习

传统学具是小学生数学学习不可或缺的工具，对他们的数学学习具有积极影响。传统学具种类繁多，常用的有小棒、圆片、小方块、钉子板等。根据学生的认知特点，在第一学段数学课堂中，教师经常设计一些操作活动，让学生借助数学学具的操作应用，激发学习兴趣，使抽象的数学概念形象化，帮助他们理解数学概念。

在第二学段数学课堂中，教师往往过高地估计了学生的抽象能力，课堂上学习内容的增加也导致教师放弃学生动手操作的时间，导致传统学具难寻踪迹，取而代之的是多媒体信息技术的使用。然而，研究表明，第二学段的学生仍处在具体运算阶段，他们还需要具体事物的支撑才能形成简单的抽象思维。在实际授课过程中，我们也发现，第二学段数学课堂创意使用传统学具，能起到画龙点睛的作用。利用操作的直观感受，能够让高年级学生在操作中建立数学模型，将数学概念、数学方法、数学思想和具体的实物联系起来，从而加深对数学知识的理解，让学生从本质上把握数学知识。

下面，笔者从三个方面来谈一谈传统学具在第二学段数学课堂中的创意应用。

1    运用传统学具，帮助学生理解算理

数学是一门讲道理的学科。学生在学习的过程中不但要获得数学方法，还要理解方法背后蕴藏的数学道理，“知其然更知其所以然”。然而，抽象的数学道理往往难以让小学生接受。而传统学具恰恰可以将抽象的道理形象化，它给学生提供了可触摸的、具体的实物，将抽象的道理用直观的方式表达出来，让学生豁然开朗。

例如，学生在学习了2、5的倍数特征之后，紧接着学习3的倍数特征。可是3的倍数特征与2和5的不同，需要将各个数位上的数字相加，看是不是3的倍数。对于这一结论，教材上也只是让学生依样画葫芦，计算各个数位上的数字之和。爱动脑筋的学生会产生疑惑：为什么要把各个数位上的数字相加呢？教师也总是搪塞而过。如果在这个时候，教师能够引导学生将传统学具中的计数器和小棒配合使用，问题就会迎刃而解。我们先从一位数说起，3的倍数就是除以3没有余数。个位上的数，三个三个地分，没有剩余，那么这个数就是3的倍数。如果这是一个两位数，我们在计数器十位上拨一颗珠子，就表示1个十，换作10根小棒来三三分之，就会剩1根;十位上两颗珠子，表示20，三三分之，剩余2个1根，以此类推，十位上是几，那么三三分之，就会剩余几个1。再看百位，如果计数器上百位是1，那么用100根小棒，三三分之，剩余1;有几个百就会剩余几。这样，最终就将每一位上剩余的小棒合起来，三三分之，就能判斷是否是3的倍数了。而每个数位上剩余的小棒数恰好就是那个数位上的数字。如图1，234中有2个百，三个三个分，剩2;3个10，三个三个分，剩3;个位4暂且不分。剩下2+3+4=9，用9再继续三个三个分，正好分完，说明234就是3的倍数。如果最后分不完，比如235，最后剩2+3+5=10，10÷3=3……1，说明235就不是3的倍数。学生在操作的过程中，能够很好地感悟、理解这个规律背后的道理。有了这样的操作经验，还可以引导学生自己利用学具尝试解决9 的倍数特征：每一位的数字之和是9的倍数，这个数就是9的倍数。学生实现了对问题本质的理解，进行深度学习，并将其正迁移，拓宽了自己的视野。

再如，教师采用不完全归纳法让学生在举例、猜想、验证过程中逐步获得结论。而对于为什么奇数+奇数=偶数这样的现象并没有过多解释。其实，如果在这个时候，能够让学生自己摆一摆小圆片，就能将感性认识上升到理性认识。奇数就是单数，两个两个圆片组合，最后剩余1个（如图2）。第一个奇数剩余1个，第二个奇数也剩余1个，剩下的两个正好又配成1组，没有剩余，所以和就是偶数。同样的道理，学生通过操作，还可以深度理解偶数+偶数=偶数，奇数+偶数=奇数的深层次原因。这样的直观体验和学生将来数学学习中的逻辑证明仅有一步之遥，让学生真正从理性上理解这个规律。

2    运用传统学具，培养学生的空间观念

在图形与几何领域的学习中，空间观念是学生空间想象能力的基础，培养学生的空间观念是小学数学重要的教学目标之一。在学习中，借助传统学具的操作可以帮助学生获得大量的感性认识，锻炼学生的动手能力。在手脑配合的过程中，鼓励学生进行积极思考，学生的学习兴趣会随之增强。学具的直观性能够帮助他们较好地建立空间观念，从而理解图形的特征、图形的运动，发展学生的空间想象能力。

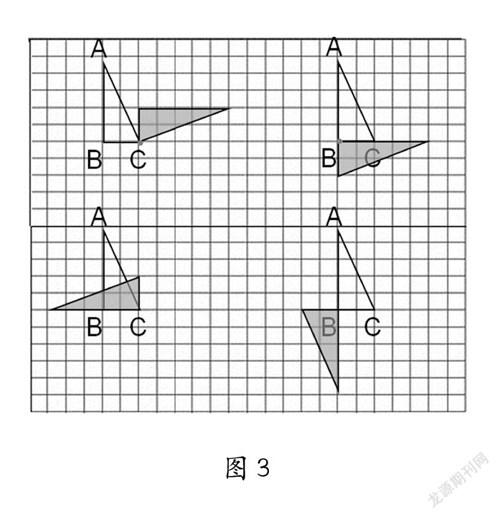
在“图形的旋转”一课学习中，旋转有三要素：旋转中心、旋转方向、旋转角度，学生在理解上总是存在一定的困难。比如：直角三角形ABC绕不同的点沿不同的方向可以旋转出不一样的图形，部分学生在画图时总会遇到很多障碍，要么漏了旋转中心，要么转错了方向。这时我们可以借助传统学具钟面，首先帮助学生厘清顺时针方向和逆时针方向，用手指跟着钟面转一转，将钟面的直观化为内心的抽象。然后再借助实物三角形，让学生先实际转一转、看一看（如图3），旋转后的图形在什么位置，与原图形之间有怎样的关系？为什么旋转出的图形位置会不同？学生在实际操作中，将感官和思维相结合，建立属于自己的空间观念。慢慢地，让他们脱离实物，在脑海中转一转、画一画，将旋转的过程内化。对于空间观念稍弱的同学，可以重复这样的过程，让学生在操作、想象中不断丰富对旋转的认识，提升他们的空间观念。

在学习“正方体的展开图”时，正方体模型就是不可缺少的传统学具。课前，学生用硬卡纸自主制作多个小正方体，并用胶带将每条棱都封好，在制作的过程中能够充分感受二维平面到三维立体的转变。课上，学生用剪刀将小正方体沿着不同的棱剪开，就可以得到它的展开图，这个过程与课前恰好相反，从立体又回到平面。在这一折一剪之间，学生的空间观念得到发展。当然，这里仅仅停留在操作上还不够，还可以采用多种方式拓展学生的思维。在学生剪开一部分正方体后，可以让学生先想象正方体展开后的图形，再试着剪一剪来验证自己的想法。同样，在折的过程中，也可以先出示展开图，让学生在脑海中折一折，再实际操作验证自己的想法。学生在想象——操作——想象的过程中，空间观念得到充分发展，深度达成学习目标。

3    运用传统学具，感受基本的数学思想

在解决问题的过程中，传统学具能够为学生提供具体的数学模型，借助形的表达理解数的关系，数的关系又影响着形的展示，帮助学生探寻解决问题的突破口，让问题得以解决。并在此过程中将不同的数学知识进行整合，数与形相结合，体会数学思想中重要的数形结合思想，提高学生的问题解决能力。

“分数与除法的关系”是学生在学习分数时遇到的一大难点。这两者之间的抽象联系与学生的形象思维构成了一对十分突出的矛盾。为此，在这部分知识的学习中，学具的使用显得尤为重要。在学生探索分数与除法的关系时，让学生用圆片分一分，涂一涂，借助形的表达理解数的计算。例如，“把3块饼平均分给4个小朋友，每个小朋友分得多少块？”列式3÷4，学生之前只学过两个整数能整除的除法。在不能整除的情况下，要么用小数表示结果，要么用余数，用分数表示是第一次。面对这样的问题，引导学生自己尝试用圆片分一分来帮助思考。3个圆片代表3块饼，平均分成4份，有两种基本思路：第一，一个圆片一个圆片地分（如图4-1），每个人都可以分得1个圆片的1/4，一共3个圆片，合起来就是3个1/4，也就是3/4。第二，将3个圆片叠在一起，直接平均分成4份（如图4-2），每份是3个的1/4，也是3/4。学生能够很好地借助这样的操作过程理解除法与分数的关系。这样的操作也为学生在解决不熟悉的问题时提供了基本思路。借助学具的直观表现，帮助学生理解抽象的数学知识，让数形结合这样的基本数学思想能够深入学生内心，并在实践中发扬光大，不断提升学生的数学思维。

在“钉子板上的多边形”的探索过程中，钉子板就是非常重要的传统学具。学生在研究了多边形内只有1颗钉子的情况下，进行猜想：是不是钉子板上任意多边形的面积都可以用边上的钉子數除以2？这时，学生可以充分利用手中的钉子板自主围出不同的多边形，让结论更具普遍性。结果，在验证过程中发现：有的多边形符合这样的猜想，有的却不符合。从而引导学生从变化中寻找不变的量。符合这样猜想的多边形还具有一个特征，那就是多边形内只有1颗钉子，由此完善结论。学生很快就思考：如果内部有2颗钉子呢？3颗呢？又会具有怎样的规律。这样的操作活动能够大大激发学生的学习热情。学生继续利用钉子板，围出合适的多边形，进行规律探索。在探索的过程中，充分感受数与形的紧密联系，体会基本的数形结合思想。

数学课程标准中也指出：要重视直观，处理好直观与抽象的关系。第二学段的学生在学习数学时，教师要创意使用传统学具，让学生通过观察表象、动手操作等直观方式不断获取感性认识，有效培养学生的观察能力和动手能力。学生在进行学具操作时，多种感官参与学习，激发学生主动思考、积极探索，提升学习兴趣，更容易找到解决问题的突破口，开阔学生的视野，提高问题解决能力，使直观操作最终促进学生抽象思维的发展。

当然，在什么时机使用什么学具，怎样使用学具才能够帮助学生更好地学习数学，这是教师需要提前思考的问题，也会随着教学评价的不断变化而有所调整。教师还可以根据自身的教学实际情况，改造一些已有的传统学具，让其更有利于学生操作与学习。

4    结语

总之，在第二学段数学课堂中，教师可以根据学习内容和学生的心理特点，把握好传统学具的使用契机，充分利用传统学具的直观性，给予学生动手操作的机会，帮助他们建立数学模型，将抽象的数学知识用直观的方式展示出来，厘清算理，建立空间观念，体会基本的数学思想，将学生的思维引向深处，培养学生的创新能力。

参考文献：

[1]孙兴华.小学数学传统学具的价值及运用[J].南京晓庄学院学报，2021，37（04）：17-21+121.

[2]宋蕊.小学数学中借助学具操作促进学生深度学习的思考[J].小学时代，2020（16）：21-23.

[3]黄志超.以操作为介 助推学生数学学习的深入[J].教育界，2021（20）：28-29.