对2021年高考数学上海卷第21题的探究

中山市桂山中学(528463) 蔡晓波 余铁青

一、题目再现与解答

题目1 (2021年高考上海卷第21题)已知f(x)是定义在R 上的函数,若对任意的x1,x2∈R,x1−x2∈S,均有f(x1)−f(x2)∈S,则称f(x)是S关联.

(1)判定和证明f(x)=2x+1 是否是[0,+∞)关联?是否[0,1]关联?

(2)若f(x)是{3}关联,当x∈[0,3)时,f(x)=x2−2x,解不等式2≤f(x)≤3

(3)证明:“f(x)是{1}关联,且是[0,+∞)关联”的充要条件是“f(x)是[1,2]关联”.

答案(1)是[0,+∞)关联; 不是[0,1] 关联; (2)[1+

本题是2021年高考上海卷压轴题.本题3个问题层层递进,第(1)(2)问较为容易,主要在于引导学生熟悉“S关联”的概念,第(3)问较为抽象,有一定的难度,因此第(1)(2)问的解答过程从略,以下主要对第(3)问的证法进行探讨.

证法1 必要性 根据条件可得f(x+1)=f(x)+1,故f(x+n)=f(x)+n.因为f(x)是[0,+∞)关联,对任何x1,x2∈R,当0≤x1−x2,有0≤f(x1)−f(x2),即当x1≤x2,时有f(x1)≤f(x2).

若1≤x1−x2≤2,则1+x2≤x1≤2+x2,所以f(1+x2)≤f(x1)≤f(2+x2),即f(x2)+1≤f(x1)≤f(x2)+2,即1≤f(x1)−f(x2)≤2,所以f(x)是[1,2]关联;

充分性 因为∀x1,x2∈R,当1≤x1−x2≤2 时,有1≤f(x1)−f(x2)≤2,所以1≤f(x+2)−f(x+1)≤2,

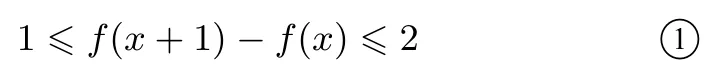
故2≤f(x+2)−f(x)≤4,又由1≤f(x+2)−f(x)≤2(因为1≤(x+2)−x≤2)可得:f(x+2)−f(x)=2,即f(x+2)−f(x+1)+f(x+1)−f(x)=2,结合①可得:f(x+2)−f(x+1)=1,f(x+1)−f(x)=1,故f(x)是{1}关联,故不难得出f(x+n)=f(x)+n.

∀x1,x2∈R,当0≤x1−x2,必存在n(n∈N)使得x1−x2∈[n,n+1],则x1−[x2+(n−1)]∈[1,2],因为f(x)是[1,2]关联,故1≤f(x1)−f[x2+(n−1)]≤2,即1≤f(x1)−f(x2)−(n−1)≤2,则有:f(x1)−f(x2)∈[n,n+1]⊆[0,+∞);故f(x)是[0,+∞)关联.

评注证法1 在证明f(x)是{1}关联时,巧妙的运用了不等式间的关系求出了f(x+1)−f(x)=1 的关系,实际上,利用反证法也可以证明出该关系.另外,结合f(x)是{1}关联与f(x)是[1,2]关联中的一边的不等式关系也是可以证出f(x)是[0,+∞)关联的,因此我们可得本题的另一种证法.

证法2 必要性同证法1.

充分性的证明与后边结论4 的证明类似,由读者自己整理.

以上是本题第(3)问的两种证法,本题的3个问题实际上都是在围绕这函数是某个值关联还是某个闭区间关联展开讨论的.那么我们不禁思考,本题的一般性结论是什么?函数S关联有没有其它性质?笔者对如上问题进行了一系列探讨.

二、问题的探究与推广

为行文分别,我们启用题目中的定义.

定义1 已知f(x)是定义在R 上的函数,若对任意的x1,x2∈R,x1−x2∈S 均有f(x1)−f(x2)∈S,则称f(x)是S关联.

(一)函数是某个值关联

如果f(x)是{a}(a为正实数)关联,则x1−x2=a且f(x1)−f(x2)=a,故当x1−x2=−a时f(x1)−f(x2)=−a,故f(x)是{−a}(a为正实数)关联,因此我们仅需讨论函数f(x)是非负数的关联即可.

对于函数关于某个值关联,我们不难得出如下结论:

结论1 任意定义在R 上的函数f(x)是{0}关联.

结论2 任意定义在R 上的函数f(x)是{a}(a为正实数)关联,则f(x)也是{ka},k∈Z 关联.

结论1 与2 比较容易证明,证明从略.

结论3 任意定义在R 上的函数f(x)是{a} 关联且是{b}关联(a,b为正实数),则f(x)也是{ma+nb},其中m,n∈Z.

证明由结论2 且f(x)是{b}关联可得:f(x+ma+nb)=f(x+ma)+nb,再由f(x)是{a} 关联可得:f(x+ma)=f(x)+ma,故f(x+ma+nb)=f(x)+ma+nb,故任意x1−x2=ma+nb,即x1=x2+ma+nb,故f(x1)=f(x2+ma+nb)=f(x2)+ma+nb,故f(x1)−f(x2)=ma+nb,故f(x)是{ma+nb}(m,n∈Z)关联.

几何意义如果函数f(x)是{a}(a为正实数)关联,则f(x+a)−a=f(x)(或f(x−a)+a=f(x)),故其几何意义为f(x)向左(右)平移a个单位,向下(上)平移a个单位后与原来图像重合,因此f(x)的图像呈类似于图1 的“类周期”性质,因此在实数范围内仅需知道f(x)在[m,n)(n−m=a)内的表达式(或图像)便可得出f(x)在R 上的表达式(或图像),题目1 的第(2)问就是考察这个性质.

图1

(二)函数关于某个连续闭区间关联

若函数f(x)是[−b,−a],(b>a>0)关联,则对于任意−b≤x1−x2≤−a均有−b≤f(x1)−f(x2)≤−a,这等价于:对于任意a≤x2−x1≤b均有a≤f(x2)−f(x1)≤b,故函数f(x)是[a,b]关联,因此下面我们着重研究函数f(x)是[a,b],(b>a>0)关联的情况.

由高中教材[2]可知,高中阶段我们所学的增函数的概念实际上是指严格增函数.关于增函数与严格增函数,在教材[1]的第16 页给出了如下定义:

定义2 设y=f(x),x∈D,如果对于任意x1,x2∈D,x1

在下文所说的增函数,均是符合定义2 的增函数.

题目1 的第(3)问提到了函数f(x)是[0,+∞)关联,故函数f(x)对于任意x1−x2≥0 则f(x1)−f(x2)≥0,容易分析可知f(x)在R 上是增函数.第(3)问同时给了我们提示,函数f(x)如果是具有某个特征的连续闭区间关联,则等价于该函数是某个值关联,且该函数是增函数,那么该“连续闭区间”必须具备什么特征呢?笔者探究得出如下结论:

结论4 设a∈R,a >0,则“f(x)是{a} 关联,且是[0,+∞)关联”的充要条件是“f(x)是[a,2a]关联”.

证明充分性 因为f(x)是[a,2a] 关联,所以当a≤x1−x2≤2a时,a≤f(x1)−f(x2)≤2a,即a+f(x2)≤f(x1)≤2a+f(x2),因为(x+a)−x∈[a,2a],故f(x)+a≤f(x+a),如果f(x)+a < f(x+a),则f(x+2a)=f(x+a+a)>f(x+a)+a>f(x)+2a.由于(x+2a)−x∈[a,2a],故f(x+2a)≤f(x)+2a,矛盾.故f(x+a)=f(x)+a,故f(x)是{a}关联.

结合结论2 得:f(x+na)=f(x)+na,n∈N.若x1−x2≥0,则存在n,(n∈N)使得x1−x2∈[na,(n+1)a],故x1−(x2+(n−1)a)∈[a,2a],结合f(x)是[a,2a] 关联,可得f(x1)−f(x2+(n−1)a)≥a,f(x1)−f(x2)≥a+(n−1)a=na≥0,故f(x)是[0,+∞)关联.

结论4 的必要性的证明方法类似于解法1 必要性的证明,此处从略.

显然,当a=1 时便为题目1 的第(3)问.因此,上述结论4 的证明过程中,令a=1 便可得第(3)问充分性的第二种解法.

结论5 设a∈R,a >0,则有:“f(x)对于任意n∈N是[na,(n+1)a]关联”充要条件为:“f(x)是[a,2a]关联”

证明充分性 对于任意n∈N,设na≤x1−x2≤(n+1)a,则a≤x1−(x2+(n−1)a)≤2a,又因为f(x)是[a,2a]关联,所以a≤f(x1)−f(x2+(n−1)a)≤2a.

结合结论2,4 可得:f(x)是[a,2a] 关联,则f(x)是{na},n∈N 关联,故f(x2+(n−1)a)=f(x2)+(n−1)a,故na≤f(x1)−f(x2)≤(n+1)a,所以f(x)是[na,(n+1)a]关联.显然令n=1 可得必要性.

结论6 设a∈R,a >0,“f(x)是[a,2a]关联”的充要条件是“f(x)是[a,na](n为常数,且n≥2,n∈N)关联”.

证明必要性 若a≤x1−x2≤na(n≥2,n∈N),则存在k∈N,2≤k≤n使得(k−1)a≤x1−x2≤ka,因为f(x)是[a,2a]关联,由结论5 可得:f(x)也是[(k−1)a,ka]关联,故a≤(k−1)a≤f(x1)−f(x2)≤ka≤na,故f(x)是[a,na](n为常数,且n≥2,n∈N)关联.

充分性 因为f(x)是[a,na] (n为常数,且n≥2,n∈N)关联,故对于任意a≤x1−x2≤na均有a≤f(x1)−f(x2)≤na,又因为x+a−x=a∈[a,na],故a≤f(x+a)−f(x),即f(x)+a≤f(x+a),故对于任意k∈N,1≤k≤n有:

即有

同理可得:f(x−ka)≤f(x)−ka,故f(x+ka)=f(x+na−(n−k)a)≤f(x+na)−(n−k)a,另一方面x+na−x=na∈[a,na],故f(x+na)−f(x)≤na,即f(x+na)≤f(x)+na,故f(x+ka)≤f(x+na)−(n−k)a≤f(x)+na−(n−k)a=f(x)+ka,即

由②③可得:f(x+ka)=f(x)+ka,故f(x+a)=f(x)+a,即f(x)是{a}关联.此外,对任意x1−x2≥0,存在m,(m∈N)使得x1−x2∈[ma,(m+1)a],故x1−(x2+(m−1)a)∈[a,2a]⊆[a,na],故f(x1)−f(x2+(m−1)a)≥a,即f(x1)−f(x2)−(m−1)a≥a,故f(x1)−f(x2)≥ma≥0,所以f(x)是[0,+∞)关联,由结论4 可知:f(x)是[a,2a]关联.

结论4,5,6 反映了如下的关系:“f(x)是{a}关联,且是[0,+∞)关联”⇔“对于任意n∈N+,f(x)是[na,(n+1)a]关联”⇔“f(x)是[a,2a]关联”⇔f(x)是[a,na](n≥2,n∈N)关联.

几何意义对于f(x)是[a,b](b > a >0)关联,则a≤x1−x2≤b,且a≤f(x1)−f(x2)≤b,即x2+a≤x1≤x2+b且f(x2)+a≤f(x1)≤f(x2)+b.如图2,结合图像可得f(x)是[a,b](b>a>0)关联的几何意义是在函数f(x)上任意一点(x0,f(x0))距离的右上角画一个边长为b−a的正方形,则函数f(x)在[x0+a,x0+b]之间的图像完全落在该正方形内.

图2

结合几何意义,我们不难得出如下结论:

结论7 设f(x)是定义在R 上的函数,则“对任意a>0,f(x)是[a,2a] 关联”的充要条件是“f(x)=x+c(c为常数)”.

证明充分性较为容易证明,故这里不再赘述.

必要性 因为对于任意的a >0,f(x)是[a,2a] 关联,由结论5 可得:对∀k∈Z,f(x)是{ka}关联,即f(x+ka)=f(x)+ka,注意到a的任意性与k∈Z 可得:f(x+m)=f(x)+m(m∈R),故对于任意x0∈R,有

(三)结论4 的应用

设a∈R,a >0,则“f(x)是{a}关联,且是[0,+∞)关联”的充要条件是“f(x)是[a,2a]关联”

结论4 告诉我们一个函数若满足f(x+a)=f(x)+a其中a∈R+为常数且f(x)是增函数,则当a≤x1−x2≤2a时,便有a≤f(x1)−f(x2)≤2a的不等式关系.因此,如果我们对f(x)赋予具体的表达式便可得到具体的不等式,比如:对于函数f(x)=(x−k)p+k,x∈[k,k+1),k∈Z,p为正常数,显然就是满足f(x+1)=f(x)+1 且f(x)是增函数,则f(x)是[1,2] 关联,则我们适当选取值,比如令x1=m+,x2=m+,m为常数,故,因此有以上分析相当于如下习题:

习题已知f(x)=(x−k)p+k,x∈[k,k+1),k∈Z,p为常实数,且p>0,求证:对于任意成立(m为常数).

三、结语

至此,我们对2021年高考上海卷第21题进行了一系列的探究,得出了函数S关联的一些结论,但是仍然有一些问题未能解决,略感遗憾,比如:

问题1 定义在R 上的函数f(x)是[a,b](b >2a >0)关联,那么能否得出f(x)是[0,+∞)关联呢?如果不能那么能否举出反例,如果能,该怎么证明?

问题2 在“结论4 的应用”分析中,笔者用了函数f(x)=(x−k)p+k,x∈[k,k+1),k∈Z,其本质实际是一个分段函数,能否找到一个由初等函数构造而成,且非分段的具体的非隐函数f(x),使得f(x)是[a,2a](a >0)关联呢?如果能找到,那么得到的不等式将更加具体.