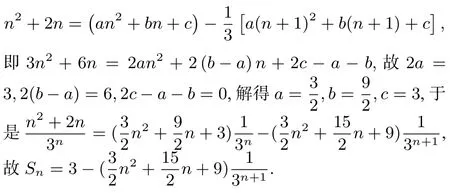对于{anqn}类型数列求和的思考

广东省中山市中山纪念中学(528454) 李文东

一.试题呈现

在笔者的教学中碰到如下三个数列问题.

问题1 等比数列{an}的各项均为正数,2a4,a3,4a5成等差数列,且a3=2a22.

(1)求数列{an}的通项公式;

问题2 数列{bn} 的前n项和为Sn,bn+1=Sn+2,b1=2.

(1)求数列{bn}的通项公式;

(2)已知an=log2bn,cn=,求数列{cn}的前n项和Tn.

问题3 已知数列{an} 的前n项和为Sn,且Sn=n2+5n+8,数列{bn}满足:b1=6.bn+1=

(1)求数列{an}和{bn}的通项公式;

上述问题求解过程如下:

问题1解答(1)数列{an}的通项公式为

(2)由(1),得

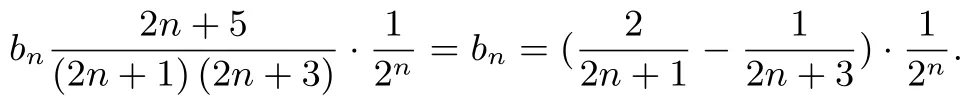
所以

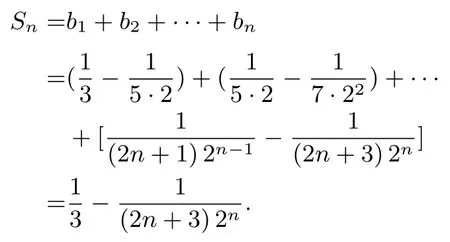
故数列{bn}的前n项和Sn=

问题2解答(1)bn=2n.

问题3解答(1)a1=14,an=2n+4(n≥ 2),bn=3n2n.

(2)当n=1 时,;当n≥2 时,

故

二.规律探究与推广

可以看到,上述问题均属于{anqn}(q >0 且q≠1)类型数列求和问题,那么上述裂项求和是怎么想到的呢?其内在规律是什么?数列求和必研究通项,我们仔细观察上述三个求和问题中数列的通项的特点,可以发现:

对于问题1,注意到2n+1,2n+3 与2n+5 构成等差数列,即2n+5=2(2n+3)−(2n+1),从而

将上述问题一般化,我们有下面的结论:

结论1 设{an}(an≠0)为等差数列,则

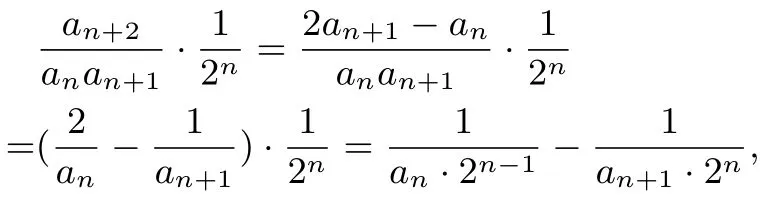
结论2 对任意的数列{an}(an≠0),

对于问题2,注意到:2n−1=3n−(n+1),故

类比问题1 的推广,我们有下面的结论:

结论3 对任意的数列{an}(an≠0),

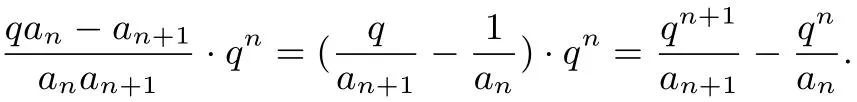
类似的将问题3 一般化,我们有下面的结论:

结论4 对任意的数列{an}(an≠0),

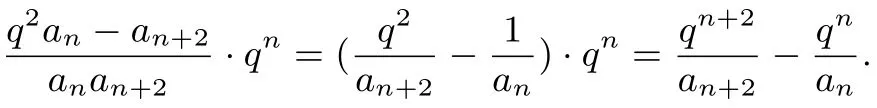
结论5 对任意的数列{an}(an≠0),k∈N∗,

运用上述结论,我们可以编制如下问题:

例1 求数列的前n项和Sn.

解

于是

三.方法拓展与应用

一般地,对于数列{anqn} (q >0 且q≠1),可以考虑如下的裂项方式求和:设an=q ·f(n+1)−f(n),则anqn=[q·f(n+1)−f(n)]qn=f(n+1)qn+1−f(n)qn,从而[f(i+1)qi+1−f(i)qi]=f(n+1)qn+1−f(1)q.其中f(n)可由an的特征采用待定系数法确定.

例2 求等比数列{an}(公比q≠1)的前n项和,即Sn=.

解由于qn前面的系数为常数1,因此待定部分的f(n)也为常数,设为A,因此1=Aq−A,则,于是qn=(Aq−A)qn=Aqn+1−Aqn,从而

例3 求数列{(2n+1)3n}的前n项和Sn.

解设2n+1=3[a(n+1)+b]−(an+b),即2n+1=2an+3a+2b,故3a+2b=1,2a=2,解得a=1,b=−1.故(2n+1)3n=[3n−(n−1)]3n=n·3n+1−(n−1)·3n,故

例4 求数列的前n项和Sn.

解设