运用数形结合思想求根式函数值域或最值例析

江苏省扬州市扬州大学(225002) 陈蕾伊

根式函数值域或最值问题具有题型灵活多变,涉及知识面广,解决方法多而巧的特点.它考察了学生观察、联想、类比、转换等能力,不仅是学生学习的难点,也一直是高考和竞赛的热点.本文将利用数形结合思想,把数或数量关系与图形一一对应起来,“以形助数”,通过观察根式函数的特点,把其转换为距离、斜率、截距、向量、图形面积,充分利用几何信息,快速解决问题.

一、运用距离

(一)运用两点间距离

将根式下的函数分别进行配方把原函数转换成为

形式,构造成两点间距离是解决双根式函数值域或最值问题最常见的做法,把根式函数值域或最值问题转换为了某线上的动点与两定点之间的距离之和或之差的范围问题.

例1求函数的值域.

分析将原函数配方转换为

其几何意义是x轴上的动点P(x,0)到两定点A(0,2),B(1,−3)的距离之和.求其值域,只需求出最值.由图1 可知,当A,P,B三点共线时,有最小值,无最大值.

图1

解将原函数变形得到y=,这表示x轴上的动点P(x,0)到两定点A(0,2),B(1,−3)的距离之和.因为|PA+PB|≥|AB|(当A,B,P三点共线时,取等号),所以y≥|AB|=.故函数的值域为.

例2 求函数f(x)的最大值,其中

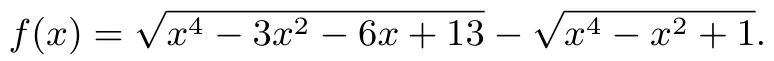
分析将原函数配方变为

其几何意义是抛物线y=x2上的动点P(x,x2)到两定点A(3,2),B(0,1)的距离之差,由图2 可知,当P位于P′时,函数取得最大值|AB|(P,A,B不共线时可构成一个三角形,三角形任意两边差小于第三边).

图2

解

表示动点P(x,x2)到两定点A(3,2),B(0,1)的距离之差,即f(x)=|PA|−|PB|,因为点P(x,x2)的轨迹是抛物线y=x2,B在抛物线内,A在抛物线外,所以当点P,B,A三点共线且点B在AP之间时(即图2 点P′)|PA|−|PB|最大,为|AB|(P,A,B不共线时可构成一个三角形,三角形任意两边差小于第三边).而|AB|=,所以函数f(x)的最大值是.

(二)运用点到直线距离

我们通常利用点到直线距离来解决一类含绝对值的根式函数值域或最值问题.构造一个一次函数,使原函数可以表示成一个动点到直线的距离,从而利用几何特征来求出其值域或最值.

例3 求函数f(x)=的值域.

分析构造一条直线l:x−y+4=0,则动点(动点P的轨迹是一个半圆)到直线l的距离d=,故f(x)=,观察图3,由几何特征可以求出d的最值,也就找到了函数的值域.

解因为,所以可视为动点到直线l:x−y+4=0 的距离d.又因为P的轨迹是一个半圆:x2+y2=2,观察图3,根据几何特征,可知:当P位于P′时,有dmin=|CP′|=; 当P位于P′′时,有dmax=|CP′′|=故函数f(x)=的值域为.

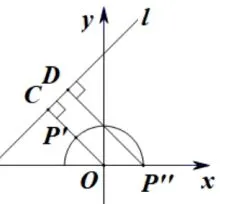
图3

(三)运用两条平行直线间距离

此种方法适合y=f(x)+g(x)(其中f(x)是一个一次函数,g(x)是一个根式函数)型函数,把g(x)进行换元,化简则得到一条二次曲线,过原点作与f(x)同斜率的直线l1,平移该直线与二次曲线相切得到新的直线l2,两条平行直线之间的距离就是函数的最小值,无最大值.

例4 求的值域.

分析令(双曲线的一支),则u=+y,作x轴的垂线与交于A、B两点.观察图像四可知,原函数的最小值就是|AB|的最小值,无最大值.

解令u=(u≥0),则16u2−4x2=3 是双曲线的上支.作x轴的垂线与交于A、B两点,由图4 可知,直线u=+b(b>0)与直线平行,当与相切于点B时,|AB|有最小值b,就是原函数y的最小值.

图4

二、运用斜率

解决分式无理函数值域问题,我们通常可以利用斜率来求解,构造出这样的模型,从而将函数值域问题转化为某曲线上的动点与一定点连线的斜率的范围问题[1].

例5 求函数f(x)=的值域.

分析观察函数f(x)可以发现f(x)是动点到定点A(−1,−2)连线的斜率,而P的运动轨迹是(x−2)2+y2=1(其中y≥0),因此f(x)值域问题转换为了半圆上一动点P到定点A连线的斜率范围问题.观察图4 可知,当P位于P′时,斜率最小;当P位于P′′时,AP′′与半圆相切,斜率最大,即可求出原函数值域.

图5

解令y=,则有(x−2)_2+y2=1(其中1≤x≤3,0≤y≤1),故f(x)=,其几何意义是半圆上一动点P到定点A(−1,−2)连线的斜率,所以函数值域问题就是PA斜率范围问题.

观察图形易知:当P位于P′时,斜率最小,kAP′=; 过A作半圆的切线与半圆交于P′′,设AP′′的方程为y+2=k(x+1),则圆心(2,0)到直线的距离为d==1,解得k=,由图像可知k=,斜率最大值为k=.故函数f(x)的值域为.

三、运用线性规划

看到含根式函数,可以把带根部分的函数进行换元替换,从而把原函数变成一个一次函数(目标函数),新的变量通过化简构成圆或二次曲线的一部分(约束条件),求函数值域问题就转化成了线性规划求截距最值问题.此种方法适合y=ax+b±(ac≠0)、y=(ac≠0)、y=ax+b ±(ac≠0)、y=ax2+bx+c±(ad≠0)型函数[2].

例6 求函数的值域.

分析令则有u2+v2=9(u,v≥ 0),y=u+利用线性规划方法,那么u2+v2=9、u≥0、v≥0 是三个约束条件,u=是目标函数,可行域就是第一象限的圆弧,如图6 所示,则函数的值域就是目标函数过圆弧时y的截距范围.

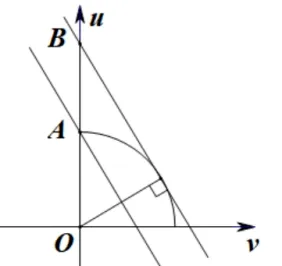
图6

解令,则有u2+v2=9 (u,v≥0),u=因此,函数值域问题就转变成了过圆弧上的点且斜率为的直线系的截距范围问题.

四、运用向量

利用向量求解根式函数值域问题,就是构造向量,通过函数等价于向量数量积,从而由向量夹角的范围求出函数值域.此种方法可以解决(其中f(x)+g(x)=c)型函数,构造向量a=(m,n),b=,则原函数就等价于y=a·b=|a||b|cos〈a,b〉,而构造的向量模为定值,所以结合图像求出两向量夹角〈a,b〉范围也就求出了函数的值域[3].

例7 求的值域.

分析观察函数可以发现2x2−1+5−2x2=4,可以直接利用向量法求解.令a=(1,1),b=,则|a|=,|b|=2,所以y=a·b=|a||b|cos〈a,b〉,显然b的终点在以(0,0)为圆心,半径为2 的圆弧上,观察图7 可知,〈a,b〉∈,cos〈a,b〉∈,则可求出函数的值域.

解令a=(1,1),b=,则|a|=,|b|=2,因为=4,所以b的终点在以(0,0)为圆心2 为半径的圆弧上,由图7 可知,〈a,b〉∈,cos〈a,b〉∈,所以y==a·b=|a||b|cos〈a,b〉∈.

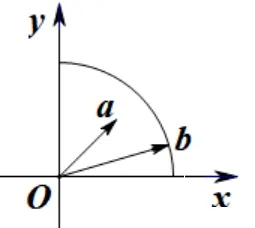
图7

五、运用图形面积

利用图形面积只能解决根式函数最值问题,最重要的就是构造一个合适的几何图形.首先需要对根式下的函数进行因式分解,使图形的边长长度为分解后的单因式,通过面积的等式关系使原函数化为一条边与一个未知角度的三角函数值乘积,由三角函数值的性质求出函数的最大值.此种方法具有特殊性,下面例举说明.

例8 求函数f(x)的最大值,其中

分析−x2+10x−9=(x−1)(9−x),−x2+68x−256=(x−4)(64−x),这四个单因式各不相同,因此考虑构造一个梯形,如图8 所示.由S梯形ABCD=S∆ABE+S∆CDE+S∆AED,可以化简得到=AE·ED·sin ∠AED,即f(x)=AE·ED·sin ∠AED,根据三角函数性质可以求出原函数的最大值.

图8

解构造直角梯形ABCD,使得AB=,CD=,BC=BE+EC=如图8,由S梯形ABCD=S∆ABE+S∆CDE+S∆AED,知

于是f(x)=·sin ∠AED,故f(x)≤=.故f(x)的最大值为