高考导数模块过关卷答案与提示

一、选择题

1.D 2.C 3.A 4.C 5.B 6.C 7.C 8.A 9.B 10.B 11.C 12.A 13.A 14.C 15.B 16.C 17.B 18.A 19.C 20.D 21.B 22.A 23.D 24.B 25.B 26.D 27.B 28.C 29.D 30.C 31.D 32.D 33.D 34.C 35.D 36.C 37.D 38.A 39.A

二、填空题

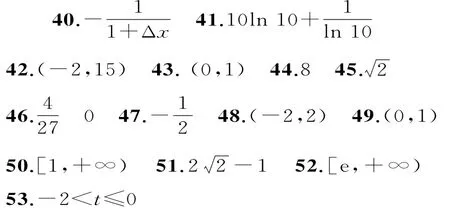
三、解答题

54.因为f(x)=x3+ax2+bx+1,所以f'(x)=3x2+2ax+b。

令x=1,得f'(1)=3+2a+b。又f'(1)=2a,所以3+2a+b=2a,b=-3。

令x=2,得f'(2)=12+4a+b。又f'(2)=-b,所以12+4a+b=-b。

55.(1)当a=-2时,f(x)=x3-32x2+3x+1,则f'(x)=3x2-62x+3。

令f'(x)=0,解得x1=2-1,x2=2+1。

当x∈(-∞,2-1)时,f'(x)＞0,f(x)在(-∞,2-1)上是增函数;

当x∈(2-1,2+1)时,f'(x)＜0,f(x)在(2-1,2+1)上是减函数;

当x∈(2+1,+∞)时,f'(x)＞0,f(x)在(2+1,+∞)上是增函数。

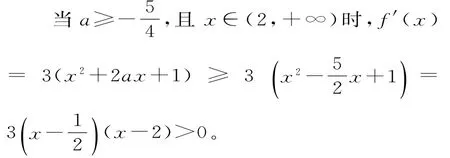
所以f(x)在(2,+∞)上是增函数,于是当x∈[2,+∞)时,f(x)≥f(2)≥0。

56.(1)由题意知x∈(0,+∞)。因为f(x)=a(x-5)2+6lnx,所以f'(x)=2a(x-5)+。

令x=1,得f(1)=16a,f'(1)=6-8a。

所以曲线y=f(x)在点(1,f(1))处的切线方程为y-16a=(6-8a)(x-1)。

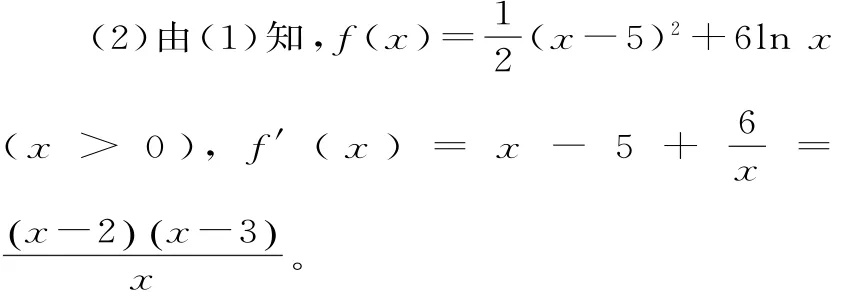
令f'(x)=0,解得x1=2,x2=3。

当0＜x＜2或x＞3时,f'(x)＞0,故f(x)在(0,2)和(3,+∞)上为增函数;

当2＜x＜3时,f'(x)＜0,故f(x)在(2,3)上为减函数。

57.(1)因为f(x)在区间(0,+∞)上是单调增函数,所以-m2+2m+3＞0。故m2-2m-3＜0,解得-1＜m＜3。又m∈Z,所以m=0,1,2。

而m=0或2时,f(x)=x3不是偶函数,m=1时,f(x)=x4是偶函数,所以f(x)=x4。

很显然x=0不是方程x2+3ax+9=0的根。

为使g(x)仅在x=0处有极值,必须x2+3ax+9≥0恒成立,即有Δ=9a2-36≤0。

解不等式得a∈[-2,2]。

这时,g0()=-b是唯一极值,所以a∈[-2,2]。

58.(1)由题意可知f(x)的定义域为(0,+∞)。

因为a＞2,所以a-1＞1。

故当1＜x＜a-1时f'(x)＜0;

当0＜x＜1或x＞a-1时f'(x)＞0。

故函数f(x)在区间(1,a-1)上单调递减,在区间(0,1)和(a-1,+∞)上单调递增。

(2)由a=1知g(x)=x3+x2-2x,所以Sn=n3+n2-2n。

综上,不等式得证。

(2)令F(x)=f(x)-(x-1),x∈(1,+∞)。

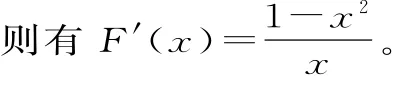
当x∈(1,+∞)时,F'(x)＜0,所以F(x)在[1,+∞)上单调递减。

故当x＞1时,F(x)＜F(1)=0,即当x＞1时,f(x)＜x-1。

(3)由(2)知,当k=1时,不存在x0＞1满足题意。

当k＞1时,对于x＞1,有f(x)＜x-1＜k(x-1),则f(x)＜k(x-1),从而不存在x0＞1满足题意。

当k＜1时,令G(x)=f(x)-k(x-1),x∈ (1,+∞)。

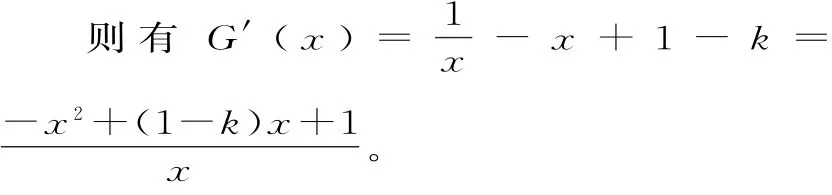
由G'(x)=0,得:

-x2+(1-k)x+1=0。

60.(1)当a=1时,f(x)=x3-1,f(2)=3。

f'(x)=3x2-3x,f'(2)=6,所以曲线y=f(x)在点(2,f(2))处的切线方程为:

y-3=6(x-2),即y=6x-9。

(2)f'(x)=3ax2-3x=3x(ax-1)。令f'(x)=0,解得x=0或x=

当x∈ (1,x2)时,G'(x)＞0,故G(x)在[1,x2)内单调递增。

从而当x∈ (1,x2)时,G(x)＞G(1)=0,即f(x)＞k(x-1)。

综上,k的取值范围是(-∞,1)。

以下分两种情况讨论:

当x变化时,f'(x),f(x)的变化情况如表1:

表1

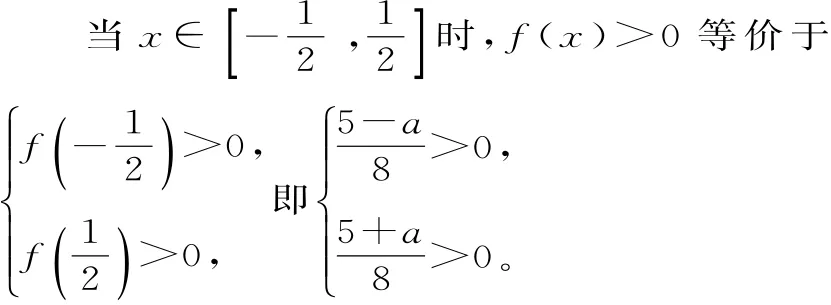
解不等式组得-5＜a＜5。

因此,0＜a≤2。

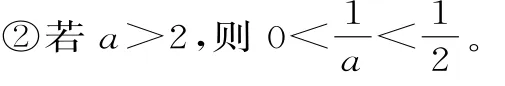
当x变化时,f'(x),f(x)的变化情况如表2:

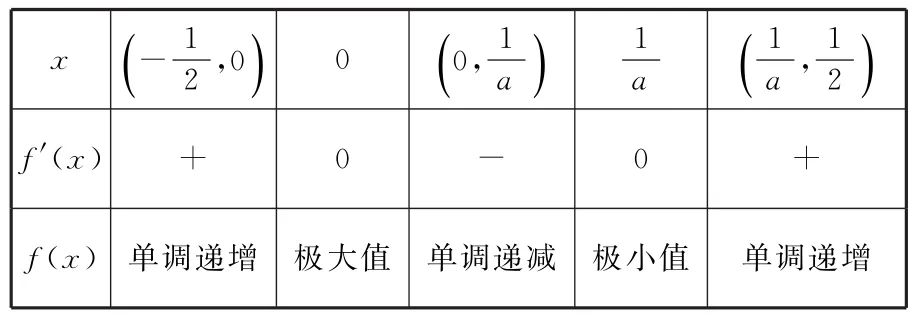
表2

综合①②,a的取值范围为0＜a＜5。