为数学点赞——名师例析数学文化（2）微积分篇

■北京市第十二中学高中部　高慧明

■北京市教育学院丰台分院　张 琦

本刊特邀栏目专家简介:

高慧明 首届全国十佳班主任,全国著名数学特级教师,国家教育部课程改革“全国先进工作者”,全国著名高考数学命题与考试研究专家,国家教育部“国培计划”全国中小学教师培训、班主任培训、校长培训特邀主讲专家,受邀在全国各地做有关高考科学备考、班级管理等多场专题报告。现任教于北京市第十二中学高中部。

《普通高中数学课程标准(征求意见稿)》(2016)在《选修Ⅰ课程》中《一元函数导数及应用》这一章明确要求同学们要“收集对微积分的创立和发展起重大作用的有关资料,包括一些重要历史人物(牛顿、莱布尼茨、柯西、魏尔斯特拉斯等)和事件,采取独立的方式或者小组合作的方式,完成一篇有关微积分创立与发展的研究报告”。

微积分基本可以看作初等数学和高等数学的分水岭,它充分体现了人类抽象思维的魅力和强大。那么接下来我们就来看看微积分的发展简史吧。

一、微积分思想的萌芽

有人曾指出,自然科学史上以令人惊叹的创造性方式工作的三大科学巨匠是古希腊的阿基米德(Archimedes)、17世纪英国的牛顿(Newton)和20世纪德国的爱因斯坦(Einstein)。根据1906年重新发现的阿基米德羊皮卷古抄本,早在公元前200多年,阿基米德就已经将积分想法广泛应用于处理图形的面积、物体体积等问题。我们可以认为阿基米德已经掌握了我们后世称之为积分学的精髓。

我们来看看阿基米德如何使用“穷竭法”求抛物线面积的(《抛物线求积》命题24)。他的证明如下:

如图1,C是弓形ACB的顶点,以△ABC的两边AC和BC为新的底截弓形,得顶点D和E,阿基米德在引理中从几何上证明了新增的面积为△ABC面积的。继续使用AD,DC,CE,EB为新的底来截弓形,依此类推,阿基米德指出后一次新增面积是前一次新增面积an,来代表这些面积,其中最大面积a1等于m(S△ABC)。随着n的增大,多边形面积将越来越接近弓形的面积。阿基米德经过巧妙的代,其中Sn表示前n项面积的和,也即弓形的内接多边形的面积。经过数学处理,阿基米德算得弓形面积等于

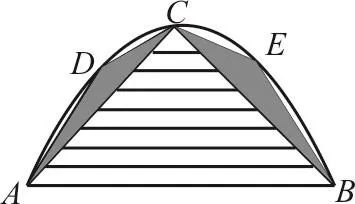
图1

在上述使用“穷竭法”证明的过程中,阿基米德清楚地向我们展示了处理此类问题的微积分思想,即先将不可求量拆成小的可求量(微分思想),再将这些小量累加求和(积分思想)。

二、微积分思想产生的时代背景

16、17世纪,科学急速发展。此时初等数学已不能满足社会的需要,在这一阶段中,许多科学问题亟待解决,这些问题也就成了促使微积分产生的因素。归结起来,大约有四种主要类型:第一类是研究运动的时候直接出现的瞬时速度问题;第二类是求曲线的切线的问题;第三类是函数的最大值和最小值问题;第四类是曲线围成图形的面积、曲面围成几何体的体积等问题。

三、微积分的产生与发展

一般认为,英国科学家牛顿和德国数学家莱布尼茨(Leibniz)分别在自己的国度里独自研究和完成了微积分的创立工作。他们的功绩主要在于:

1.把各种问题的解法统一成一种方法,微分法和积分法;

2.有明确的计算微分法的步骤;

3.证明了微分和积分互为逆运算。

牛顿对微积分问题的研究始于1664年秋,他的第一个微积分短评是于1669年在《运用无限多项方程的分析学》里给出的。在这部专著里他运用了无穷小量,并通过二项式定理扩展了其适用性。在这篇论文中,牛顿运用了一个无穷小矩形或者面积“瞬”的概念,并且发现了曲线的面积。在这本书里,牛顿介绍了他特有的符号和概念。牛顿把变化率称为流数,用字母上加点的“标记字母”表示;他称变化的量为流量。牛顿将自古希腊以来求解无限小问题的各种特殊技巧统一为两类普遍的算法——正、反流数术亦即微分与积分,并证明了二者的互逆关系进而将这两类运算逐步统一成一个整体。1687年牛顿发表了他的具有划时代意义的科学名著《自然哲学的数学原理》,流数术(即微积分)是其三大发现之一。

相比于牛顿的工作,莱布尼茨的创造性工作的数学特征更加明显。1675-1676年间,他从求曲边形面积出发得到积分的概念。1684年莱布尼茨发表了数学史上第一篇正式的微积分文献《一种求极限值和切线的新方法》。这篇文献是他自1673年以来对微积分研究的概括与成果,其中叙述了微分学的基本原理,认为函数的无限小增量是自变量无限小变化的结果,且把这个函数的增量叫作微分,用字母d表示,并得到广泛使用。还给出了和、差、积、商及幂的微分法则。同时包括了微分法在求切线、极大值、极小值及拐点方面的应用。两年后,他又发表了一篇积分学论文《深奥的几何与不变量及其无限的分析》,其中首次使用积分符号“∫”,初步论述了积分问题与微分求切线问题是互逆问题。这就是今天大家熟知的牛顿-莱布尼茨公式(x)dx=F(b)-F(a),为我们勾画了微积分学的基本雏形和发展蓝图。

牛顿建立微积分是从运动学的观点出发,而莱布尼茨茨则从几何学的角度去考虑,所创设的微积分符号远远优于牛顿的符号,并有效地促进了微积分学的发展,莱布尼茨第一个表达出微分和积分之间的互逆关系。将微分和积分统一起来,是微积分理论得以建立的一个重要标志。

四、微积分与第二次数学危机

由于运算的完整性和应用范围的广泛性,微积分成为了解决问题的重要工具。同时关于微积分基础的问题也越来越严重。以求速度为例,瞬时速度是当Δt趋向于零时的值。但是Δt是零,是很小的量,还是什么东西?这个无穷小量究竟是不是零?这引起了极大的争论,引起了学界对微积分基础的质疑,从而引发了第二次数学危机。

由于数学家成功地用微积分解决了许多实际问题,因此有些人就对这些基础问题的讨论不感兴趣。如达朗贝尔(JeanleRond d'Alembert)就说,现在是“把房子盖得更高些,而不是把基础打得更加牢固”。

五、第二次数学危机的慷慨赠与

微积分的严格化工作经过近一个世纪的尝试,到19世纪初已开始显现成效。对分析的严密性真正有影响的先驱则是伟大的法国数学家柯西(Cauchy)。柯西在数学上的最大贡献是在微积分中引进了极限概念,并以极限为基础建立了逻辑清晰的分析体系。这是微积分发展史上的精华,也是柯西对人类科学发展所做的巨大贡献。与此同时,柯西还在此基础上创建了复变函数的微积分理论。

柯西对定积分作了最系统的开创性工作,他把定积分定义为和的“极限”。在定积分运算之前,强调必须确立积分的存在性。他利用中值定理首先严格证明了微积分基本定理。柯西关于分析基础的最具代表性的著作是他的《分析教程》(1821)、《无穷小计算教程》(1823)以及《微分计算教程》(1829),它们以分析的严格化为目标,对微积分的一系列基本概念给出了明确的定义,在此基础上,柯西严格地表述并证明了微积分基本定理、中值定理等一系列重要定理,定义了级数的收敛性,研究了级数收敛的条件等,他的许多定义和论述已经非常接近于微积分的现代形式。柯西的工作在一定程度上澄清了在微积分基础问题上长期存在的混乱,向分析的全面严格化迈出了关键的一步。