极值点偏移问题破解策略

■甘肃省秦安县第二中学　罗文军

一、极值点偏移的概念

1.极值点不偏移

已知函数y=f(x)是连续函数,在区间(x1,x2)上有且只有一个极值点x0,且f(x1)=f(x2),若极值点左右的“增减速度”相同,,我们称这种状态为“极值点不偏移”(如图1)。

2.极值点偏移

已知函数y=f(x)是连续函数,在区间(x1,x2)上有且只有一个极值点x0(即y=f(x)为单峰函数),且f(x1)=f(x2),若极值点左右的“增减速度”不同,函数的图像不具有对称性,常有极的情况,我们称这种状态为“极值点偏移”(如图2)。

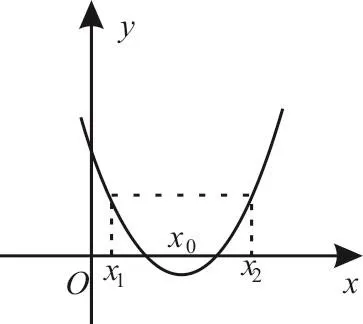
图1

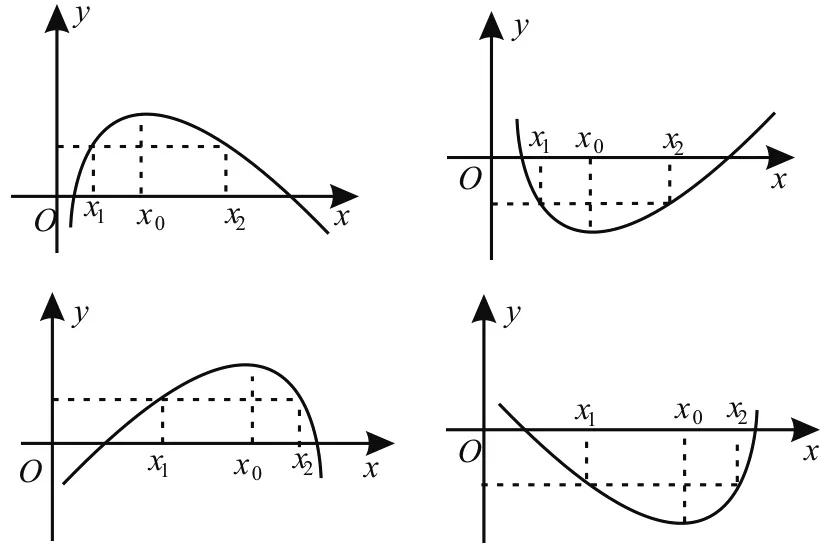
图2

二、解题策略

1.比值(差值)代换

运用比值(差值)代换法不需要讨论所给函数的单调性,也不需要求出参数的取值范围,而是直接根据题意列出方程,然后结合分析法消去参数,得出只含有x1和x2的等式或者不等式,最后通过比值(差值)代换,构造新函数,证明不等式。

(甘肃省兰州第一中学2018届高三第一次模拟试题)

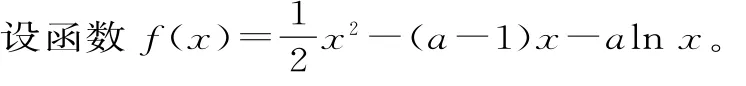
(1)讨论函数f(x)的单调性;

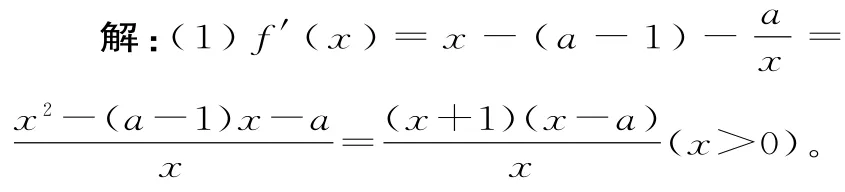
①当a≤0时,f'(x)＞0恒成立,所以f(x)在(0,+∞)上单调递增。

②当a＞0时,解f'(x)＞0得x＞a,解f'(x)＜0得0＜x＜a。所以f(x)在(0,a)上单调递减,在(a,+∞)上单调递增。

综上,当a≤0时,f(x)在(0,+∞)上单调递增;当a＞0时,f(x)在(0,a)上单调递减,在(a,+∞)上单调递增。

(2)f(x)=b有两个不相等的实数根x1,x2,不妨设0＜x1＜x2。

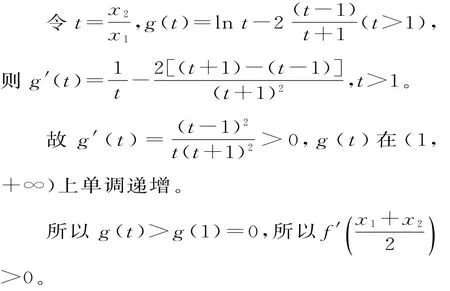
点评:本题第一问考查了利用导数研究含参函数的单调性问题,运用了分类讨论的思想方法;第二问利用导数研究函数的极值点偏移问题,运用了比值代换法。

(2017年福建省八校适应性考试)已知函数f(x)=x-aex(a∈R,e为自然对数的底数),若函数f(x)有两个不同的零点x1,x2,求证:x1+x2＞2。

证明：函数f(x)有两个不同的零点x1,x2,所以x1=aex1,x2=aex2。

记h(t)=(t-2)et+t+2(t＞0),则h'(t)=(t-1)et+1。

记m(t)=(t-1)et+1,则m'(t)=tet。当t＞0时,m'(t)＞0,m(t)＞m(0)=0,h'(t)＞0,h(t)＞h(0)=0。

故(t-2)et+t+2＞0成立,x1+x2＞2。

点评:本题解法运用了差值代换法,没有讨论所给函数的单调性,也没有求出参数a的取值范围,而是直接根据题意列出两个方程,然后对两个方程相加减,并结合分析法消去参数得出只含有x1,x2的不等式,最后通过差值代换,构造新函数,再二次求导,证明不等式。

对于极值点偏移问题,如果原函数的解析式中含有lnx,那么通常考虑用比值代换法;如果原函数的解析式中含有ex,那么可以考虑用差值代换法。

2.构造差函数法

构造差函数破解函数极值点的偏移问题的基本步骤为:

(1)求出函数f(x)的极值点x0。

(2)构造一元差函数F(x)=f(x)-f(2x0-x);

(3)对差函数F(x)求导,判断其导数的符号,确定F(x)的单调性;

(4)结合F(x0)=0,判断F(x)的符号;

(5)由f(x1)=f(x2)＞f(2x0-x1)(或＜f(2x0-x1),结合f(x)的单调性得到x2＞(或＜)2x0-x1,从而确定＜)x0。

(2017年河北省石家庄市二检)已知函数f(x)=xlnx+x2-ax+2,其中a∈R,若f(x)有两个零点x1,x2,求证:x1+x2＞2。

令g'(x)=0,得x=1或-2(舍去)。

当0＜x＜1时,g'(x)＜0,当x＞1时,g'(x)＞0。

故g(x)在(0,1)上为减函数,在(1,+∞)上为增函数,x=1为g(x)的极小值点。

若f(x)有两个零点x1,x2,不妨设x1＜x2,则0＜x1＜1＜x2。

当x∈(0,1)时,G'(x)＜0,G(x)单调递减,G(x)＞G(1)=0。

g(x2)=g(x1)＞g(2-x1),所以x2＞2-x1,即x1+x2＞2。

点评:本题属于导数中的极值点偏移问题,由于对函数f(x)的解析式求导后不好操作,并且函数f(x)的定义域为(0,+∞),f(x)的解析式中提取x后,构造新函数g(x),f(x)与g(x)有共同零点,再运用构造差函数法进行破解。

3.对数平均不等式法

两个正数a和b的对数平均值定义:

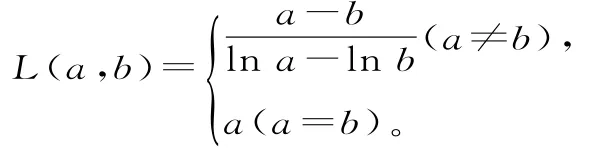
对数平均值与算术平均值、几何平均值的大小关系为:当a＞0,b＞0时,有 ab≤L(仅当a=b时,取“=”),这个不等式链叫对数平均不等式。可以利用这个不等式链破解极值点的偏移问题。

函数f(x)=m(x-1)-ln2x-1,当m＞1时,方程f(x)=0的两根为x1,x2,且x1≠x2。证明:x1+x2＞1+

证明：由题意知m(x1-1)-ln2x1-1=0。①

点评:本题属于导数中的极值点偏移问题,利用对数平均不等式可顺利解决。

从理论上来说,以上三类方法都是破解极值点偏移问题的通法,但不同题目,选取不同方法的烦琐程度不同,具体题目中选取哪一种方法,同学们要根据具体问题具体分析。