定积分的五种求法

■甘肃省白银市第一中学　胡贵平

定积分是新课标的新增内容,其中定积分的计算是重点考查的考点之一,下面通过例题来看定积分计算的五种常用方法。

一、定义法

分析：用定义法求积分可分四步:分割,以直代曲,作和,求极限。

二、基本定理法

分析：可先求出原函数,再利用微积分基本定理求解。

解：函数y=x2+2x+1的一个原函数

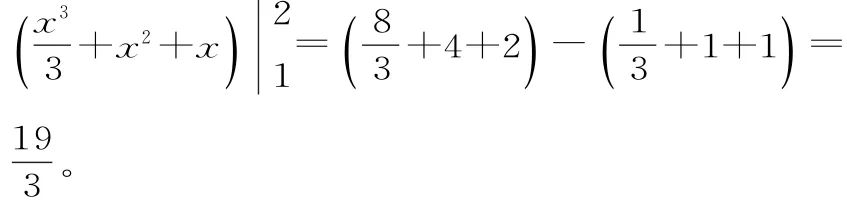
三、几何意义法

分析：利用定积分的意义是指曲边梯形的面积,只要作出图形就可求出。

图1

四、性质法

求下列定积分:

分析：对于①用微积分的基本定理可以解决,而②的原函数很难找到,几乎不能解决。若运用奇偶函数在对称区间的积分性质,则能迎刃而解。

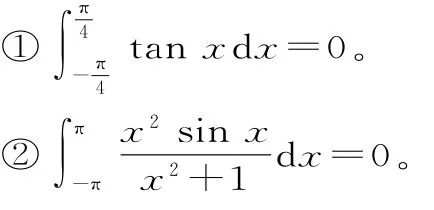
五、综合法

分析：由于积分区间关于原点对称,因此首先应考虑被积函数的奇偶性。

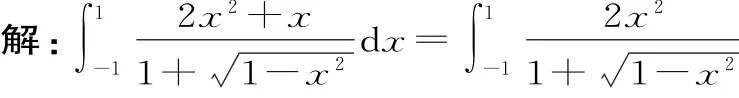
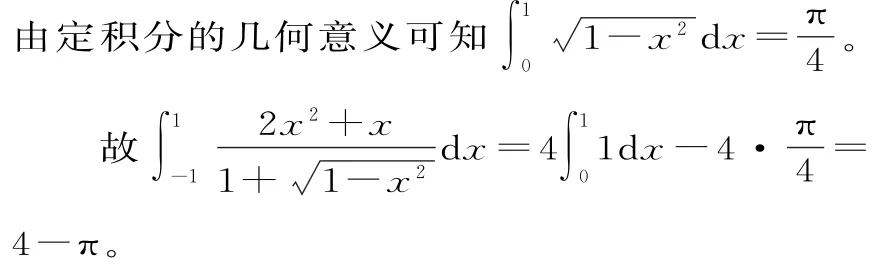
通过对这五个例题的分析,我们应该牢固记住如何求定积分的方法,懂得在什么情况下该用何种方法解决问题。