构造常数函数秒杀一类抽象函数题

■广东省深圳市盐田高级中学　丁小飞

高考或模拟考试中,在选择题中经常用抽象函数进行压轴。这样的题对函数知识、性质等要求较高,特别是构造函数和求导、利用单调性解题,给很多同学带来困扰。有很多专家对此进行了详细的研究并给出了详细的分析。但笔者近期在思考,因为是小题,有重结果不重过程之特点,能不能小题小解?于是带着这种思路去探索,试图找出简便的解答。笔者通过研究,发现有一类抽象函数题,在构造函数中,直接构造成常数函数可以快速准确解答。而这种构造简易方便,各个层次的同学都能掌握。在此以《中学数学研究》2017年第5期(上)刊登的《一道模考选择压轴题的分析与探究》的题型与变式研究来探究这种解法,以供参考。

1.原文试题、变式再现与研究

(1)原文试题:

定义在R上的函数f(x)满足:f(x)＞1且f(x)+f'(x)＞1,f(0)=5,f'(x)是f(x)的导函数,则不等式ln[f(x)-1]＞ln4-x的解集为()。

A.(0,+∞)

B.(-∞,0)∪(3,+∞)

C.(-∞,0)∪(0,+∞)

D.(-∞,0)

原文给出了详细的分析和解答:

故exf(x)-ex＞4,令h(x)=exf(x)-ex-4,则h'(x)=exf(x)+exf'(x)-ex=ex[f(x)+f'(x)-1]。

因为f(x)+f'(x)＞1,所以h'(x)=ex[f(x)+f'(x)-1]＞0。

所以h(x)单调递增,又f(0)=5,所以h(0)=e0f(0)-e0-4=0。

故h(x)=exf(x)-ex-4＞0=h(0)的解集为(0,+∞)。故答案为A。

对于此题,笔者通过研究,发现在构造函数中,直接构造成常数函数可以快速准确解答,而且构造的常数函数中的常数就是题干中给出等式中的函数值。请看笔者的妙解:

根据笔者研究的结论,可以构造函数f(x)=5,我们会发现f(x)=5满足题干中所有条件:定义在R上的函数f(x)满足:f(x)＞1且f(x)+f'(x)＞1,f(0)=5,其中f'(x)是f(x)的导函数。

于是可以用它来解题,ln[f(x)-1]＞ln4-x的解集可用构造函数来解答。

因为f(x)=5,所以ln[f(x)-1]＞ln4-x可化为ln[5-1]＞ln4-x,即ln4＞ln4-x,则0＞-x,x＞0。所以其解集为(0,+∞)。故答案为A。

由此解答既快又准,同学们也容易掌握,岂是一“妙”字了得！

也许有些读者认为是碰巧,这种方法会不会恰好只能适用于这一题。笔者尝试着解答,发现这种解法还能解答这篇文章中的变式或与变式类似的题目。

(2)原文中变式1:

定义在R上的函数f(x)满足:f(x)＞-1且2f(x)+f'(x)+2＞0,f(0)=e-1,其中f'(x)是f(x)的导函数,则不等式ln[f(x)+1]＞1-2x的解集为()。

A.(0,+∞)

B.(-∞,0)∪(3,+∞)

C.(-∞,0)∪(0,+∞)

D.(-∞,0)

笔者的妙解:

构造函数f(x)=e-1。(满足题干中所有的条件:定义在R上的函数f(x)满足:f(x)＞-1且2f(x)+f'(x)+2＞0,f(0)=e-1,其中f'(x)是f(x)的导函数)

则不等式ln[f(x)+1]＞1-2x可化为ln[e-1+1]＞1-2x,即lne＞1-2x,即0＞-2x。马上可以得出其解集为(0,+∞),答案为A。

(3)原文中变式2:

定义在R上的函数f(x)满足:f(x)＞4且3f(x)+f'(x)＜12,f(1)=4+,其中f'(x)是f(x)的导函数,则不等式ln[f(x)-4]＞2-3x的解集为()。

A.(1,+∞)

B.(-∞,1)∪(2,+∞)

C.(-∞,1)∪(1,+∞)

D.(-∞,1)

如果把小于12改成大于12,笔者的解法也是可以求解的。

新变式:定义在R上的函数f(x)满足:f(x)＞4且3f(x)+f'(x)＞12,f(1)=4+,其中f'(x)是f(x)的导函数,则不等式ln[f(x)-4]＞2-3x的解集为()。

A.(1,+∞)

B.(-∞,1)∪(2,+∞)

C.(-∞,1)∪(1,+∞)

(4)原文中变式3:

定义在R上的函数f(x)满足:f(x)＞2且4f(x)-f'(x)-8＜0,f(-)=3,其中f'(x)是f(x)的导函数,则不等式ln[f(x)-2]＞1+4x的解集为()。

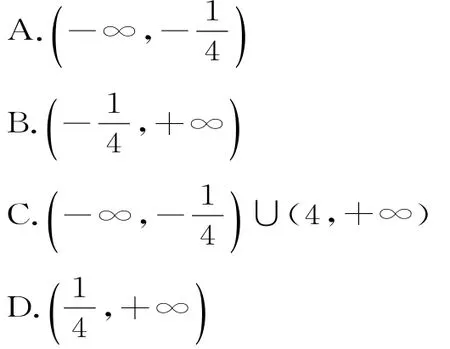
同理,如果此变式中的小于0改成大于0,运用此法也是可以求解的。

新变式:定义在R上的函数f(x)满足:f(x)＞2且4f(x)-f'(x)-8＞0,f(-)=3,f'(x)是f(x)的导函数,则不等式ln[f(x)-2]＞1+4x的解集为()。

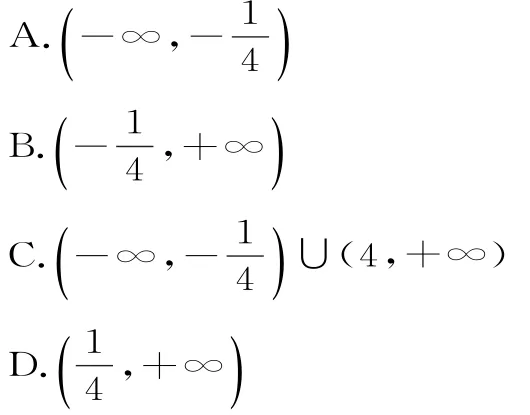
新变式的解答:构造函数f(x)=3。(满足题干中所有的条件:f(x)＞2且4f(x)-f'(x)-8＞0,f(-)=3,其中f'(x)是f(x)的导函数)

则所求的解集与ln[3-2]＞1+4x的解集相同,即0＞1+4x,解集为

是不是有秒杀之感?

这种构造其实是碰巧中有必然,何种题型可以构造呢?原文中最后“试题的解题规律”也是可应用此种解法的题型:

定义在R上的函数f(x)满足:f(x)＞-a且bf(x)-f'(x)+ab＞0,f(-)=1-a,其中f'(x)是f(x)的导函数,则不等式ln[f(x)+a]＞bx+c的解集为____。

解析：此种题型恰好能构造f(x)=1-a,满足题干中所有的条件:定义在R上的函数f(x)满足:f(x)＞-a且bf(x)-f'(x)+ab＞0,f(-)=1-a,其中f'(x)是f(x)的导函数。所以不等式ln[f(x)+a]＞bx+c的解集与不等式ln[1-a+a]＞bx+c的解集相同,与0＞bx+c的解集相同。

2.启示

数学是神奇的,里面隐藏着美妙的思维。多去思考探究,往往能有意外的惊喜,不但可以帮助我们解决“难题”,而且可以带领我们走进数学的美妙殿堂,让我们体会到数学的美。