对解析几何轨迹问题的研究

■重庆市第一中学高二(4)班　朱健坤 (指导老师:黄正卫)

轨迹方程的探求是解析几何中的基本问题之一。解答这类问题,要善于总结知识之间的相互联系。现就这类问题的解题方法和心得总结如下。

方法一：条件直译法

已知两点M(-2,0),N(2,0),点P为坐标平面内的动点,满足,求动点P的轨迹方程。

分析：题目给出了点P坐标满足的关系,直接把条件转化为坐标即可。

解：设P(x,y),由题意得:

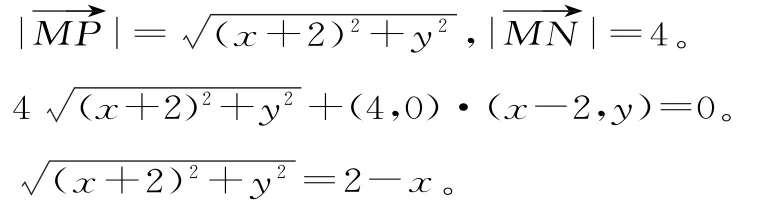
故动点P的轨迹方程为y2=-8x。

已知两定点A(-2,0),B(1,0),如果动点P满足条件|PA|=2|PB|,则点P的轨迹所包围的图形的面积等于多少?

解：由题意得,|PA|2=4|PB|2。

设P的坐标为P(x,y),则:

(x+2)2+y2=4[(x-1)2+y2]。

故(x-2)2+y2=4。

故点P的轨迹为圆,半径r=2,面积S=4π。

方法二：几何分析法(常与其他方法相联系)

如图1,已知圆M:(x+1)2+y2=8,点N(1,0),点A是圆M上任意一点,点P在直线MA上,且的轨迹方程。

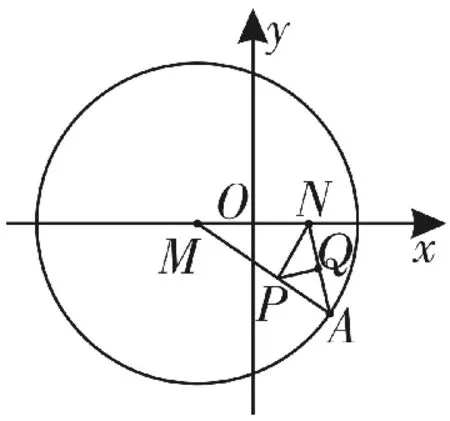
图1

解：设NA中点为Q。

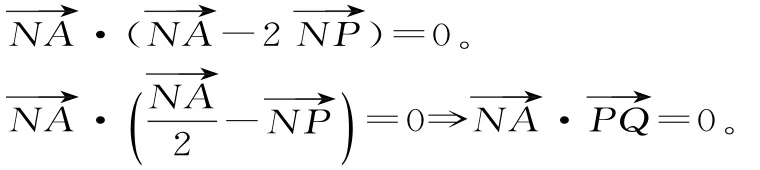
由中垂线的性质得:PA=PN。

PM+PN=MA=22＞|MN|=2。

故点P的轨迹为椭圆,a=2,c=1。

方法三：相关点法(代入法)

如果点P(x,y)的运动是随着另一点Q(x0,y0)(Q的轨迹已知或可求)运动而运动的,可用x,y把x0,y0表示出来,再代入Q的轨迹方程中,从而求得P的轨迹方程。

如图2所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,R为AB的中点,求矩形APBQ的顶点Q的轨迹方程。

解：设R(x0,y0)。

RP2=(x0-4)2+y20。RO2=x20+y20。

36=RP2+RO2。

x20+y20-4x0-10=0。

设Q(x,y),则:

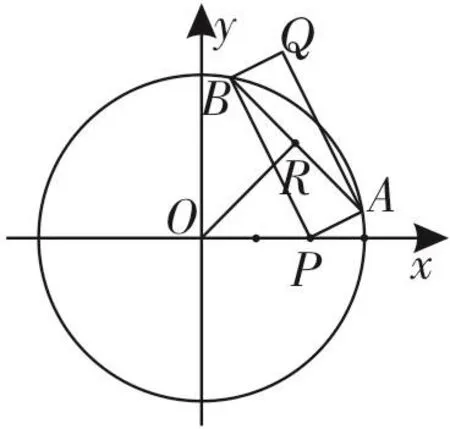
图2

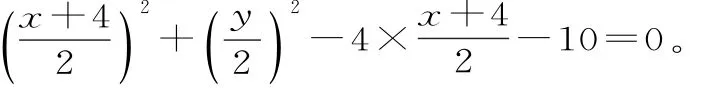
故Q的轨迹方程为x2+y2=56。

方法四：参数法

此法是选用恰当的参数(如k,θ等),分别将x,y表示出来再求解。过抛物线y2=2px的顶点O作两条互相垂直的弦OA、OB,再以OA、OB为邻边作矩形AOBM,如图3,求点M的轨迹方程。

解:如图3所示,由题意及有关知识得:

图3

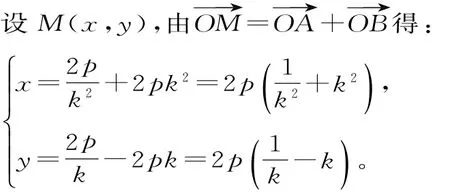
消去k得y2=2px-8p2。

故点M的轨迹方程为y2=2px-8p2。

方法五：交轨法(专门解决两动直线的交点的轨迹方程的方法)

这类问题常含双元参数,求解时常将两式相乘,然后整体代换。

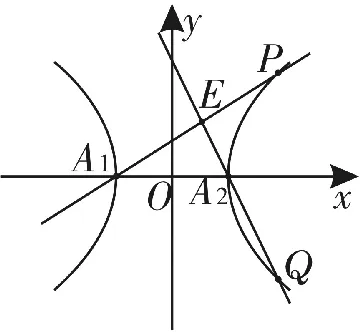
解：如图4所示。

A1(-2,0),A2(2,0)。