导数中的分类讨论问题

■河南省郑州市第七中学高三(13)班　范若聪

数学解题离不开分类讨论,导数的应用也是如此。所谓分类讨论思想,就是根据所研究对象的性质差异,分各种不同的情况予以分析解决。分类讨论题覆盖知识点较多,利于考查同学们的知识面、数学思想和解题技巧。树立分类讨论思想,应注重理解和掌握分类的原则、方法与技巧,做到“确定对象的全体,明确分类的标准,分层别类不重复、不遗漏地分析讨论”。那么,在导数问题中引起分类讨论的根源有哪些呢?下面加以分类解析,供同学们参考。

一、参数引起的分类讨论

已知函数f(x)=a(x2+1)+lnx。

(1)讨论函数f(x)的单调性;

(2)若对任意a∈(-4,-2)及x∈[1,3],恒有ma-f(x)＞a2成立,求实数m的取值范围。

综上,当a≥0时,f(x)在(0,+∞)上是增函数;

(2)由题意,知对任意a∈(-4,-2)及x∈[1,3],恒有ma-f(x)＞a2成立,等价于ma-a2＞f(x)max。

由(1)知,当a∈(-4,-2)时,f(x)在[1,3]上是减函数,所以f(x)max=f(1)=2a。

所以ma-a2＞2a,即m＜a+2。

因为a∈(-4,-2),所以-2＜a+2＜0。所以实数m的取值范围为m≤-2。

评注:由于参数a不同的取值影响到极值点是否存在,所以必须分类讨论。

二、判别式引起的分类讨论

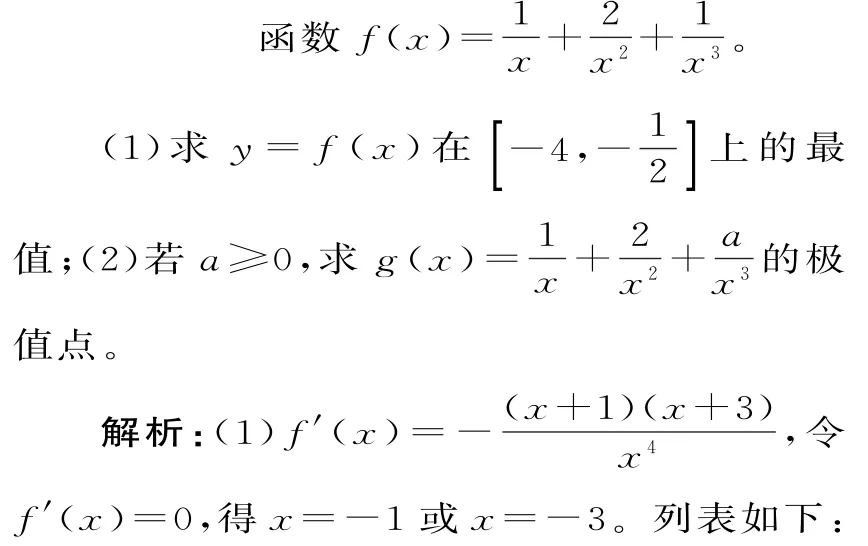
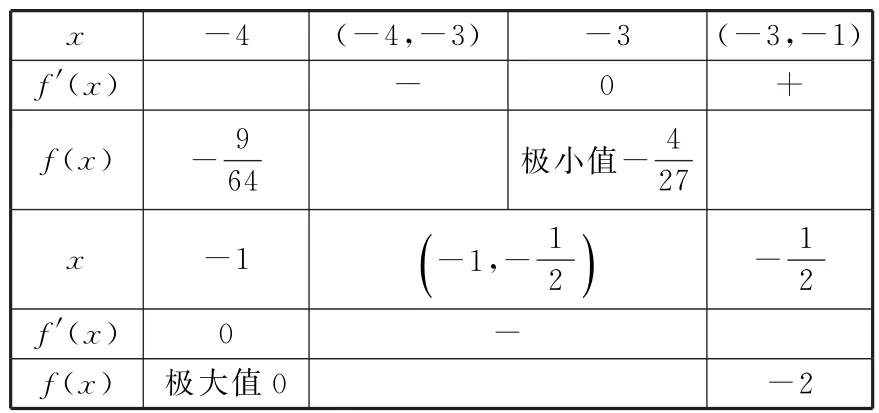
表1

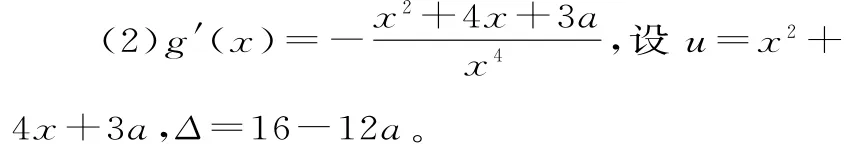
故减区间为(-∞,x1),(x2,0),增区间为(x1,x2),g(x)有两个极值点x1,x2。

故减区间为(-∞,-4),增区间为(-4,0),g(x)有一个极值点x=-4。

评注:当求极值点时涉及含参数的二次方程,必须通过对判别式Δ的讨论,来确定极值点是否存在和极值点的个数。

三、二次函数对称轴与给定区间引起的分类讨论

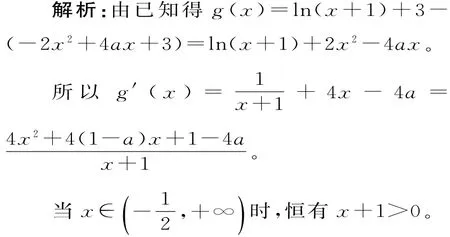
设h(x)=4x2+4(1-a)x+1-4a,其对称轴为

综上知,实数a的取值范围是a≤0。

评注:当把导数的单调性问题转化为含参二次函数恒大于零或恒小于零问题时,往往要通过讨论二次函数的对称轴的位置来确定二次函数的值在定义域内的正负。

四、极值点与给定区间引起的分类讨论

已知函数f(x)=(4x2+4ax+a2)x,其中a＜0。

(1)当a=-4时,求f(x)的单调递增区间;

(2)若f(x)在区间[1,4]上的最小值为8,求a的值。

综上有a=-10。

评注:由于极值点是否在给定的区间上,直接制约着函数在给定区间上的单调性,所以必须对极值点是否在给定的区间上进行分类讨论。

五、单调性不确定引起的分类讨论

(2)若函数f(x)在[-1,1]上为单调函数,求实数a的取值范围。

令f'(x)=0,得ex=1或ex=2,即x=0或x=ln2。

令f'(x)＞0,则x＜0或x＞ln2;令f'(x)＜0,则0＜x＜ln2。

所以f(x)的增区间是(-∞,0],[ln2,+∞),减区间是(0,ln2)。

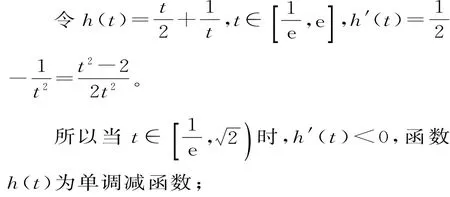
当t∈(2,e]时,h'(t)＞0,函数h(t)为单调增函数。

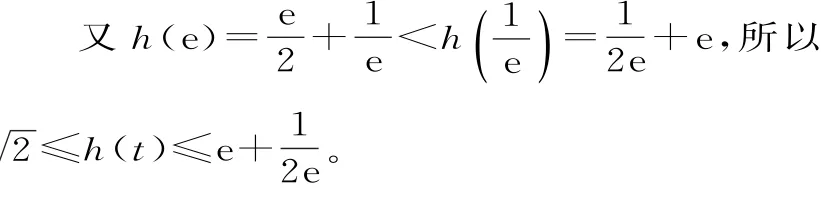
由于函数f(x)在[-1,1]上为单调函数,则:

评注:第(2)小题没有明确函数f(x)在[-1,1]上为单调增函数还是单调减函数,故需分类讨论。解答本题的关键是利用导数与单调性的关系将问题转化为不等式的恒成立问题,进而通过分离参数将不等式的恒成立问题转化为求函数的最值问题来处理。

本文最后提醒大家,在新课标高考数学命题中,对函数与导数的考查往往以综合题的形式出现在压轴题中,试题中的函数往往含有参数,这类试题不仅仅考查函数与导数的相关知识,更是考查分类讨论思想的灵活运用,望能引起同学们的高度重视。