一道数列题求通项的思考探究

■浙江省天台中学高二(15)班　何秉烜(指导教师:徐 凤)

有一类数列试题,是需要求通项公式的,课本只是在作业里提了一下,意思是不作高要求。其实,高考中这类题十分重要,经常考到。如2014年高考数学全国新课标Ⅱ卷理科第17题就是一道数列与不等式的常规题,该题主要考查等比数列的定义、数列通项公式的求解以及数列中不等式的证明等基础知识。原题如下:

原题 已知数列an{}满足a1=1,an+1=3an+1。

证明{an+}是等比数列,并求{an}的通项公式。

下面进行探究。

证法1：(构造法) 由an+1=3an+1得

证法3：(归纳猜想法)由已知得:

……

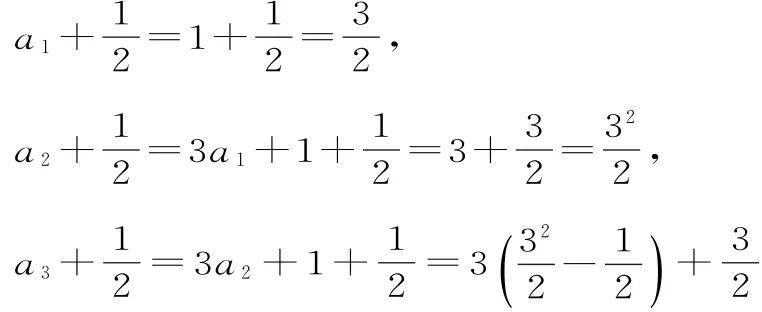
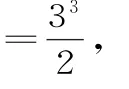
这里的证明用数学归纳法就行。

评析：上述证法1是参考答案提供的原证法,这种证法的第一步“由an+1=3an+1是利用“添项法”完成的,对一般同学来说,通常会遇到两个问题:一是为什么要添项?二是添什么项?这两个问题容易导致有些同学思维障碍的形成。虽然在平时的数学学习中,老师也讲过这种类型的递推数列通项公式的求法,但是,因为有些同学对这两个问题较难理解,再加上这种“添项法”又具有一定的技巧性,所以这种证法很多同学容易出错。证法2则紧扣等比数列的定义,按照求路,利用“代入法”,将条件“an+1=3an+1”代3”变得自然、优美,而且贴近我们的思维。因此,证法2优于证法1。证法3从求数列{an+}的通项公式入手,首先想到了归纳猜想法,这种方法是一种习惯性的常规思维,符合多数同学的实际,虽然过程复杂了一些,但却是可行和有效的。

二、关于an{　}的通项公式的求法

原题将“求{an}的通项公式”放到了“证明{an+}是等比数列”之后,这里边明显存在着一种暗示,就是先求{an+}的通项公式,然后从中可以得出{an}的通项公式,于是就有:

受证法1的启发,可得:

解法2：由an+1=3an+1得2an+1=6an+2,两边同时加上1,得:

2an+1+1=6an+3=3(2an+1)。

所以{2an+1}是首项为2a1+1=3,公比为3的等比数列,于是得2an+1=3×3n-1,整理得

解法3:由已知得:

a1=1,

a2=3a1+1=3+1,

a3=3a2+1=32+3+1,

……

猜想:an=3n-1+3n-2+…+32+3+1。②

将②式右边求解,得:

评析：将上述证法3和解法3这两种归纳猜想法比较可以发现,前者通过归纳猜想法得到①式很容易,但是后者如果将前3项写成:a1=1,a2=4,a3=13,那么就发现不了各项之间的规律,使归纳猜想法陷入困境。相反,解法3正是注意到了这一危险境地,巧妙地避险排难,采取将前3项中的各个加法项搁置起来,使各项之间的规律性得以充分彰显,从而让②式顺利浮出水面。