聚焦导数压轴试题 破译高考命题密码

■广东省兴宁市第一中学　蓝云波

导数是高中数学的重要内容,在高考中通常占据压轴题的位置,其重要性不言而喻。通过对近几年全国卷导数压轴题的分析,可发现函数与导数压轴题综合性强,方法多样,技巧性强,难度颇大。这类试题题型多样,常考常新,但解题的关键在于数学思想方法的合理使用。为帮助同学们突破此类问题,下面从四个视角研究导数压轴题的破解策略,以提高同学们的解题能力。

一、函数的单调性、最值

(河北省衡水中学2017届高三上学期期中考试理科)已知函数f(x)=alnx+x2(a为实常数)。

(1)若a=-2,求证:函数f(x)在(1,+∞)上是增函数;

(2)求函数f(x)在[1,e]上的最小值及相应的x值;

(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围。

若a≥-2,则f'(x)在[1,e]上非负(仅当a=-2,x=1时,f'(x)=0),故函数f(x)在[1,e]上是增函数,此时f(x)min=f(1)=1。

f(x)min=

若a≤-2e2,f'(x)在[1,e]上非正(仅当a=-2e2,x=e时,f'(x)=0),故函数f(x)在[1,e]上是减函数,此时f(x)min=f(e)=a+e2。

综上可知,当a≥-2时,f(x)的最小值为1,相应的x值为1;

当a≤-2e2时,f(x)的最小值为a+e2,相应的x值为e。

(3)不等式f(x)≤(a+2)x,可化为a(x-lnx)≥x2-2x。

因为x∈[1,e],所以lnx≤1≤x且等号不能同时取,即lnx＜x,故x-lnx＞0。

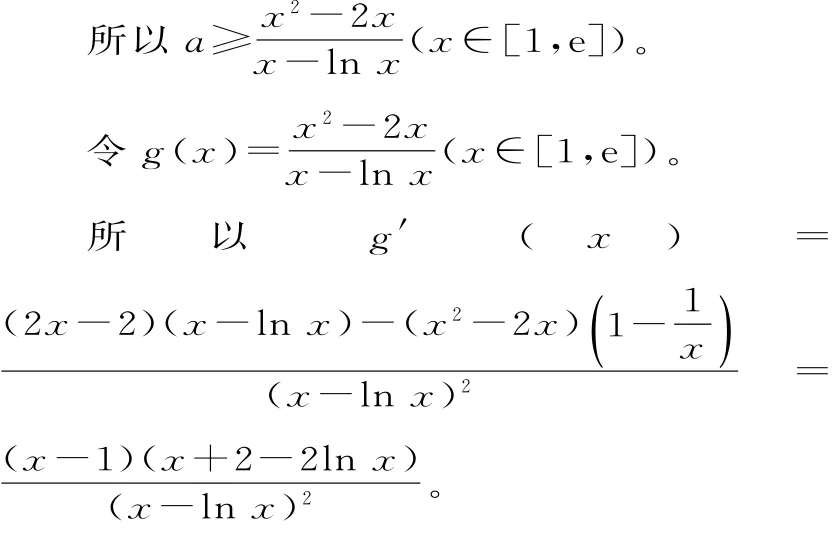
当x∈[1,e]时,x-1≥0,lnx≤1,故x+2-2lnx＞0,从而g'(x)≥0(仅当x=1时取等号),所以g(x)在[1,e]上为增函数。

故g(x)的最小值为g(1)=-1,所以a的取值范围是[-1,+∞)。

点评:求解含参数的函数最值问题,关键是对参数进行分类讨论。对于第三问的能成立问题,则是通过分离参数,转化为新的函数的最小值求解。在解题中,特别要注意恒成立问题与能成立问题的区别。

(湖南省岳阳市2017届高三联考理科改编)已知函数f(x)=ln(x+1)-

(1)当a=1时,求函数f(x)在x=e-1处的切线方程;

所以当a=1时,函数f(x)在x=e-1处的切线的斜率为

此时f(x)在(-1,0),(2a-3,+∞)上单调递增,在(0,2a-3)上单调递减。

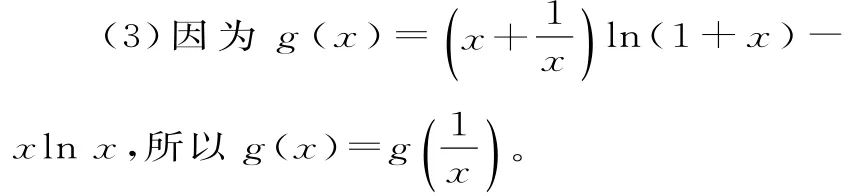
因此g(x)在(0,+∞)上的最大值等于其在(0,1]上的最大值。

由(2)知,当a=2时,f(x)在区间(0,1]上单调递减,所以f(x)=ln(1+x)-h(x)在区间(0,1]上单调递减,于是h(x)≥h(1)=0。

从而函数g(x)在区间(0,1]上单调递增,进而g(x)≤g(1)=2ln2,即g(x)的最大值为ln4。

点评:本题通过对函数g(x)的细致观察,发现g(x)=g(),从而把研究问题的范围缩小,实现了化难为易的效果。在求最值的过程中,还使用了二次求导的技巧。

二、函数的零点问题

(1)讨论函数f(x)的单调性;

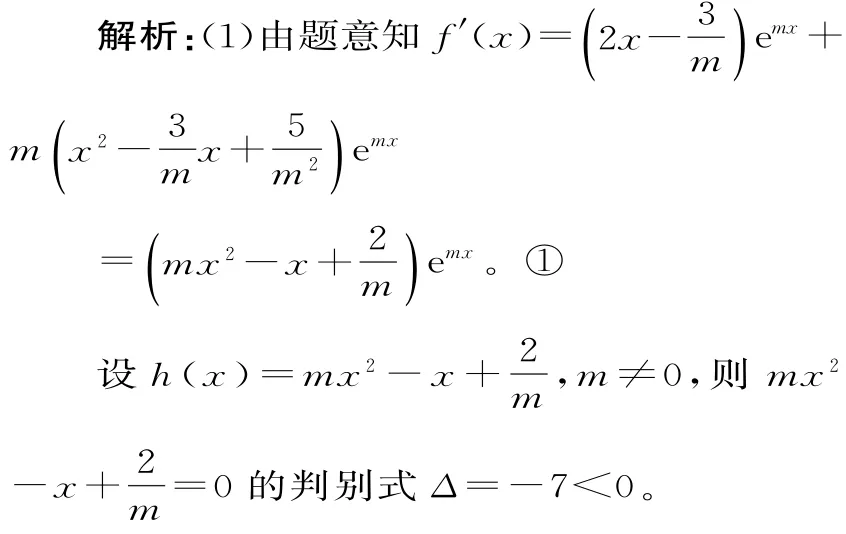
因此,当m＜0时,h(x)＜0,可得f'(x)＜0,此时f(x)在(-∞,+∞)上单调递减;

当m＞0时,h(x)＞0,可得f'(x)＞0,此时f(x)在(-∞,+∞)上单调递增。

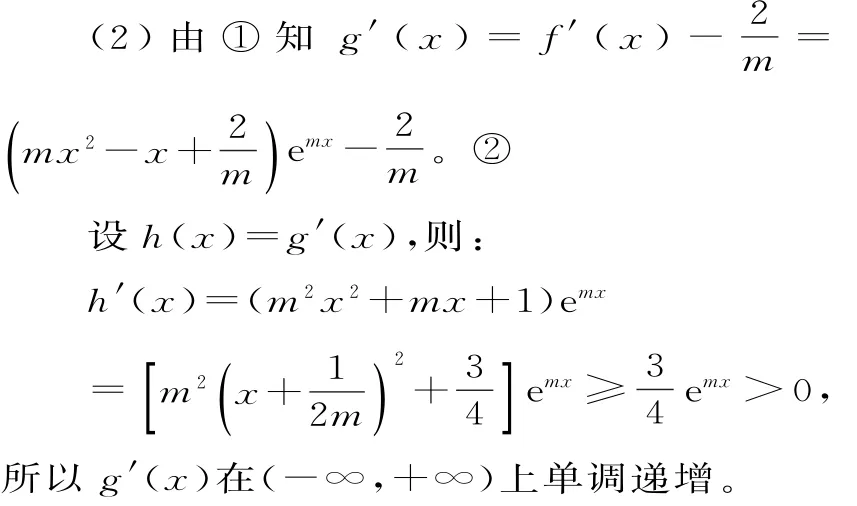
由②得g'(0)=0,所以当x＜0时,g'(x)＜g'(0)=0,g(x)在(-∞,0)上单调递减;当x＞0时,g'(x)＞g'(0)=0,g(x)在(0,+∞)上单调递增。

又g(0)＜0,g(x)在(-∞,0)上单调递减,故g(x)在(-∞,0)上恰有一个零点。

另一方面,当x＞0时,emx＞1。

又g(0)＜0,g(x)在(0,+∞)上单调递增,故g(x)在(0,+∞)上恰有一个零点。

从而当m＞1时,g(x)恰有两个零点。

同理可证当m＜-1时,g(x)恰有两个零点。

综上可知,满足题意的m的取值范围是(-∞,-1)∪(1,+∞)。

(贵阳市2017届高三上学期期末测试卷)已知函数f(x)=2a2lnx-x2(a＞0)。

(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;

(2)求函数y=f(x)的单调区间;

(3)讨论函数y=f(x)在区间(1,e2)上零点的个数。

又因为f(1)=2ln1-12=-1,所以曲线y=f(x)在点(1,f(1))处的切线方程为y=-1。

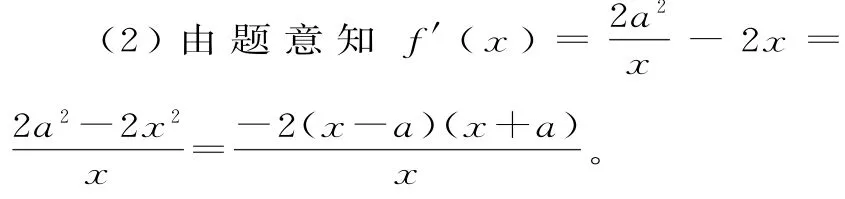
因为x＞0,a＞0,所以当0＜x＜a时,f'(x)＞0;当x＞a时,f'(x)＜0。

因此,f(x)在(0,a)上是增函数,在(a,+∞)上是减函数。

(3)由(2)得:

f(x)max=f(a)=a2(2lna-1)。

下面讨论函数f(x)的零点情况。

①当a2(2lna-1)＜0,即0＜a＜e时,函数f(x)在(1,e2)上无零点。

②当a2(2lna-1)=0,即a=e时,函数f(x)在(0,+∞)内有唯一零点a,又1＜a=e＜e2,故函数f(x)在(1,e2)内有一个零点。

③当a2(2lna-1)＞0,即a＞e时,由题意知f(1)=-1＜0,f(a)=a2(2lna-1)＞0,f(e2)=2a2lne2-e4=4a2-e4=(2ae2)(2a+e2)。故当2a-e2＜0,即 e＜a＜时,1＜e＜a＜＜e2,f(e2)＜0,由单调性可知,函数f(x)在(1,a)内有唯一零点x1,在(a,e2)内有唯一零点x2,所以f(x)在(1,e2)内有两个零点。

当2a-e2≥0,即a≥＞e时,f(e2)≥0,而且f(e)=2a2·-e=a2-e＞0,f(1)=-1＜0,由单调性可知,无论a≥e2还是a＜e2,f(x)在(1,e)内有唯一的一个零点,在(e,e2)内没有零点,从而f(x)在(1,e2)内只有一个零点。

综上所述,当0＜a＜e时,函数f(x)无零点;当a=e或a≥,函数f(x)有一个零点;当 e＜a＜,函数f(x)有两个零点。

例3和例4是函数零点问题,运用数形结合思想是关键。在研究函数时,二次求导是常见的策略。函数零点个数的确定,往往要借助零点存在定理,使用零点存在定理的难点在于利用单调性后,区间内两个函数值的乘积小于零的确定,往往要结合放缩法以确定函数值的符号。

三、证明不等式

(2016年广州市一模理科数学卷)已知函数f(x)=ex+m-x3,g(x)=ln(x+1)+2。

(1)若曲线y=f(x)在点(0,f(0))处的切线斜率为1,求实数m的值;

(2)当m≥1时,请证明:f(x)＞g(x)-x3。

解析：(1)因为f'(x)=ex+m-3x2,所以f'(0)=em-3×02=1,解得m=0。

(2)f(x)＞g(x)-x3等价于ex+mln(x+1)-2＞0。

当m≥1时,ex+m-ln(x+1)-2≥ex+1-ln(x+1)-2。

所以要证ex+m-ln(x+1)-2＞0,只需证明ex+1-ln(x+1)-2＞0。

设h(x)=ex+1-ln(x+1)-2。

当x∈(-1,x0)时,h'(x)＜0;

当x∈(x0,+∞)时,h'(x)＞0。

故当x=x0时,h(x)取得最小值h(x0)。

所以h(x)≥h(x0)=ex0+1-ln(x0+1)

综上所述,当m≥1时,f(x)＞g(x)-x3成立。

解析：由题意可知f(x)的定义域为(0,+∞)。

令F'(x)＞0,得0＜x＜1;

令F'(x)＜0,得x＞1。

所以F(x)的增区间为(0,1),减区间为(1,+∞)。

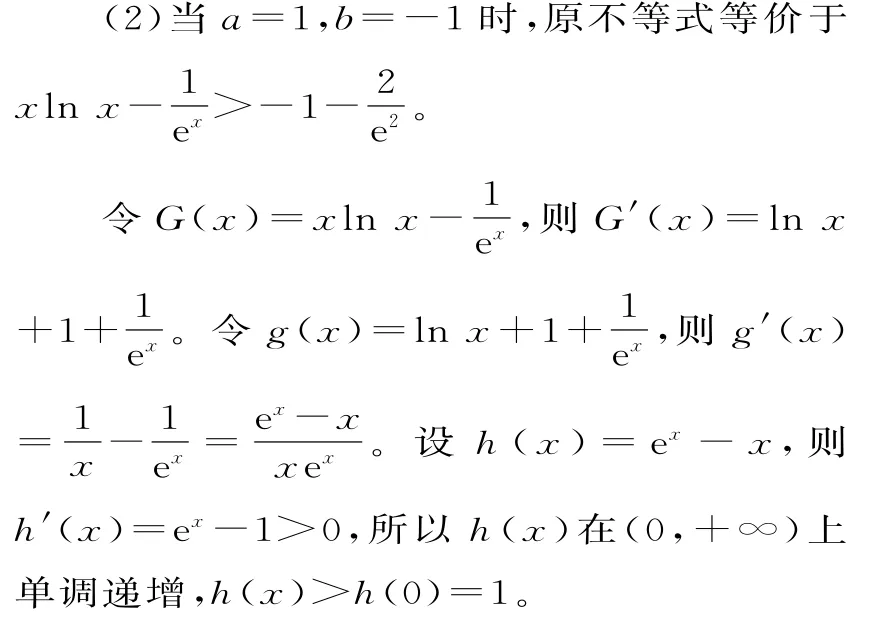
所以g'(x)＞0,g(x)在(0,+∞)上单调递增。

当x∈(0,x0)时,g(x)＜0,G(x)单调递减;当x∈(x0,+∞)时,g(x)＞0,G(x)单调递增。所以G(x)≥G(x0)=x0lnx0-e-x0=x0lnx0+lnx0+1。

G(x)≥G(x0)=φ(x0)＞-1-2e-2。

例5和例6是高考中利用导数证明不等式的热点问题,常见的做法是构造函数,通过函数的最值进行证明。试题通过作差构造函数,并通过多次求导,以确定函数的最值,但由于函数的极值点难以求解,故可借助设而不求,整体代换的技巧实现问题的解决。构造函数,借助导数证明不等式,除直接作差构造之外,还可通过下列技巧求解:

①分离参数后构造函数;

②通过代数变形(如取对数)后构造函数;

③换元构造,声东击西;

④构造双函数,各个击破;

⑤主元构造,定主略从;

⑥放缩构造,化繁为简;

⑦多次构造,多次求导。

四、极值点偏移问题

(2016年甘肃省兰州市高三诊断考试)已知函数f(x)=ex-ax-1(a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为-1。

(1)求a的值及函数y=f(x)的单调区间;

(2)若x1＜ln2,x2＞ln2,且f(x1)=f(x2),试证明:x1+x2＜2ln2。

解析：(1)因为f'(x)=ex-a,又f'(0)=1-a=-1,所以a=2。

故f(x)=ex-2x-1,f'(x)=ex-2。

由f'(x)＞0,得x＞ln2;由f'(x)＜0,得x＜ln2。

所以函数y=f(x)在(-∞,ln2)上单调递减,在(ln2,+∞)上单调递增。

(2)设x＞ln2,所以2ln2-x＜ln2,f(2ln2-x)=e(2ln2-x)-2(2ln2-x)-1=

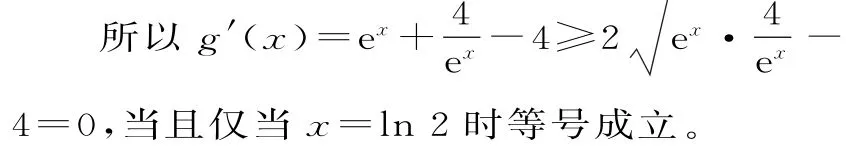
所以g(x)在(ln2,+∞)上单调递增。

又因为g(ln2)=0,所以当x＞ln2时,g(x)=f(x)-f(2ln2-x)＞g(ln2)=0。故f(x)＞f(2ln2-x)。

因此,f(x2)＞f(2ln2-x2)。

又因为f(x1)=f(x2),所以f(x1)＞f(2ln2-x2)。

由于x2＞ln2,所以2ln2-x2＜ln2,又因为x1＜ln2,由(1)知函数y=f(x)在(-∞,ln2)上单调递减,所以x1＜2ln2-x2。

因此,x1+x2＜2ln2,得证。

(1)讨论f(x)的单调性。

(2)设a＞0,证明:当0＜x＜a时,f(a+x)＜f(a-x)。

(3)设x1,x2是f(x)的两个零点,证明

解析：(1)由题意可知f(x)的定义域为(0,+∞)。

①若a≤0,则f'(x)＞0,此时f(x)在(0,+∞)上单调递增;

②若a＞0,则由f'(x)=0得x=a,当0＜x＜a时,f'(x)＜0,当x＞a时,f'(x)＞0,此时f(x)在(0,a)上单调递减,在(a,+∞)上单调递增。

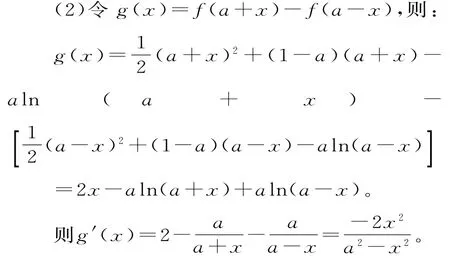
当0＜x＜a时,g'(x)＜0,所以g(x)在(0,a)上是减函数。

而g(0)=0,所以g(x)＜g(0)=0,故当0＜x＜a时,f(a+x)＜f(a-x)。

(3)由(1)可知,当a≤0时,函数y=f(x)至多有一个零点,故a＞0,从而f(x)的最小值为f(a),且f(a)＜0。

不妨设0＜x1＜x2,则0＜x1＜a＜x2,所以0＜a-x1＜a。

由(2)得f(2a-x1)=f(a+a-x1)＜f(x1)=f(x2)=0。

例7和例8是经典的极值点偏移问题,所谓极值点偏移问题,就是:已知函数y=f(x)是连续函数,f(x)在区间(x1,x2)内只有一个极值点x0,且f(x1)=f(x2),不少极值函数由于极值点左右的增减速度不同,函数图像不具对称性,常常有极值点x0≠的情况。解决这类问题首先应确定零点的大致范围,从所证结论出发,构造差函数,结合函数的单调性与等量代换,实现问题的解决。