导数的应用创新题直击

■郑州外国语学校高三(15)班　银子麒

■郑州外国语学校高三(15)班银子麒

导数,一向被认为是研究函数问题的“神器”,有些问题看似与导数无关,其实必须依赖导数才可以解决。让我们一起来直击几例导数的应用创新题吧。

一、函数的零点问题

A.0B.1C.2D.3

解析：求导得f'(x)=1-x+x2-x3+…+x2016,可知当x=-1时,f'(x)＞0。

点评:本题具有一定的综合性,对能力的要求较高,解题关键是灵活利用“分类与整合思想”准确分析导数与零的大小关系。

二、不等式的解集问题

(1)函数的定义域为R,f(-1)=2,对任意x∈R,f'(x)＞2,则f(x)＞2x+4的解集为()。

A.(-1,1) B.(-1,+∞)

C.(-∞,-1)D.(-∞,+∞)

(2)已知函数f(x)满足f(1)=1,导函数f'(x)＜,则不等式2f(x)＜x+1的解集为()。

A.(-1,1)

B.(-∞,-1)

C.(1,+∞)

D.(-∞,-1)∪(1,+∞)

解析：(1)构造函数F(x)=f(x)-2x-4,则F'(x)=f'(x)-2＞2-2=0,所以F(x)在R上单调递增,又因为F(-1)=f(-1)-2·(-1)-4=0,则f(x)＞2x+4⇔f(x)-2x-4＞0⇔F(x)＞0,于是得x＞-1,选B。

(2)构造函数F(x)=2f(x)-x-1,则F'(x)=2f'(x)-1＜2·-1=0,所以函数F(x)单调递减,而F(1)=0,2f(x)＜x+1等价于F(x)＜0,得x＞1,选C。

点评:合理构造函数,并利用导数确定函数的单调性,是破解这类问题的关键,也是难点所在。这类问题能较好地考查我们分析问题和解决问题的能力。

三、函数值的大小比较问题

(1)f(x)在R上的导函数为f'(x),且f'(x)＞f(x),且a＞0,则下面的不等式成立的有()。

A.f(a)＞eaf(0)B.f(a)＜eaf(0)

C.f(a)＞f(0)D.f(a)＜f(0)

(2)函数f(x)的导函数为f'(x),若对任意的实数x,都有2f'(x)＞f(x)成立,则3f(2ln2)与2f(2ln3)的大小关系为。

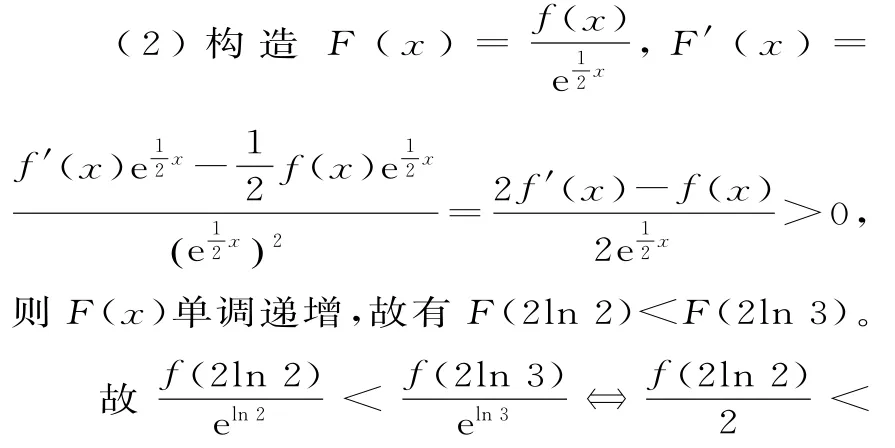
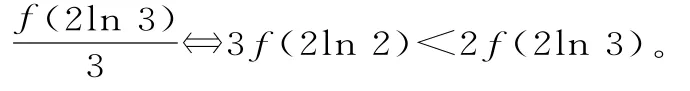
点评:抽象函数的函数值的大小比较,一般依据函数的单调性。因此解决此类问题的关键还是构造函数,并利用导数确定该函数的单调性。