导数测试题B 卷参考答案

一、选择题

1.C 2.C 3.B 4.B 5.D 6.A

7.D 8.D 9.D 1 0.A 1 1.B 1 2.C

二、填空题

三、解答题

17.(1)因为s=8-3t2,所以 Δs=8-3(1+Δt)2-(8-3×12)=-6 Δt-3(Δt)2,所以质点在[1,1+Δt]这段时间内的平均速度为

(2)定义法:质点在t=1时的瞬时速度为

求导法:质点在t时刻的瞬时速度v=s'(t)=(8-3t2)'=-6t,所以当t=1时,v=-6×1=-6。

可得当0＜x＜1时,f'(x)＜0,当x＞1时,f'(x)＞0。

所以f(x)在(0,1)上递减,在(1,+∞)上递增,所以f(x)的最小值为f(1)=1。

当n=1时,a1=0,ln(n+1)-lnn=ln2,所以

当a=1时,f'(x)≥0,函数f(x)在(-∞,+∞)上单调递增。

当a＜1时,函数f(x)在(-∞,a),(1,+∞)上单调递增,在(a,1)上单调递减。

当a＞1时,函数f(x)在(a,+∞)上单调递增,在(1,a)上单调递减。

(2)要证∀x∈[0,+∞),f(x)≥-1,即证x∈[0,+∞),f(x)min≥-1。

①由(1)可知,当a＞1,x∈[0,+∞)时,f(x)min=m i n{f(0),f(a)}。f(0)=-1,

②当a=1时,函数f(x)在[0,+∞)上单调递增,f(x)min=f(0)=-1。

③当3-e≤a＜1时,由(1)可知,x∈[0,+∞)时,f(x)min=m i n{f(0),f(1)}。

综上,当a≥3-e时,∀x∈[0,+∞),f(x)≥-1。

(2)欲证x-6≤f(x)≤x,只需证-6≤f(x)-x≤0。

(3)由(2)可得,F(x)=|f(x)-(x+a)|=|f(x)-x-a|=|g(x)-a|。

因为在[-2,4]上,-6≤g(x)≤0,令t=g(x),h(t)=|t-a|,则问题转化为:当t∈[-6,0]时,求h(t)的最大值M(a)的问题了。画出函数h(t)的图像,如图1所示。

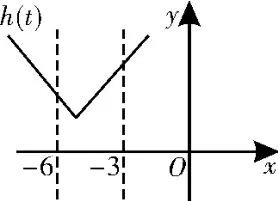
图1

①当a≤-3时,M(a)=h(0)=|a|=-a,此时-a≥3,当a=-3时,M(a)取得最小值3;

②当a≥-3时,M(a)=h(-6)=|-6-a|=|6+a|,因为6+a≥3,所以M(a)=6+a,即当a=-3时,M(a)的最小值为3。

综上,当M(a)取最小值时a的值为-3。