五种方法巧解函数零点问题

■河南省太康县第一高级中学

例题已知函数f(x)=a x3-3x2+1,若f(x)存在两个零点,则a的值为( )。

A.2或0 B.-2或0

C.0 D.±2或0

考查意图：本题主要考查函数与方程思想、数形结合思想、等价转化思想。将函数零点、方程的解等知识结合在一起,考查同学们的运算能力、动手作图能力及观察能力。

解法1：直接法。

当a=0时,f(x)=-3x2+1,恰有两个零点。

当a≠0时,f'(x)=3a x2-6x,令f'(x)=0,得x=0或

(1)若a＞0,当x∈(-∞,0)时,f'(x)＞0;当时,f'(x)＜0;当x∈时,f'(x)＞0。所以函数f(x)在(-∞,0)和上单调递增,在上单调递减,且f(0)=1＞0,故f(x)有1个小于零的零点,只需令,即a2=4,解得a=2。

(2)若a＜0,当时,f'(x)＜0;当时,f'(x)＞0;当x∈(0,和(0,+∞)上单调递减,在+∞)时,f'(x)＜0。所以函数f(x)在上单调递增,且f(0)=1＞0,故f(x)有1个大于零的零点,只需令,即a2=4,解得a=-2。

综上可知,a=±2或0。

解法2：转化为直线与曲线的交点问题。

由a x3-3x2+1=0可知x≠0,所以,作出的图像,如图1所示,转动直线y=a x,显然a=0时成立。

图1

当a＜0,直线y=a x与左边的曲线相切时,设切点为,其中t＜0,则切线方程为又切线过原点,则有,解得t=-1或t=1,此时切线的斜率为-2或2。

综上可知,a=±2或a=0。

解法3：转化为两曲线的交点问题。

令f(x)=0,得a x3=3x2-1。

问题转化为g(x)=a x3的图像与h(x)=3x2-1的图像存在两个交点。

当a=0时,函数g(x)的图像与h(x)的图像存在两个的交点。

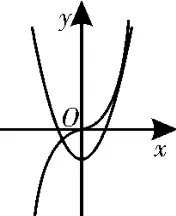
图2

当a＞0时,如图2所示,可先求出函数g(x)=a x3与h(x)=3x2-1的图像有公切线时a的值。由g'(x)=h'(x),g(x)=h(x),得a=2。由图形可知,当a=2时,满足题意。

当a＜0时,如图3所示,可先求出函数g(x)=a x3与h(x)=3x2-1的图像有公切线时a的值。由g'(x)=h'(x),g(x)=h(x),得a=-2。由图形可知,当a=-2时,满足题意。

综上可知,a=±2或a=0。

解法4：分离参数。

易知x≠0,令f(x)=0,则

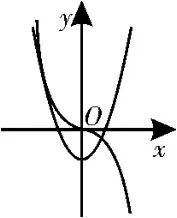
图3

可知g(x)在(-∞,-1)和(1,+∞)上单调递减,在(-1,0)和(0,1)上单调递增,且g(-1)=-2,g(1)=2,画出函数g(x)的图像,如图4所示,平移直线y=a,结合图像,可知a=±2或a=0。

在输送臂的运动过程中，可以实时观察到变量的变化情况，对于发现问题及时对参数或者函数进行修改，直到合理为止。试验证明，利用ADAMS技术建立输送臂的虚拟样机，并进行运动仿真，大大提高了生产率，为输送臂的控制提供了有力依据。

图4

解法5：特例法。

取a=2,则f(x)=2x3-3x2+1。由于f(0)=1,f(-1)＜0,从而f(x)在(-∞,0)上存在零点,又f(1)=0,所以排除B、C。

取a=-2,则f(x)=-2x3-3x2+1。由于f(0)=1,f(1)＜0,从而f(x)在(0,+∞)上存在零点,又f(-1)=0,所以排除A。故选D。

复习建议：函数零点的求解与判断方法包括:

(1)直接求零点:令f(x)=0,如果能求出解,则有几个解就有几个零点。

(2)零点存在性定理:利用定理不仅需要函数在区间[a,b]上是连续不断的曲线,且f(a)·f(b)＜0,还必须结合函数的图像与性质(如单调性、奇偶性)才能确定函数有多少个零点。

(3)分离参数法:先将参数分离,转化成求函数值域问题再加以解决。

(4)利用图像交点的个数:将函数变形为两个函数的差,画出两个函数的图像,看其交点的横坐标有几个不同的值,就有几个不同的零点。

(5)特殊值法:取选项中的特殊值代入验证,逐个排除,最终找出正确答案。

1.已知当x∈[0,1]时,函数y=(m x-1)2的图像与y=x+m的图像有且只有一个交点,则正实数m的取值范围是( )。

解析：当1)2单调递减,且y=(m x-1)2∈[(m-1)2,单调递增,且[m,1+m],此时有且仅有一个交点;

当m＞1时在上单调递增,所以要有且仅有一个交点,需(m-1)2≥1+m⇒m≥3。故选B。

解析：由题意可知,问题等价于方程x3=b(x≤a)与方程x2=b(x＞a)的根的个数和为2。

若两个方程各有一个根,则可知关于b的不等式组有解,所以a2＜b＜a3,从而a＞1;

若方程x3=b(x≤a)无解,方程x2=b(x＞a)有两个根,则可知关于b的不等式有解,从而 。a＜0

综上,实数a的取值范围是(-∞,0)∪(1,+∞)。