微积分创新题例析
■河南省太康县第一高级中学
本专题在近五年的全国卷中未考查,但却是自主命题地区的命题热点,常考查定积分的求解及定积分的应用,多以选择题、填空题的形式出现,属于中低档题,其试题难度相对较小,重点考查定积分的几何意义、基本性质和微积分基本定理。
类型一、利用微积分基本定理求定积分
例1

考点:定积分的应用。
解析:由题意得故选A。
点评:一个函数的导函数是唯一的,而其原函数则有无穷多个,这些原函数之间都相差一个常数,在利用微积分基本定理求定积分时,只要找到被积函数的一个原函数即可,并且一般使用不含常数的原函数,这样有利于计算,微积分基本定理也是求定积分最基本的方法。
类型二、巧选积分变量求定积分
例2求抛物线y2=2x与直线y=x-4围成的平面图形的面积。

图1
解析:如图1,解方程组得直线与抛物线的交点为(2,-2),(8,4)。
方法一:选取横坐标x为积分变量,则图中阴影部分的面积应该是两部分之和,即S
方法二:选取纵坐标y为积分变量,则图中阴影部分的面积可按公式求得,即S
点评:从上述两种解法可以看出,对y积分比对x积分计算要简捷。因此,应用定积分求平面图形面积时,积分变量的选取是至关重要的。但同时也要注意对y积分时,积分函数应是x=φ(y),本题需将条件中的曲线方程、直线方程化为和x=y+4的形式,然后求得积分。另外还要注意的是对面积而言,不管选用哪种积分变量去积分,面积是不会变的,即定积分的值不会改变。
类型三、巧用对称性求定积分
例3 求由三条曲线y=x2,4y=x2,y=1所围图形的面积。

图2
解析:如图2,因为y=x2,4y=x2是偶函数,根据对称性,只算出y轴右边的图形的面积再两倍即可。
方法一:选择x为积分变量,则S=2·
方法二:可以选择y为积分变量,则
点评:利用函数的奇偶性及所对应曲线的对称性解题,也是简化计算过程的常用手段,对称性的应用和积分变量的选取都影响着计算过程的繁简程度。
类型四、分割计算求定积分
例4 求由抛物线y=-x2+4x-3及其在点M(0,-3)和N(3,0)处的两条切线所围成的图形的面积。
解析:由y=-x2+4x-3,得y'=-2x+4,所以y'|x=0=4,过M点的切线方程为y=4x-3;y'|x=3=-2,过N点的切线方程为y=-2x+6。
又可求得两切线交点的横坐标为x=,故所求面积
点评:本题求图形的面积,适当的分割是关键,求出两切线交点,过交点作x轴垂线,将图形分割成两部分,分别用定积分求解。同学们应注意掌握这种分割的处理方法。
跟踪训练:
解析:因为,所以,所以a=1。
2.在同一坐标系中作出曲线x y=1、直线y=x及直线y=3的图像,如图3所示,则曲线x y=1与直线y=x和y=3所围成的平面图形的面积为____。
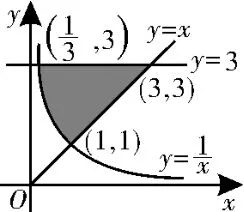
图3
解法一:选取横坐标x为积分变量,则图中阴影部分的面积应该是两部分之和,即所求区域面积
解法二:选取纵坐标y为积分变量,则图中阴影部分的面积可按公式求得,即所求区域面积
解析:根据题意,设函数f(x)=,则f(-x)=),故函数f(x)为奇函数,g(x)为偶函数,则有的几何意义为圆x2+y2=4的上半部分与x=±1、x轴所围成区域的面积,易得

解析:故选D。
解析:令

