函数的零点问题的错解归类剖析

■河南省太康县第一高级中学

函数是高中数学中最重要最核心的内容之一,此部分内容特别丰富,而且知识点众多,但是由于函数的概念比较抽象,学习起来让人十分头疼。下面就函数的零点问题的解决方法和思路与大家分享探究。

要想解决函数的零点问题,首先,熟知函数零点的定义,其次,掌握求函数零点的常用方法:①解方程法;②零点存在性定理;③数形结合法。

例1 若函数y=a x2-2x+1只有一个零点,求实数a的取值范围。

错解：由题意可得,实数a满足的条件为Δ=4-4a=0,所以a=1。

错因分析：忽略了对x2的系数a进行分类讨论,单从表象而误认为已知函数为二次函数。

正解：(1)当a=0时,y=-2x+1,易知该函数只有一个零点;

(2)当a≠0时,由题意可得,Δ=4-4a=0,解得a=1。

综上,实数a的取值范围为{a|a=0或a=1}。

例2 已知函数f(x)=3m x-4,若在[-2,0]上存在x0,使得f(x0)=0,求实数m的取值范围。

错解：因为在[-2,0]上存在x0,使得f(x0)=0,则f(-2)·f(0)＜0,所以(-6m-4)·(-4)＜0,解得。故实数m的取值范围为

错因分析：错解中只考虑到在(-2,0)内部存在x0,使得f(x0)=0,而忽略了所给区间是闭区间,x0也可存在于区间的端点处,即f(-2)·f(0)≤0。

正解：依题意,由f(-2)·f(0)≤0,解得所以实数m的取值范围为

例3 若函数f(x)=x2-2a x+2在(0,4)上至少有一个零点,求实数a的取值范围。

错解：因为函数f(x)=x2-2a x+2在(0,4)上至少有一个零点,所以f(0)·f(4)＜0,即2(1 8-8a)＜0,解得所以实数a的取值范围为

错因分析：错解是因为对至少有一个零点理解不透彻所致,至少有一个零点即有一个零点或两个零点,结合二次函数的对称轴及判别式即可求解。也可分离参数2a=x+,转化为求函数x＜4)的值域。

正解1：因为函数f(x)=x2-2a x+2在(0,4)上至少有一个零点,又f(0)=2＞0,所以f(4)＜0或解得或,即所以实数a的取值范围为

正解2：因为函数f(x)=x2-2a x+2在(0,4)上至少有一个零点,等价于方程至少有一个根,令y=,根据对勾函数的图像与性质,知y≥2 2,当且仅当x=2∈(0,4)时,取等号,所以2a≥2 2,即a≥ 2。故实数a的取值范围为[2,+∞)。

例4 已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点的集合为( )。

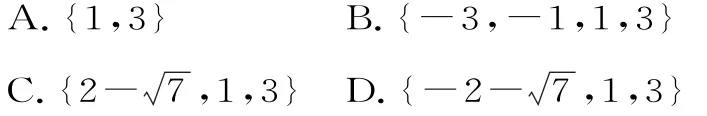
错解：因为函数g(x)=f(x)-x+3的零点为方程f(x)=x-3的解,所以当x≥0时,x2-3x=x-3,解得x1=1,x2=3;又f(x)是定义在R上的奇函数,所以当x＜0时,对应的零点为-1,-3。故选B。

错因分析：错解中把f(x)是定义在R上的奇函数这一性质用到g(x)上了,说明审题不到位。

正解1：设x＜0,则-x＞0,所以f(x)=-f(-x)=-[(-x)2-3(-x)]=-x2-3x。求函数g(x)=f(x)-x+3的零点等价于求方程f(x)=x-3的解。

当x≥0时,x2-3x=x-3,解得x1=1,x2=3;当x＜0时,-x2-3x=x-3,解得故选D。

正解2：数形结合,如图1,由图知点A的横坐标xA＜-3,只有选项D中-2,易知选项D正确。在高考中,数形结合及特殊值代入更显简单快捷。

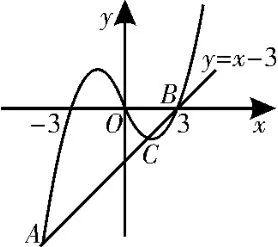
图1

知识点拨：

(1)判断函数在某区间(a,b)上是否有零点。

①判断函数在某区间(a,b)上是否有零点,关键有两点:一是曲线是否是连续不断的;二是f(a)与f(b)是否异号。

②当函数y=f(x)的图像在闭区间[a,b]上不是连续曲线或不满足f(a)·f(b)＜0时,函数在区间(a,b)内可能存在零点,也可能不存在零点。

③当f(a)·f(b)＜0时,f(x)在(a,b)上一定有零点,反之不一定成立。当f(a)·f(b)＞0时,f(x)在(a,b)上不一定没有零点。(请同学们认真思考)

(2)判断函数零点个数的常用方法。

①解方程f(x)=0,则方程f(x)=0的解的个数就是函数f(x)零点的个数。

②数形结合,直接作出函数f(x)的图像,图像与x轴交点的个数就是函数f(x)零点的个数。

③化函数的零点个数问题为方程g(x)=h(x)的解的个数问题,在同一坐标系下作出函数y=g(x)和y=h(x)的图像,利用图像交点判定方程根的个数。

④若证明一个函数的零点唯一,首先证明函数在所给区间上单调,再由零点存在性定理判断函数有零点。

跟踪训练：

1.已知函数f(x)=2a x-a+3,若∃x0∈(-1,1),有f(x0)=0,则实数a的取值范围是( )。

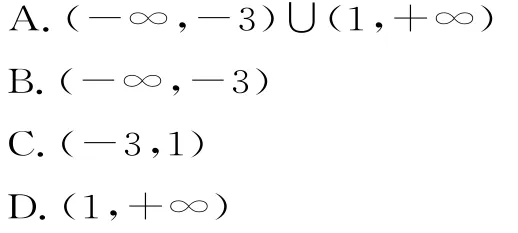
解析：当a=0时,显然不成立;当a≠0时,依题意知f(-1)·f(1)＜0,即(-3a+3)·(a+3)＜0,解得a＜-3或a＞1。故选A。

解析：因为所以若x≠3,由,解得或;若x=3,则a-4=0,即a=4。所以当a=4时满足函数y=f(x)-4有三个零点。故选D。

3.已知函数f(x)=x(lnx-a x)有两个极值点,则实数a的取值范围是( )。

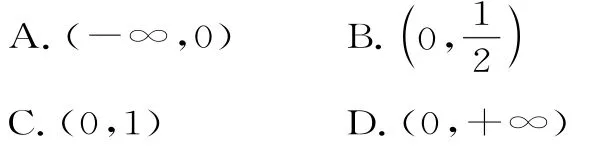
解析：函数f(x)的定义域为(0,+∞),已知函数f(x)=有两个极值点,等价于lnx+1-2a x=0在(0,+∞)上有两个不相等的实数根,等价于函数h(x)=lnx的图像与函数g(x)=2a x-1的图像在(0,+∞)上有两个不同的交点。设函数h(x)=lnx与函数g(x)=2a x-1的图像相切于点A(m,lnm),其中m＞0,函数g(x)的图像在点A处的切线的斜率为k1=2a,函数h(x)的图像在点A处的切线的斜率为,所以。又直线g(x)=2a x-1过点(0,-1),所以k=,所以,解得m=1。所以当函数h(x)与g(x)的图像相切时故所求a的取值范围为故选B。

4.已知函数f(x)=|x2+3x|,x∈R。若方程f(x)-a|x-1|=0恰有四个互异的实数根,求实数a的取值范围。

解析：令g(x)=a|x-1|,则方程f(x)-a|x-1|=0恰有四个互异的实数根等价于f(x)与g(x)的图像有四个不同的交点,故a＞0。分以下三种情况:

②三个交点的横坐标小于1,一个交点的横坐标大于1。则直线y=a(1-x)与曲线y=-x2-3x(-3＜x＜0)相切,且直线y=a(x-1)与曲线y=x2+3x(x＞1)也相切,解得a=1且a=9,显然不可能。

综上所述,所求a的取值范围为(0,1)∪(9,+∞)。

总之,新课标下的高考越来越注重对学生的综合素质的考查,函数的零点问题便是一个考查学生综合素质的很好途径,它主要涉及基本初等函数的图像,渗透着转化、化归、数形结合、函数与方程等思想方法,在培养思维的灵活性、创造性等方面起到了积极的作用。近几年的数学高考中频频出现函数的零点问题,既有小题又有大题,其形式也越来越多样化,但与函数、导数知识密不可分。