数形从分离走向结合,概念理解从浅显走向深刻
陈丽













[摘 要]从数与形两个角度出发,探寻数表征、形表征、数形结合表征概念的教学策略。通过数表征与形表征的相互选择和转化,形成概念认知结构,实现学生对概念的深度理解,进一步增强学生的学习力。
[关键词]数学概念;数形结合;正比例
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)11-0029-03
数学概念因其抽象的内容和静态的呈现方式,使得学生学习数学概念较为困难。如何突破该学习难点?笔者尝试从数学中的两个基本的研究对象数与形出发,探寻通过数形结合揭示概念本质的教学策略。
一、数学概念学习难点分析
数学概念是对现实对象的数量关系和空间形式的本质特征的一种反映。其表现形式是高度概括、精确的语言,学习难点包括两个方面。
1.数学概念内容的高度抽象。在小学数学课本中,概念常常是以描述性的文字呈现的。抽象的文字中往往包含着子概念。例如,人教版教材六年级下册正比例的概念中就包含“相关联的量”“变量”“比值一定”等概念。对六年级学生而言,要感知动态的、连续的、变化的量,以及理解量变化的背后是比值一定,是比较困难的。
2.数学概念的静态呈现。抽象的数学概念如果是图文并茂的,可有助于学生理解。但教材因受篇幅限制,图示往往较少,即使有也是静态的。如教材给出了正比例图像(如图1)。关于“正比例图像是如何形成的?它看着很像折线统计图,有哪些特点?”,学生不得而知。
小学生的思维以直观形象思维为主,对高度概括、抽象的数学概念理解会比较困难。如何突破难点?“数形结合”不失为一种好方法。
二、数形从分离走向结合的数学概念教学策略
数学研究的两个基本对象就是数与形。数与形是表述概念的两种形式,沟通数与形的内在联系,将数与形结合,有助于深入理解概念。
【策略一】从数的角度出发,表征概念。数表征概念是指通过文字、数与代数式三者之间的相互转化,进而便于学习者理解概念。
教学片段1:从数据变化的角度初步认识相关联的量。
思考:下列素材中哪些量在变化?
(1)处于生长发育期的小明的年龄与身高。
(2)一辆汽车行驶的时间和路程。
(3)一本书有100页,已读的页数与未读的页数。
(4)用24个边长为1 cm的小正方形摆长方形。
相关联的量是正比例概念的上位概念,是学习正比例概念的关键。何为相关联?这对学生来说比较抽象。教学中,教师出示四组材料,让学生观察并感受,一个量变化,另一个量也随之变化,从而清楚地认识两种相关联的量,为理解正比例关系做好铺垫。
教学片段2:数、语言描述与代数式之间的转化表征正比例概念。
优优买丝带,买这种丝带的长度与总价的关系如下表所示:
问题:仔细观察,表中有哪两种量?总价是怎样随着长度的变化而变化的?总价与相应长度的比是多少?比值是多少?
借助几个关键的问题,让学生充分经历量的变化过程,从而发现总价和长度之间的变化规律,同时将目光聚焦到变化中的联系,即比值不变,也就是单价始终是一定的,并归纳出数量关系式,实现用数、语言描述与代数式之间的转化来表征正比例概念。
【策略二】从形的角度出发表征概念。形表征概念是指利用实物、图形、图像、符号等表征概念,并通过图形的比较与动态变化达成对概念的理解。
教学片段1:数形对应,动态形成图像。
问题:
(1)数对(1,3.5)的位置在哪里?你能将表格中的其他数对一一表示出来吗?把这些点按一定的顺序连起来(如图3),你发现了什么?
(2)这条线段可以向两端延伸,其中一端延伸到数对(0,0)(如图4)。数对(0,0)表示什么?
(3)找一找数对(10,35)和(12,42)表示的点,把它们描出来,和前面的点连起来(如图5),你又能发现什么?
(4)优优买了a m长的丝带,付了b元,a和b有怎样的关系?
学生在数表征正比例概念时,已初步感知量的连续变化的特征。通过描点、连线,与原点沟通联系,结合教师利用多媒体动态的演示,学生发现a和b都是一对一对出现的。随着直线不断向上延伸,学生清晰地感受到一种量在扩大的同时, 另一种量也在不断扩大。学生经历直观想象、抽象、建立模型等过程,丰富了正比例概念的表象。
教学片段2:在对比点的位置的过程中厘清对应变量中的不变量。
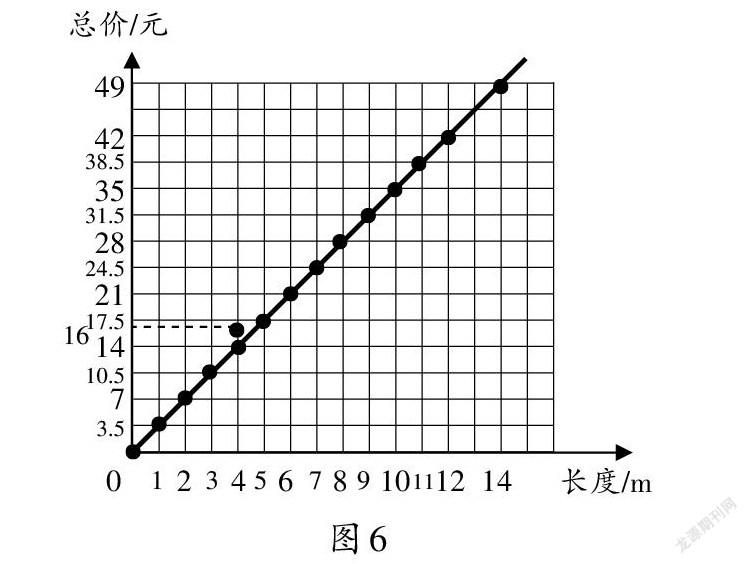
问题:4 m丝带16元,找一找,(4,16)这个点在刚才那条直线上吗?11 m丝带38.5元呢?什么样的点在这条直线上?什么样的点不在这条直线上?
学生在图像动态形成过程中,发现在同一条直线上的这些点,既显示了丝带的长度和单价,又反映了长度和单价之间的关系。两种变量之间的关系是正比例概念教学的难点之一。教学中,笔者增加了根据2组数据描点的环节,其中,一个点在这条直线上,另一个点不在这条直线上(如图6)。通过正例与反例的对比,帮助学生厘清两个变量之间的关系——背后的不变量,形成正比例图像,初步感受函数思想。
【策略三】数表征与形表征互相转化,形成综合图式表征概念。
教学片段1:在形表征中找数。
问题:如果买9 m的丝带,你能根据图像判断总价是多少吗?49元又能买多长的丝带?(答案见图7)
正比例图像的形成并不意味着教学的结束。教学中,让学生依据图像,由一个量的值推断、估计另一个量的值,由一种量之间的关系推断另一种量之间的关系。学生可以根据图像的特点进行推理,将形转化为数,体会函数的形表征和数表征之间的联系。
教学片段2:在数表征中思形。
小乌龟和小螃蟹比赛,爬行时间和爬行距离如下表所示:
问题:想一想,小乌龟和小螃蟹的爬行时间和爬行距离成正比例关系吗?
观察小乌龟和小螃蟹的爬行情况图像(如图8),想一想,图像中的两条直线分别代表哪一种小动物的爬行情况?后来小海龟也参加了比赛,他的爬行速度比小螃蟹还要快一些,你觉得他的爬行情况图像可能是怎样的?
这里借助两种动物爬行时间与距离的数据,在同一幅图中,用图像表征速度快慢的樣子,以数思形;通过数形、形形对比,感悟数与形的对应关系,以数解形,深刻体会正比例概念的本质。
【策略四】在概念沟通中,形成概念综合图示。
概念综合图示的形成,需要将概念的形成过程与结果进行沟通,将概念的各种表征形式进行沟通,将已学的概念与后续延展的内容进行沟通。
(1)在回顾中沟通。从具体的实例出发,回顾经历数据的分析、比较与抽象,图像的动态形成以及特征等研究过程,沟通正比例概念的文字表征、代数式表征和图像表征之间的联系,形成正比例图像。
(2)在延伸中沟通。从纵向出发,与后续研究内容进行沟通。初中学习的正比例图像,是一条过坐标原点的直线。通过延伸,沟通了正比例概念文字与图像的联系。
(3)在比较中沟通。从横向出发,将相关联的概念进行沟通。在学习正比例概念之后,教师顺势引导:“正比例和反比例之间有什么区别与联系?你能从四组材料中找出成反比例关系的那一组吗?”为学生形成函数概念图示做好准备。
在概念的教学中,挖掘概念中的“数”是什么、“形”是什么,采用以形助数或以数解形的方法,从数表征、形表征、数形结合表征概念入手理解概念。在数表征概念中,力求提供丰富的实例,在分类与比较中形成概念表象。在形表征概念中,借助现代教育技术等展示形的动态变化,力求通过观察、操作、想象形成概念之形表象。在数形结合表征概念时,力求让数表征与形表征互相转化。由数思形,由形译数,使学生经历数与形的对应、数与形的转化过程,形成综合概念图示,以达到对概念深度理解的程度。
(责编 吴美玲)

