有序表征:认知从“呈现”走向“发现”
丁洪 顾刘兵
[摘 要]列举策略的表征一般经历两个阶段,即“呈现过程”和“发现联系”。其中,“呈现过程”侧重信息的初步加工,使关键事件“看得见”、过程经历“走得稳”和经验对接“理得顺”,在解决显性问题中提炼策略;“发现联系”侧重信息的精细加工,能灵活迁移“用得上”、模型建构“想得透”和思想沉淀“带得走”,在探究隐性规律中内化策略。策略学习需要两个阶段互为补充、循环往复和辩证统一。
[关键词]列举策略;呈现过程;发现联系
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)11-0010-03
“用列举的策略解决实际问题”是苏教版教材五年级上册编排的“策略学习”的专题活动,它是运用策略解决实际问题的种子课。从表征需求看,问题过程复杂,阶段结果多样,一一呈现可以消除误解,策略意识的激发由内而外;从表征要点看,旨在引领学生经历策略的生长过程,感悟“不重复和不遗漏”的操作关键,策略思考的提炼由粗变精;从表征价值看,可以解决显性问题,还可以探究隐性规律,策略认知的发展由近及远。问题是,“如何做到呈现过程有条不紊,有针对性地解决问题?”“如何做到发现规律丝丝入扣,有系统性地探究联系?”“如何处理好呈现和发现的关系,使得策略认知螺旋上升和有序建构?”,弄清楚这些核心问题才有助于有效开展列举策略的教学。
一、有序呈现过程,解决显性问题
策略是指导数学活动的计划、方案和技巧,是对具体数学认知的调控、修正和优化。对小学生而言,策略学习离不开具体问题情境、过程充分经历和经验合理对接。
1.关键事件“看得见”
策略学习需要情境,在具体情境中,某些环节、片段或案例发挥的价值较大,这样的对象可称为策略学习的关键事件。
以A教学为例,它是围绕南通洲际绿博园设计情境。首先,用视频形式带领学生欣赏典型景点,如“梯田花海”“热带名花雨林馆”和“木化石风情园”等;公布“今日行程”,即“种植基地”“时光隧道”“美食区”和“娱乐区”,将学习内容分别嵌于活动板块,整体勾勒出关键事件的节点和流程。B教学是改造苏教版教材中的例题,将“怎样围面积最大?”的线性思考变成“要围一个面积为20平方米的长方形花圃,如果22根1米长的木条全部用完,且不能折断,这个任务能完成吗?”的多元思辨,展示过程中紧扣“周长一定时,面积能否符合要求?”和“面积一定时,周长是否滿足需求?”这两个关键事件,同样架构了整个教学时空。
显然,以上两个教学设计的关键事件的角色定位和演绎方式明显不同:A教学侧重生活情境的系统性,关键事件先预设再展开;B教学侧重数学问题的思辨性,关键事件先生动再深刻,但这两个教学的可视化诉求又有一致性。
2.过程经历“走得稳”
认知是人最基本的心理过程,它特别强调通过必要的信息加工获取知识。因此,为了增强心理体验的强度,同时提高信息加工的效度,过程经历需要考量“是否充分、是否完备和是否稳妥”,这是策略认知发展的要求。
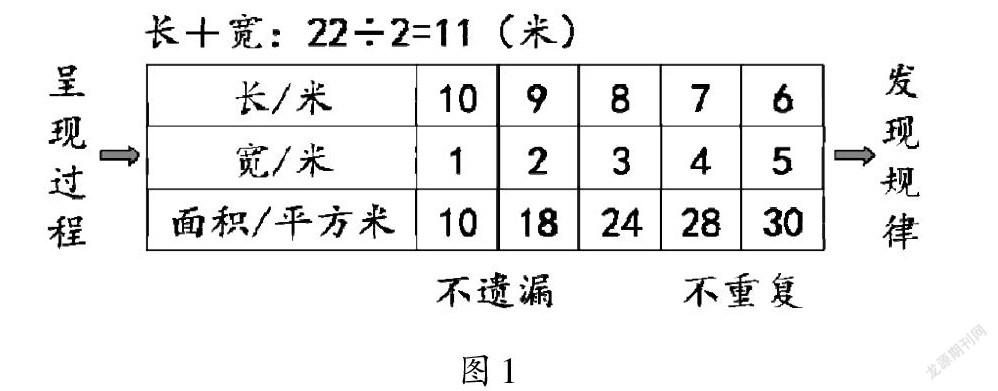
以A教学为例,先在“种植基地”中出示“王大叔用22根1米长的木条围一个长方形花圃,怎样围面积最大?”的问题,驱动学生分析已知条件和问题,得到“周长是22米,可以围成大小不同的长方形”和“围成的长方形的长和宽都是整米数”的结论,这里主要将生活信息加工成数学信息。接着,通过问题“你打算怎样解决上面的问题?”引导学生提出“用22根小棒摆出不同的长方形,再分别求出它们的面积”和“先求出长方形长与宽的和,再通过列举求出面积各是多少”的方案,这里主要是将数学信息转换成数学思维。然后,创设自主探究活动,引导学生先在活动单上记录过程,再在小组内交流、互动和点评,直至全班展示汇报。由汇报结果知,从方法层面上看,有画出过程和计算过程之别;从思维层面上看,有推进有序和推进杂乱无章之分;从结果层面上看,有解决问题和阻碍结论之态。对于学生充满生机和活力的原创作品,教师应当尽可能地展示和对比,还要回溯到问题原点,考量“长方形面积大小”的决定因素,顺势锁定长和宽的乘法组合,有机渗透二维平面观念,这里主要将数学思维加工成数学结构。最后,鼓励学生紧扣问题的本源性结构,在表格中快速、有序地列举所有可能,对应计算各自面积后,获得“长6米、宽5米时,长方形面积最大”的终极结论,这里主要将数学结构加工成数学路径。
以B教学为例,教师将教材中的例题改编成研学单,让学生课前先尝试探究问题“王大伯想用22根1米长的木条围一个面积为20平方米的长方形花圃。如果22根木条要全部用完,而且不能折断,你觉得他能完成这一任务吗?”。这种前测设计,从学的角度看,能为学生的自我挑战提供平台,而且时间充裕,学生可以更好地思考和表征,尽己所能,不留遗憾;从教的角度看,教师可以了解和捕捉学生的思维过程,感受他们的认知倾向、表达习惯和思维质量,有效弥补了解不全、交流仓促和即时评价有局限的不足,真正做到知己知彼,有的放矢。回到课堂上,教师首先组织学生在小组内交流各自的方法和结论,并展示典型作品:第一种是“尾巴型”,先设计长5米、宽4米的长方形,再将剩下的4米长的木条接在图形尾部;第二种是“靠墙型”,设计长20米、宽1米的长方形,这个长方形的一条长边是靠墙的;第三种是“支架型”,先设计长5米、宽4米的长方形,再将剩下的4根木条分别放在图形四个角的下方,这样就将原来设计的长方形支撑起来了。学生的评价头头是道:有学生认为“尾巴型”没有考虑“22根木条要全部用完”这个条件,可谓“一针见血”;有学生认为“靠墙型”虽然用完了所有木条,但是否靠墙值得商榷,而且既然可以一面靠墙,那么是否可以两面、三面靠墙呢?可谓“面面俱到”;有学生认为“支架型”虽然有意思,但是在长方形面积不变的情况下,除了四个角可以放置木条,其他很多地方都可以,结论不唯一和不明确,可谓“丝丝入扣”。另外,有学生认为不能完成任务:一是通过周长是22米,分别列举不同长方形的长和宽,计算后得出面积都不等于20平方米;二是通过面积是20平方米,分别列举不同长方形的长和宽,计算后得出周长都不等于22米。
显然,通过以上两个案例可以发现策略学习的共性,那就是策略推进过程要想走得稳,既要有机结合问题的精神和实质,也要适时凸显策略的特质和魅力,两者不可偏废,否则策略学习犹如空中楼阁,看似有结论,实则无过程。
3.经验对接“理得顺”
经验可以分为两个层面。一是感性层面的即时经验,它可以是本节课内的,也可以是本单元内的,经验产生的时间比较近,经验载体相对集中;二是潜意识层面的过往经验,它可能是跨学期的,或者是跨学段的,经验产生的时间比较长,经验载体相对分散。
在A教学中,首先让学生通过思考“回顾解决问题的过程,你有什么体会?”,梳理出“有些实际问题可以通过列举来解决”“按一定的顺序列举,做到不重复、不遗漏”和“要对列举出的结果进行比较,做出选择”的即时经验,助推经验的沉淀。接着,在“时光隧道”环节,通过 “在以前的学习中,我们曾经运用列举的策略解决过哪些问题?”驱动学生自主回忆和小组内碰撞,梳理出“一组一组地写出10可以分成几和几”“用12个边长为1厘米的正方形拼成不同的长方形”和“有序地写出3张数字卡片能组成的所有三位数”等策略,虽然整数的分成、图形的拼成和多位数的组成等只是过往经验的冰山一角,但是它们的存在足以说明列举策略的客观性、适用性和价值性。与此对应,在B教学中,问题情境和问题内容虽然不尽相同,但是经验对接这件事一直在发生和发展。有趣的是,它们其实都在努力做到即时经验与过往经验的碰撞、对接和交融,使得策略经验从简单固化走向了路径塑化(如图1)。
显然,A教学提供的显性问题相对封闭,B教学创造的显性问题相对开放,但是它们都需要通过各自显性问题的顺利解决,借助关键事件的聚焦、过程经历的体验和经验的无缝对接,使得丰盈的体验能助力策略的感知和感悟。
二、有序发现联系,探究隐性规律
以上学习只是对特定信息进行了必要的对比、抽象和提炼,学生的策略认知处于低水平运行状态。其实,可以适度迁移运用和适时深度加工,以挖掘信息之间的联系,探明隐藏于现象背后的数学规律,这样的策略体验才完整、系统和有价值。
1.灵活迁移“用得上”
首先,出示“哪个时点会响铃?”的问题,引导学生分析已有闹铃信息,归纳出“每间隔40分钟响一次铃”的规律,然后进行列举和判断。这里的具体情境虽然有变,但是列举需求仍然不变。接着,出示“一共有多少种不同的搭配?”的问题,引导学生先从一种荤菜开始列举,得到荤素4种不同搭配,然后以此类推,得到“3個4种,一共就是12种”的结论;还可以从一种素菜开始列举,得到素荤3种不同搭配,然后以此类推,得到“4个3种,一共就是12种”的结论。这里的思维起点虽然不同,但是列举策略异曲同工。最后,出示“可能得到多少环?”的问题,引导学生剖析“投中两次”的内涵,即“环数相同”和“环数不同”两类,据此分别进行列举。需要注意的是,“8+8=16”和“10+6=16”的投中过程不同,但从问题“多少环”这个角度考量,它们又归属于同一种环数,这里的列举意图虽然明显,但是列举结果仍需整合。显然,单线型列举是组合型列举和分类型列举的基础,了解它们之间的有机联系,可以更好地解构复杂问题和把握策略方向。
2.模型建构“想得透”
模型建构是用联系的视角对数学信息进行再加工,这个过程数学味浓郁,“一案一得”是常用的方法和路径。比如,在“谁的面积最大?”的问题中,引导学生“从左往右”观察长和宽的单独变化,“从上往下”观察长和宽的组合变化,归纳出“周长一定时,长和宽越接近,面积就越大”的规律;在“哪个时点会响铃?”的问题中,引导学生“从前往后”观察响铃的时点,发现“相差以两小时为一个周期”的周期规律;在“一共有多少种不同的搭配?”的问题中,引导学生按照“先后顺序”观察搭配对象的数量,发现“3个4种”和“4个3种”的内在联系,归纳出“搭配数量×搭配数量=搭配结果”的乘法规律;在“可能得到多少环?”的问题中,引导学生从“先分再合”的角度观察列举过程,发现看似复杂的问题其实可以合理分解,感悟分类讨论解决问题的叠加规律。显然,模型建构难度不一,不能要求学生一下子就领悟,尤其对解决相似的问题有困难时,仍然可以回到问题起点,一一列举解决问题后再次建模。
3.思想沉淀“带得走”
数学思想是系统化、理论化、理性化了的数学知识,是对数学科学研究的本质及规律的深刻认识。这样看来,数学思想是数学学习的“根”和“魂”,是学生能从数学学科中带得走的宝贵财富,策略学习同样需要数学思想适时介入、适度发展和适切点化。比如,在“谁的面积最大?”的问题中,要使长方形面积的大小可视化,就可以渗透“数形结合”的基本思想。这样除了有数据支撑的理性推理,还有感性体验的直观把握,使得策略学习入眼入心、印象深刻;在“一共有多少种不同的搭配?”的问题中,为了使搭配过程和结果得以简洁化,可以渗透“整体思考”的基本思想,无论列举起点怎么变化,只要搭配的数量不变,它们的搭配结果就对应不变,策略学习从有限列举走向了无限思考;在“可能得到多少环?”的问题中,为了使复杂问题的内涵表征序列化,可以渗透“分类讨论”的基本思想,这样既有分门别类的单点突破,又有井然有序的多点整合,策略学习从有序解构走向了合理重构,等等。显然,有了数学思想的充分浸润,策略学习的过程将更有生命力,策略内化为数学素养也就更加自然、顺畅和高效。
综上所述,“呈现过程”是列举策略学习的基础工作和必由路径,主要通过不同过程的展示、评价和概括,逐步抽象共性的认知,感知策略存在的环境、把脉策略运行的要点和辨析策略表征的对象;“发现联系”是列举策略学习的有序延伸和必要拓展,主要通过不同情境的策略迁移、不同模型的顺利建构和不同思想的有序渗透,助力学生认知水平的逐步提升。需要说明的是,两者虽然可以和谐共生、循环往复,但是切莫急功近利、本末倒置。
[本文系江苏省教育科学“十三五”规划重点课题《基于问题链驱动的小学生数学化学习的研究》(课题批准文号:C-b/2020/02/26)和江苏省中小学教学研究第十三期重点课题《深度学习下小学数学游戏的开发与应用研究》(课题批准文号:2019JK13-ZB48)的阶段性成果。]
(责编 金 铃)

