通过实践渗透,提高数学思维能力

刘霖哲

【摘要】数学学习其实就是对数学思想方法进行了解、掌握、运用的过程，能够通过利用学到的数学思想，将实际生活中遇到的问题有效解决，对具体事物的运动变化过程进行全面描述，从而采取具有较高针对性和可行性的解决方案.本文以高三学生的视角出发，针对高中函数教学数学思想进行详细分析，通过不断实践渗透，提高高三学生的数学思维能力.

【关键词】高中数学;函数教学;数学思想

函数不仅是我们对客观世界运动、变化、发展规律进抽象化理解以及全面描述的一种模型，而且是组成高中数学的核心知识内容之一.作为组成我国高中数学结构的重要因素之一，函数也是高中数学学习的重要知识内容，在高中数学学习中，函数具有较强的基础概念特征，是学生灵活运用不等式、方程式、几何知识解决具体问题的基本工具.在高考中，许多知识点都是对我们是否具备抽象思维能力进行考察，因此，在高中数学函数学习中合理使用数学思想，是学生掌握多元化数学知识过程中必须经历的重要环节.高中生不仅要对数学思想在提高自身函数学习效率过程中具有的重要性给予正确认识和高度重视，而且还要将数学思想作为函数学习的基本策略和指导核心，这样才能有效实现提高我们函数学习质量以及数学素养的目标.

1 数学思想的定义

对于数学思想而言，就是在具体学习内容以及学生认识、了解数学的过程中，提出一些科学的数学观点，最终目标是确保学生能够真正感受数学的内涵、了解数学的本质.在开展高中数学学习的过程中，我们分析和解决数学问题的具体思路，就是一种数学思想，能够使学生找到正确解题思路和方法提供帮助，有效提升学生的数学素质和能力的同时.

2 高中数学函数数学思想的有效渗透途径

2.1 在函数数学概念中理解数学思想

作为一名高三学生，在高中数学学习的过程中，想要确保能够将教师传授的新数学知识全面掌握，我常从以下几个层面入手：

第一，对相关知识的概念充分了解.要结合自身实际学习能力，对具体概念的形成过程进行详细解读，确保自身在接触全新数学知识的同时，对数学思想在形成数学概念过程中具有的重要性给予正确认知.我首先要对教师结合具体教学内容设计的函数概念形成过程充分理解，确保能够对函数的形成原理明确掌握，然后再将概念融入到教材内容中进行全面梳理.

例如 在解决以下三个函数的奇偶性问题时，f（x）=x3、f（x）=x2、f（x）=5x+3，其中x∈（-∞，+∞），我结合教材内容对x的定义域进行准确判定.接着对x的定义域进行仔细观察，并思考教师提出问题：当x在定义域中的具体取值为两个互为相反数的数值时，对应函数值之间的关系是否存在变化？通过具体解析对得到结果进行判断和理论验证，使我明确了解答案内容.通过这样的方式，就能是我全面概括出奇函數和偶函数的定义.

第二，通过对函数定义的深入剖析，使我深刻体会函数概念的内涵.在教师的引导下，我对相关定义具有的相同之处和不同之处进行对比，从“定义中的任何一个x都有某个相同点”这一角度出发，分析“任何”和“都有”等具体关键词的含义，并利用函数f（x）=5x+3对这个定义进行验证.接着，通过掌握x和定义域之间的关系，充分了解奇函数和偶函数定义域关于原点对称是判断函数奇偶性的第一步，再利用x与-x的函数值的相等或相反的关系，掌握如何判断函数奇偶性的方法.为了加深自身对函数概念内涵和本质的充分理解，应该深入体会具体内容提出问题，并对问题的答案进行验证.

例如 判断当x∈（-1，1]和x∈[-1，1]时，对y=2x2、y=3x3是奇函数还是偶函数.我在解题过程中，应该利用思维导图的方式，将判断函数奇偶性的相关必要条件逐一罗列出来，通过整理和总结，得到“函数的定义域关于原点对称”这一答案.通过这样的方式，不仅能够使我加深对函数定义的本质、内涵加深记忆，而且还能使具有较高抽象化的函数定义逐渐转变为寻常的已知方法，从而使数学思想内涵具有的作用和价值充分发挥到数学函数学习中，有效提高自身对函数相关知识点的学习效果.

2.2 在例题学习中，加强对数学思想的有效渗透

第一，在提高自身对函数知识的转化能力的过程中，我利用了方程思想.这是因为在高中数学教学中，函数知识和方程知识是两个重要的组成结构，二者具有相辅相成的特点.通过对函数知识和方程知识的合理应用，能够将具有较高复杂性和抽象性的函数问题有效简化，使我的解题思路更加清晰.

例如 在解决“函数图像f（x）=ax3+bx2+cx+d经过点（0，0）、（1，0）、（2，0），且f（-1）<0如何判断b的取值范围”此类的问题的过程中，通过对已知条件的分析，每个坐标点都能满足函数关系式，因此，可以将方程思想结合其中，解决函数问题.我列出方程d=0

a+b+c=0

8a+4b+2c=0

，从中能够得出a=-b3

c=-2b3的结论，因此，判断f（x）=-b3x3+bx2-2b3x=-b3x（x-1）（x-2）

，并且将f（-1）<0带入其中，最终得出b<0的答案.

第二，在提高自身解决数形结合问题能力的过程中，加强对函数图像的有效利用，通过画出函数图像，能够是我对函数问题的性质进行直观分析，从而利用函数图像解决具体问题，这也是我利用数形结合思想解决具体问题的表现方式之一.

例如 我在解答数学方程：x2+（a-1）x+1=0的过程中，已知该等式有两个相异实根，并且这两个实根都在区间[0，2]中，那么，a的取值范围为多少？在解题过程中，我先画出函数的图像，从图像中得出△=（a-1）2-4>0;0<-a-12<2;f（0）≥0;f（2）≥0，重新整合、分析，能够判断a∈[-32，-1].在解决此类问题的过程中，关键点在于我是否拥有函数思想，通过对二次函数图像性质的充分利用，从中找到隐藏的不等式关系，确保相关问题得到快速有效的解决.

第三，我通过对函数性质的灵活运用，能够提高自身分类讨论能力.在学习高中数学函数知识的过程中，无论是对数函数还是指数函数，都离不开分类讨论.因此，我可以将例题充分融入到具体解题中，使数学解题思想通过例题得到充分呈现，必然能够大幅度提高我的分类讨论能力.

例如 我在解答不等式loga（x+1-a）>1的过程中，由于底数a为参数，因此，要针对底数a进行分类讨论.当01时，能够得到{x|x>2a-1}的结论.

第四，在解决函数问题的过程中我发现，会涉及到大量数学思想，我只有经历具体解决过程，才能充分理解并掌握相关数学思想，提高自身灵活、准确应用数学思想的能力.因此，我必须加强对函数教学中数学思想的深入挖掘，将其具有的作用和价值充分发挥出来.

例如 在解决不等式log2（x2-3x-4）>log2（2x+10）的过程中，我应该先消除不等式中的对数符号，从而得到不等式组x2-3x-4>0;2x+10>0;x2-3x-4>2x+10，这样我就可以通过解决不等式组得到最终答案，{x|-5<x<-2或x>7}，使化归的数学思想具有的作用得到充分发挥，提高我的函数解题能力.

2.3 在解题训练中，加强对数学思想的应用

我在解决函数问题的过程中，经常会接触到大量数学思想，我只有经历具体解决过程，才能充分理解并掌握相关数学思想，提高自身灵活、准确应用数学思想的能力.因此，我应该加强对函数教学中数学思想的深入挖掘，将其具有的作用和价值充分发挥出来.

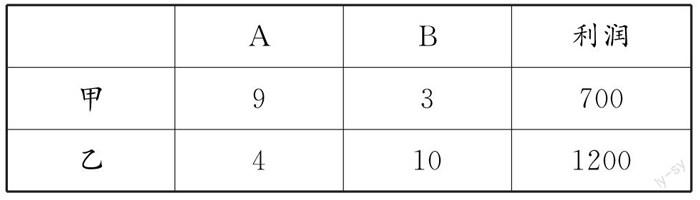
例如 我在解决下面这道函数问题时，会使用列表法.某超市采购了两种酸奶，A种酸奶每袋360G，B种酸奶每袋290G，超市原计划利用这两种酸奶和其他水果制作甲、乙共50盒水果捞，已知，制作甲种水果捞需要A种酸奶9G、B种3G，能够获得利润共700元，制作乙种水果捞需要A种酸奶4G、B种10G，能够获得利润共1200元.（1）若共同生产甲、乙两种水果捞有几种方案？（2）若共同生产甲、乙两种水果捞的总利润为y，其中一种水果捞的生产数量为x，请列出x与y之間的函数关系，并且以函数性质的角度，对问题（1）中那种生产方案能够获得的利润最大进行说明，并计算出最大利润是多少.

在分析这道函数问题的过程中，我发现一共出现过9个数据，这些数据与AB两种酸奶的重量、甲乙两种水果捞的数量以及获得的利润有关，为了对题目中出现的这些数据进行全面梳理，我会将这些数据整理成表格.

解

（1）假设生产甲种水果捞的数量为x，则乙种水果捞的数量为50-x，从而结合题目能够得出不等式组9x+4（50-x）≤360;3x+10（50-x）≤290，通过计算不等式，最终能够得到30≤x≤32.由于x为整数，因此，甲种水果捞的数量的选择范围为30、31、32，对应乙种水果捞的数量为20、19、18.从中能够得到实际生产方案有3种：（A）甲种水果捞的数量为30、乙种水果捞的数量为20;（B）甲种水果捞的数量为31、乙种水果捞的数量为19;（C）甲种水果捞的数量为32、乙种水果捞的数量为18.

（2）根据已知条件我能够列出等式y=700x+1200（50-x）=500x+60000，这个等式中，x只能为30、31、32，由于0>-500，因此，y的数值随着x的增加而减小，二者成递减关系.当x=30时，y的数值最大.接着，我结合（1）中的第一种生产方案落实具体措施，能够确保得到的利润最大：-500×30+60000=45000（元）.

3 结语

高三学生应该对数学学习理念和学习措施给予了高度重视.通过对现代数学思想的不断理解、掌握，不断提高自身创造性思维和个性化发展水平，确保自身在学习具体知识的过程中，具备主动探索的思维意识，使自身能够深入观察、系统分析实际生活中存在的问题，具备利用所学知识解决实际问题的能力，提高自身主动学习数学知识的兴趣.长此以往，不仅能够使高三学生数学学习能力、学习质量、学习效率得到进一步提升，而且还能强化我们的数学学科素养，使学生的综合竞争能力得到全面提升，为成为促进社会发展必不可少的复合型人才奠定坚实基础.

参考文献：

[1]白治成.高中数学函数教学数学思想的实践渗透分析[J].新课程（教师版），2019，000（005）：61.

[2]白治成.高中数学函数教学数学思想的实践渗透分析[J].新课程·下旬，2019（5）.

[3]梅龙伟.高中数学函数教学数学思想的实践渗透分析[J].信息周刊，2019，000（052）：P.1-1.