基于问题解决的数学单元教学设计

邢雪文

［摘  要］ 研究者以问题解决过程线索为主题的单元教学模式，对“二元一次方程组”进行单元教学设计.设计思路为“总分总”路径，从教学内容组织、教学目标设计、素材组织、作业布置、评价与反馈五方面进行单元教学设计.

［关键词］ 单元教学；问题；方程；教学设计

问题提出

单元教学法是落实学科核心素养的重要抓手，单元教学法借助大背景、大问题、大思路、大框架进行高观点统领、思想性驾驭、结构化关联，能有效规避传统的课时教学整体感不强、知识分解过度、学习碎片化、教学效益低下的现象［1］. 学生学科核心素养的培养要求教师的教学设计从设计一个知识点或课时转变为设计一个大单元［2］，把每节课的知识置于整体知识的体系中，注重知识的结构和体系，让学生感受数学的整体性.

以问题为导向的单元教学设计，可以帮助学生理解学习某一知识的必要性和可行性，使学生参与发现新知的全过程，包括发现问题、提出问题、分析问题、解决问题等过程. 学生在参与学习的全过程中既能学会有关知识技能，又能掌握学习的路径与方法.

“二元一次方程組”是初中数学在一元一次方程之后的内容，两者之间存在密切联系. 学生在学习二元一次方程组时，往往会产生疑问：为何要学二元一次方程组？明明可以用一元一次方程解决，为何一定要用二元一次方程组？二元一次方程和一元一次方程有什么联系？部分教师在教学时，将教学内容和教学目标碎片化，最后一些学生只学会解二元一次方程组，没有意识到解二元一次方程组只是应用二元一次方程组解决实际问题过程中的一部分. 还有一些学生缺乏整体性知识体系，不能和已知的一元一次方程建立联系，不能发现研究方程问题的一般思路.

设计思路

单元教学的核心思想是系统思维，教师应从整体上系统性地确定教学目标，组织教学内容［3］，培养学生从整体上了解知识的来龙去脉，把握知识的本质，理解知识间的联系，掌握数学的思想方法，灵活选择和运用知识解决实际问题，提高系统化解决问题的能力.

喻平教授提出了单元教学法的四种主题教学模式：以问题解决的过程线索为主题、以建立个体CPFS结构为主题、以概念的发展为主题、以数学思想方法解决问题为主题［2］. 笔者采取以问题解决过程线索为主题的单元教学模式，以“二元一次方程组”的教学为例，以问题导入，让学生在解决和分析问题的过程中，发现若干新问题，再对新的问题不断追根溯源，直到与已有知识建立起联系来解决问题［2］. 一方面以问题驱动学生深度思考，思维深度参与课堂，切实提升思维水平；另一方面让学生在整体上理解知识间的关联，系统化地解决实际问题，完善自身知识体系，提高问题解决能力和数学核心素养.

教学过程设计

（一）教学内容组织

单元教学的基本路径是“总—分—总”，首先通过适当的方式让学生对学习单元有一个整体的感知，然后根据单元的结构进行分解学习，最后在分解学习的基础上再次进行综合提升，形成更为全面的整体理解.

本单元采取“总分总”的模式. 第一个“总”将用二元一次方程组解决问题情境作为第一课时的主要教学内容，目的是让学生从整体上把握本单元内容的框架；“分”学习二元一次方程组的概念、代入法和加减消元法解二元一次方程组、解三元一次方程组；第二个“总”完善第一个“总”的问题，并对本单元知识进行深刻总结完善，拓展应用，扩展学生认知结构.本单元的教学始终围绕明、暗两条主线（如图1）. 明线是用二元一次方程组解决实际问题的过程中所用到的数学知识与技能，暗线是体会模型和化归的数学思想，掌握研究方程问题的思路.

（二）教学目标设计

《义务教育数学课程标准（2011年版）》对本单元教学目标要求如下［4］：

①能根据具体问题中的数量关系列出方程，体会方程是刻画现实世界数量关系的有效模型；

②掌握代入消元法和加减消元法，能解二元一次方程组；

③能解简单的三元一次方程组（不做考试要求）.

现对本单元教学目标进行调整如下：

①能够用二元一次方程组解决实际问题，体会与一元一次相比解决问题的便利性与可行性；

②理解二元一次方程组的概念，并能把握其与一元一次方程区别与联系；

③能够灵活选择代入法和加减消元法解二元一次方程组；

④能解三元一次方程组，并思考解多元一次方程组的方法；

⑤掌握二元一次方程组的学习思路，并和一元一次方程进行对比，发现两者的异同；

⑥体会方程是刻画现实世界数量关系的有效模型，提高数学建模能力；

⑦能将解二元一次方程组转化为解一元一次方程，将三元一次方程组转化为二元一次方程组的过程中，体会化归思想方法.

（三）素材组织

“二元一次方程组”内容包括三个方面：从问题到方程、解方程组、用方程组解决问题. 具体教学设计和课时安排如表1.

由于篇幅有限，这里只以问题串形式，简要展示各个课时学习的思路.

第1课时

问题1. 篮球比赛规则规定：赢一场得2分，输一场得1分.在中学生篮球比赛中，某球队赛了12场，共得20分.该球队赢了几场？输了几场？

生：设赢了x场，输了（12-x）场，则2x+（12-x）=20，求出x就可以.

追问1.1：如果设赢了x场，输了y场呢？你能找到几个相等关系，列出几个方程？

生：两个，x+y=12；2x+y=20.

追问1.2：设一个未知数就可以解决，为什么还要设两个未知数呢？

问题2. 《希腊文选》中有这样一题：驴子和骡子驮着货物并排走在路上，驴子不停地埋怨驮的货物太重，压得受不了. 骡子对驴子说：“你发什么牢骚啊！我驮的比你驮的更重.倘若你的货给我1口袋，我驮的货比你驮的货重1倍；而我若给你1口袋，咱俩才刚好一样多.”驴和骡各驮几口袋货物？

这个问题你认为设几个未知数更好找到等量关系，解决问题？你准备怎么设？

生：设骡子驮x袋，驴子驮y袋.可以得到两个方程：x+1=2（y-1）；x-1=y+1.

追问2.1：设一个未知数可不可以呢？你觉得哪个更方便？并说说理由.

生：可以. 但设两个未知数更方便，因为两个相等关系更好找.

追问2.2：如何求得两个问题中的未知数x，y？

设计意图 以两个实际应用二元一次方程组的问题引入，问题1用一元一次方程解决很方便.问题2以《希腊文选》中的故事为背景，一方面以“复制式”直接引用数学史，渗透数学文化；另一方面这个问题用二元一次方程组更加简便，让学生体会学习二元一次方程组的必要性. 虽然此时学生还没有二元一次方程组的概念，但是有列方程的经验，因此学生可以找出相等关系，建立方程模型.通过类比一元一次方程，要解决这个问题，就是要找到两个未知数的值，由此得到相关概念：二元一次方程、二元一次方程组、二元一次方程的解、二元一次方程组的解的概念，以及解这个二元一次方程组的两种方法——代入消元法和加减消元法，从而形成整体的研究思路（如图2）：

第2课时

问题3. x，y的值如何求？

追问3.1：要想得到x，y的值，我们首先要清楚x，y是什么意思，类比一元一次方程中未知数的值，你能说清楚吗？

生：满足方程的取值.

追问3.2：满足哪个方程？

生：两个都满足.

追问3.3：这两个方程和一元一次方程比有什么区别与联系？

生：都是整式方程，所含未知数的项的次数都是1. 一元一次方程只有一个未知数，但是新的方程有两个未知数.

追问3.4：你能否模仿一元一次方程，给这样的方程下一个定义？

设计意图 学生对本单元内容有了整体的概念，为了解决第一课时留下的问题，将问题一步步分解：要求x，y，首先要明确二元一次方程组解的概念，其次要知道二元一次方程组和二元一次方程的解两个概念，最后要知道二元一次方程的概念. 通过如何求x，y这一个问题，引导学生通过类比一元一次方程有关概念，一步步思考，自然而然地得出相关概念，了解概念为何而来，有何作用，理解概念本质.

第3课时

问题4. x，y的值如何求？

追问4.1：我们目前只学过解一元一次方程，能否将二元一次方程组转化为一元一次方程来解？

生：应该可以.

追问4.2：一元一次方程和二元一次方程的区别在于未知数的个数不同，那么我们如何将二元一次方程组的未知数去掉一个，你能否从问题1中的两种方法中得到启示？

生：只要将2x+y=20中的y用（12-x） 代替就可以求出x的值.

追问4.3：如何求y呢？

生：再代入上面的两个方程，或者y=12-x就可以.

追问4.4：能否先消x，先求出y，再求x呢？

设计意图 与问题3相同，这里引导学生解二元一次方程组的具体方法，追问4.1引导学生将二元一次方程组转化为一元一次方程问题，解出一个未知数，再求出另一个未知数即可.这是本单元转化思想与消元法暗线的体现，由此引出代入消元法，让学生明白代入消元法从何而来，而不是直接给出解方程的固定模板. 通过追问4.4，学生会进一步理解代入消元法的本质是通过一个未知量表示另一个未知量，代入方程，将二元一次方程转化为一元一次方程来解.

第4课时

问题5. 观察方程组x-y=3，

x+y=5，除了可以用代入消元法，还可以怎样进行消元来解决问题？

生1：把两个方程相加，就可以消去y，得到2x=8，x=4.

生2：把两个方程相减，就可以消去x，得到y=1.

追问5.1：这个方程组能够进行加减消元的前提是什么？

生：相同的未知数前面的系数是相同的或者互为相反数.

问题6. 能否用同样的方法解二元一次方程组？

5x-2y=4，  ①

2x-3y=-5.  ②

生：（犹豫）有的说可以，有的说不知道.

追问6.1：如何将这个方程组同一个未知数前面的系数化为相同或互为相反数？

生：找最小公倍数！

追问6.2：如何找？

生1：①×2，②×5.

追问6.3：还有没有其他的方法？

生2：①×3，②×2.

追问6.4：此时一个新的问题就转化成了问题5这样的一个已知问题，体现了数学上的什么思想？

生：化归思想.

设计意图 让学生先对问题6進行观察，为了达到消元的目的，可以对两个方程进行整体的加减，因为相同未知数前面的系数是相同或者互为相反数.从问题5得到启发，引导学生对问题6模仿上述过程解方程，又产生新的追问6.1，6.2，6.3，追问6.3是为了帮助学生进一步理解加减消元法的本质，拓宽思维. 其中几个追问解决之后，就将问题7转化为问题5的类型，通过追问7.4，再次渗透化归思想.

问题7. 问题1、问题2中的未知数的取值分别是什么？

设计意图 单元内容的学习源于问题，学习完之后要回溯本源，解决当初的问题，使之前后照应，不断深化，完整地解决问题.

第5课时

问题8. 三元一次方程组x-y+z=7，①

x+y=-1， ②

2x-y-z=0.③应该如何解？

生：通过消元转化为二元一次方程组来解.

追问8.1：如何消元，选择消哪个未知数？

生：z.

追問8.2：理由是什么呢？

生：因为方程②中不含z，消掉z之后，就可以和②组成二元一次方程组了.

追问8.3：只能先消z吗？

生：不是，消x或者y都可以.

追问8.4：可以如何消？

生：加减或者代入消元法都可以.

设计意图 三元一次方程组课标不做考试要求，但为了进一步让学生体会消元的过程，渗透转化与化归的数学思想，本课直接以解三元一次方程组的问题8引入，激发学生求知欲，引导学生自主探究本题如何进行消元，将解三元一次方程组转化为解二元一次方程组，学会解三元一次方程组的方法. 追问8.1—8.4引导学生加深对消元法的理解与应用，落实能力与素养的培养.

第6课时

问题9. 二元一次方程组解决问题用到的知识有哪些？

问题10. 和一元一次方程解决问题比较有哪些区别与联系？

问题11. 谈谈本单元学习的思路是什么，对研究其他方程有什么启示？

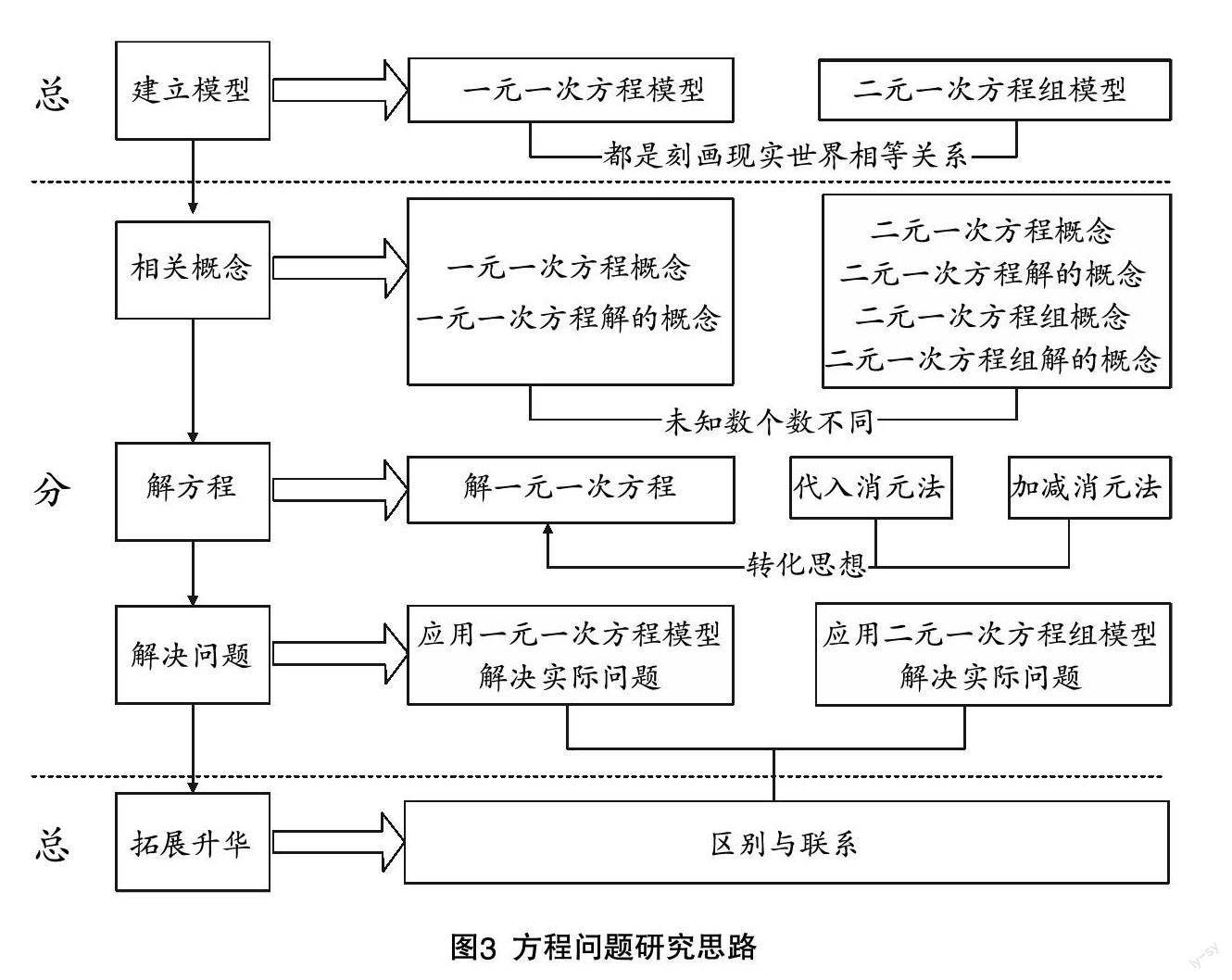
设计意图 本节课是单元教学“总分总”基本路径下的第二个“总”. 问题9目的在于学生学习了本单元所有知识之后，对各部分知识的重新认识与整合，建立知识联结. 问题10、问题11是在问题9的基础上，进一步拓展延伸，将二元一次方程组与一元一次方程有关内容进行深入整合，从而让学生对方程有了更高、更广的认识，从更加系统的角度看待方程问题，形成方程研究思路（如图3）， 提高分析与解决问题的能力，提升数学核心素养.

（四）作业布置

作业是教师为了了解学生学习情况，让学生巩固所学的知识技能与思想方法. 本单元要考查学生是否形成整体研究二元一次方程组的思路，是否体会模型思想与化归思想，因此作业布置要体现出层次性.

层次1：二元一次方程组应用的题目，了解学生对本单元各个内容的掌握情况.

层次2：二元一次方程组的一题多解问题. 在化归思想的引领下，通过不同的方法进行消元，让学生体会不同方法的优劣，检验学生对不同方法的掌握情况，培养学生思维的灵活性.

层次3：让学生自主构造本单元的思维导图，并谈谈学习方程问题的一般思路，以检验学生对本单元内容体系的把握.

层次4：让学生自编二元一次方程组的应用问题. 自编问题要考虑问题情境、二元一次方程组模型、解法（需考虑数据处理）、检验各个步骤.

（五）评价与反馈

单元整体教学视角下对学生学习情况的评价不仅要评价学生对各部分知识的掌握情况，更要关注学生是否形成了整体的系统知识体系，是否领会了其中蕴含的数学思想方法.

参考文献：

［1］ 曾荣. 单元教学的整体设计与课时实施——以“圆锥曲线”单元教学为例［J］. 数学通报，2021，60（03）：33-37.

［2］ 喻平. 数学单元结构教学的四种模式［J］. 数学通报，2020，59（05）：1-8+15.

［3］ 章飞，顾继玲. 单元教学的核心思想与基本路径［J］. 数学通报，2019，58（10）：23-28.

［4］ 中华人民共和国教育部. 义务教育数学课程标准（2011年版）［S］. 北京：北京师范大学出版社，2012.