理解实际意义，培养应用能力

摘要：“王师傅卖鞋问题”的解答情况反映出，当前“有理数的加减法”的教学更多地关注了有理数加减法的法则等纯粹数学知识的学习，而忽略了对有理数和加减法实际意义的理解，没有培养学生应用数学知识解决实际问题的能力。對此，给出三条教学建议：“正数和负数”的教学，要帮助学生体会数学抽象，理解运算对象;“有理数加减运算法则”的教学，要在“同化”与“顺应”中促进学生系统理解算理;“有理数加减法的应用”的教学，要在主客体的变换中帮助学生学会数学建模。

关键词：有理数的加减法;数学抽象;算理;数学建模

本文系江苏省中小学教学研究第十三期立项课题“发展农村初中学生数学建模素养的实践研究”（编号：2019JK13L181）与“农村初中生数学抽象素养培塑的实践研究”（编号：2019JK13L170）的阶段性研究成果。“有理数的加减法”是初中数学最先学习的、最为基本的“数的运算”知识，也是几乎所有学生都能“学好”的知识——各地中考试卷中的相关试题几乎都是“送分题”。但是，学生真的学好“有理数的加减法”了吗？本文通过对“王师傅卖鞋问题”（具体如下）解法与解答情况的分析，试着回答这个问题，并由此谈一谈“有理数的加减法”的教学。

王师傅是卖鞋的，一双鞋进价30元，甩卖20元。一位顾客来买鞋，给了一张50元，王师傅没有零钱，于是找邻居换了50元。事后，邻居发现那一张50元是假币，王师傅又赔了邻居50元。请问：王师傅一共亏了多少钱？

一、解法的分析

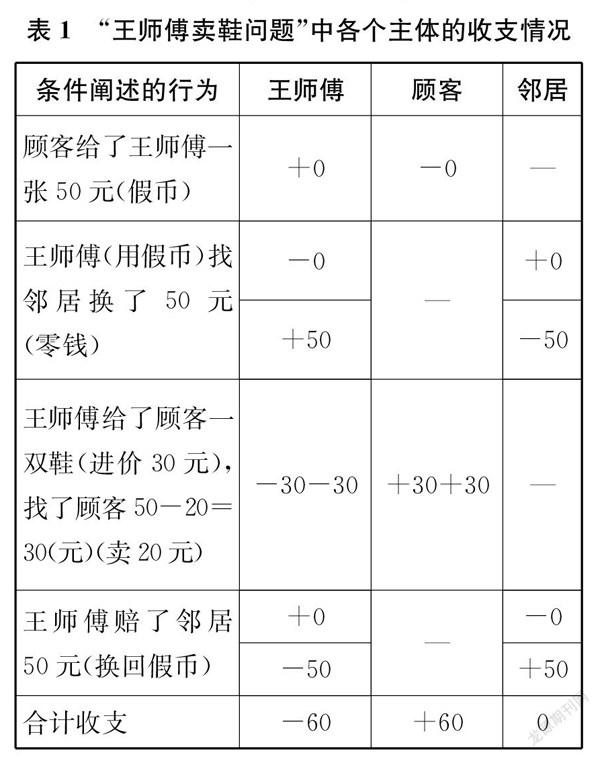
结合有理数（正负数）和加减法的实际意义，可以对这道题的条件做全面的分析。假设收入为正，支出为负，我们可以具体分析条件阐述的每个行为给各个主体带来的收支影响，然后分别将各个主体（只有意义相同的量才可以相加减）的各项收支加起来（因为加的数可以是负数，所以最终的运算包括减法），得到各个主体最终的收支。分析的过程和结果如表1所示（其中，假币的价值是0）。

由此，在题目只要求王师傅一共亏了多少钱的情况下，完整的列式解法（解法1）是0-0+50-30-30+0-50=-60（元）。在此，若不考虑收支假币以及抵消对邻居的收支，则节约（缩略）的列式解法（解法2）是-30-30=-60（元）。当然，若假设支出为正，则是30+30=60（元）;若转换考虑顾客的收入就是王师傅的支出（因为邻居收支相抵），则也是30+30=60（元）。以上式子中的一个“30”也都可以写成“50-20”。

此外，还有一种统整考虑的解法（解法3）：收到假币亏50元（买卖需要用同等价值物品和找钱交换），卖出一双鞋子亏30-20=10（元）（低于进价甩卖本身要亏本），因此解法是50+10=60（元）。这里的“10”也可以写成“30-20”。

可见，解决这道题需要运用的，主要不是有理数加减法的法则，而是有理数和加减法的实际意义。进一步来看，这道题考查的并不是纯粹的数学知识（用到的数学知识非常简单），而是应用数学知识解决实际问题的能力。

首先，解决本题时，要将实际问题抽象为“互为相反意义的量”的数学问题。如果能正确地用“正负数”来表示，那么，列式将更简单，只需要考虑加法（求代数和）。当然，如果没有学过“正负数”，只要理解实际意义，也可很方便地用加减混合运算（求绝对值的和或差）解决本题。

其次，解决本题时，准确理解运算的对象，即参与运算的所有数据的实际意义，尤其重要。其实，从下文解答情况的分析中，我们可以发现，解决本题时没有因为“数值运算”出错的，都是因为“意义运算”出错的，即对意义不同（如行为主体不同、收支方向不同）或对意义有重复、遗漏情况的数据进行加（减）法运算。

再次，解决本题时，要选择合适的对象（王师傅、顾客、邻居）进行分析，得出如“王师傅的支出-王师傅的收入=王师傅亏的”“顾客的收入-顾客的支出=顾客赚的”“三个人中，一些人赚的=另一些人亏的（系统收支平衡，没有外部收支）”“邻居不赚不亏，所以，王师傅亏的=顾客赚的”等模型，然后选择适当的模型列式运算。

二、三个群体解答情况的分析

这道题曾经以多种版本在网络上流传，成为一些数学教师以及数学爱好者甚至全民用来检测智力水平的热题。笔者曾经参与某知名数学教师QQ群对本题的讨论，并利用本题在笔者所任教的七年级学生中进行测试，还在笔者所指导的数学师范生中进行调查。下面简述不同群体对本题的解答情况。

数十位教师参与了QQ群里的讨论，分别来自5个省的8个地级市的10多位教师做了有效发言。笔者将他们对本题的解答情况做了整理、统计，得到表2（表中的“算式含义解释”是教师给出的，不是笔者推测的）。可见，教师的结果正确率大概是30%，过程正确率大概是20%。

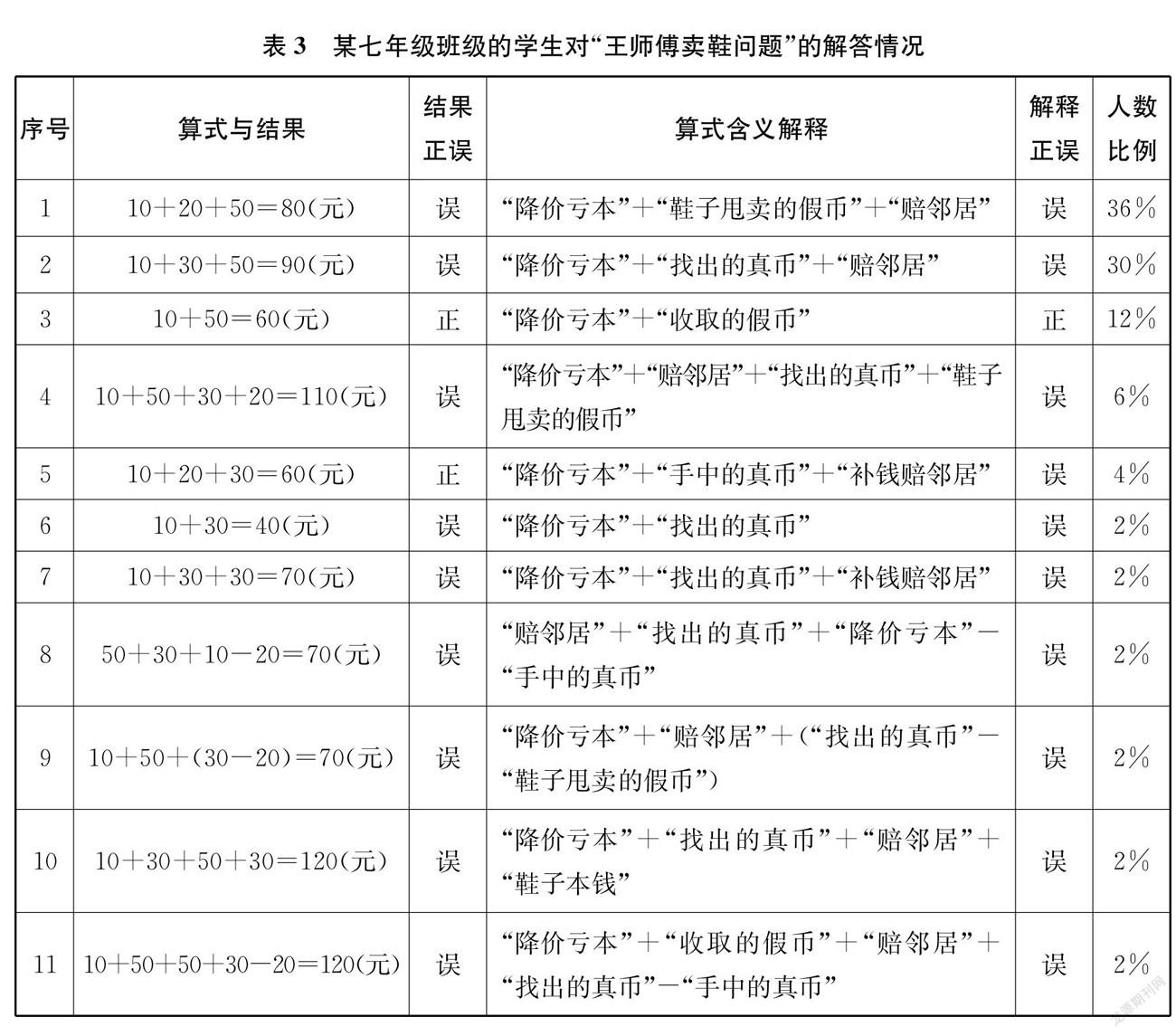
在七年级上学期第一节数学课上，笔者对尚未学习“有理数的加减法”的学生进行了测试。他们对本题的解答情况如下页表3所示（表中的“算式含义解释”是学生给出的，不是笔者推测的）。可见，学生的结果正确率大概是16%，过程正确率大概是12%。

在为两所大学数学教育（师范）专业本科生做教学实践指导方面的报告的过程中，笔者曾经利用本题做了调查。因为是现场调查，不便了解观众的思维过程，所以，只统计了结果正确率。结果，一所学校将近60名师范生的正确率竟然为0，另一所学校将近80名师范生的正确率也不足30%，而两所学校统算的正确率只有17%。

综上，解答本题时，教师（在职教师）、师范生（未来教师）和七年级新生的正确率都很低。而绝大部分错误都是因为所列算式（所做运算）没有实际意义（其中有些量不能相加减）。这充分说明了，很多的“有理数的加减法”教学，更多地关注了有理数加减法的法则等纯粹数学知识的学习，而忽略了有理数和加减法实际意义的理解，没有培养学生应用数学知识解决实际问题的能力。

三、对“有理数的加减法”教学的启示

通过对以上案例的分析，我们不难发现，“有理数的加减法”的教学，特别要注意帮助学生理解有理数和加减法的实际意义，培养学生应用数学知识解决实际问题的能力。为此，要做好以下几点：

（一）“正數和负数”的教学：帮助学生体会数学抽象，理解运算对象

有理数的加减法与小学的正数加减法主要的区别在于引入了“负数”的概念。这就使得学生在理解运算对象，尤其是复杂情境中的运算对象时，容易产生混乱。所以，正负数的概念是有理数加减法的知识起点，要真正学好有理数的加减法必须先学好正负数的概念。

1.注重正负数概念的形成性，帮助学生体会数学抽象

在实际教学中，正负数的概念并未得到应有的重视。不少初中教师因为学生在小学已经学过正负数，所以在教学中一带而过，使得不少学生只是通过少量特征明显的实例就抽象出正负数的概念，缺乏从较为复杂的情境中抽象正负数概念的经历，从而导致在面临具体问题时，没有使用正负数解决问题的意识，或不能正确地使用正负数表征问题。事实上，根据笔者事后的访谈，解决本题时，有意识地使用正负数知识的人不到20%，大部分人的解法停留在正数运算层面。可见，在“正数和负数”的教学中，教师不但要揭示概念的形成过程，而且要让学生参与到概念的生成过程中;既要提供大量正负数的实例让学生提炼、抽象，还要让学生举出（或制造）大量的实例以加深理解。

2.揭示正负数概念的相对性，帮助学生理解运算对象

数学运算素养主要表现为“理解运算对象，掌握运算法则，探究运算思路，求得运算结果”。在实际教学中，教师往往对“掌握运算法则，探究运算思路，求得运算结果”关注较多，而对“理解运算对象”关注不够。表现在上述案例中，就是计算的结果正确，但是所列算式却不完全正确。在正负数概念的教学中，教师往往只强调正负数的“绝对性”，而忽略正负数的“相对性”。具体到本题中，所谓的“绝对性”是指将“盈利为正”“亏损为负”绝对化地作用于单一对象（如王师傅），缺乏变通理解。所谓的“相对性”是指同一个数据对不同的对象有不同的意义，也就是可以有不同的正负性（如表1中各行所示）。所以，在正负数概念的教学中，教师要通过实例让学生理解正负数的“绝对性”和“相对性”之间的相互依存关系，帮助学生理解运算对象。

（二）“有理数加减运算法则”的教学：在“同化”与“顺应”中促进学生系统理解算理

在“有理数的加减法”的教学中，多数教师都明白小学的正数加减法是有理数加减法的基础，正数范围内的运算法则与运算律在有理数范围内仍然适用，知道用正数的加减法“同化”有理数的加减法，但是，缺少对正数的加减法也符合有理数的加减法所有规则的“顺应”过程的分析。这种只强调“同化”、不强调“顺应”的做法，会使学生原有的知识与新学的知识难以衔接，导致学生难以站在更高的角度理解旧知、接受新知，更有甚者会因为只强调“同化”而变得因循守旧、不思创新。所以，在教学过程中，既要用原有的知识“同化”新的问题，更要让原有的方法“顺应”新的情况，保证运算法则前后的一致性。只有这样，才能使学生对所学运算法则知其然并知其所以然，获得对运算法则较为系统的理解。最后再提及一点，不少学生在解决相关问题时一律回到小学的正数加减知识和方法上，就是因为“顺应”工作没有做好。

（三）“有理数加减法的应用”的教学：在主客体的变换中帮助学生学会数学建模

教学“有理数加减法的应用”时，教师通常设置单一主体的问题情境。比如，“出租车行驶位置问题”和“出租车油耗问题”，前者只需求代数和，后者只需求绝对值的和，两者都只要关注一个变量。这种单一主体的问题训练多了，学生很容易被“套路”，形成套题型的习惯。所以，我们应该设置适当难度的多个主体的问题情境，让学生在多个主体的转换中理解同一个数据的不同意义，从而真正理解运算对象，学会选择合适的主体，建立恰当的数学模型（数量关系），较为便捷地解决问题。

一个典型的例子是：

小明向妈妈借500元钱，向爸爸借500元钱，一共得到1000元。自己买了一双鞋，花了970元，手头还有30元;先还妈妈10元，再还爸爸10元，手中还剩10元。这样，还欠妈妈490元，还欠爸爸490元，欠妈妈和爸爸的钱加起来是980元，加上自己还剩的10元一共是990元。问：还有10元钱哪儿去了？

对于此题，只有厘清了各个数据对应的主体和客体，才能选择合适的主体进行研究，准确理解每一个数据的意义，赋予每一个数据正确的符号，从而理解问题中的“490+490+10=990”这个算式是没有实际意义的，其原因是式子的左边不是同一性质的数据，不可以用绝对值相加。进而知道，本题应该用“个人资产=债务（负数）+债权（正数）+现金（正数）+实物价值（正数）”这个模型来计算。这样，妈妈的资产是490（债权）+10（现金）=500（元），爸爸的资产也是490（债权）+10（现金）=500（元），也就是说，爸爸和妈妈的资产还是每人500元，一共1000元，只不过是形式发生了变化，各自有490元从现金变为了债权;小明的资产是-490（对妈妈的债务）-490（对爸爸的债务）+10（现金）+970（鞋的价值）=0，也就是说，小明尽管有980元的债务，同时还有10元现金和价值970元的鞋，所以实际资产还是0元，并没有变化。由此，从每个人的角度看，都不存在资产矛盾，所以，题目所问的“还有10元钱哪儿去了？”是一个不存在的问题。

参考文献：

[1] 徐小建.例谈数学建模素养的落实——以“胡不归”问题的教学为例[J].中小学教材教学，2019（4）.

[2] 徐小建.基于“数学抽象”素养的函数概念生成教学[J].中小学教材教学，2020（11）.